Thanks for taking the time to think about this! But it seems to me that Löb's theorem should not be required to prove proposition 3 for a properly defined A. I'm guessing that you inadvertently defined A asymmetrically, as described in "AI cooperation in practice", instead of the symmetric way described in "model of UDT with a halting oracle" where swapping C and D shouldn't affect anything except the chicken stage.
Ah, I see. The agent described in "A model of UDT with a halting oracle" is more symmetric, because it has a choice of three actions: "Cooperate", "Defect", and "Break down and cry" (if we count failing to act as an action).
I think I see a way to prove the proposition without using Löb's theorem, and I don't even need to change the definition of A. I'll post here whether it works out.
Thanks for the comment!
I only looked at this for a bit so I could be totally mistaken, but I'll look at it closely soon, it's a nice write up!
My thoughts:
A change of variables/values in your proof of proposition 3 definitely doesn't yield conjecture 4? At first glance it looks like you could just change the variables and flip the indicies for the projections (use pi_1 instead of pi_0) and in the functions A[U,i]. If you look at the U() defined for conjecture 4, it's exactly the one in proposition 3 with the indices i flipped and C and D flipped, so it's surprising to me if this doesn't work or if there isn't some other minor transformation of the the first proof that yields a proof of conjecture 4.
The agent function is not defined symmetrically with respect to C and D, so flipping the roles of C and D in the universe without also flipping their roles in the agent function does not guarantee that the outcome would change as desired.
Yes, you're right. Looking at the agent function, the relevant rule seems to be defined for the sole purpose of allowing the agent to cooperate in the even that cooperation is provably better than than defecting. Taking this out of context, it allows the agent to choose one of the actions it can take if it is provably better than the other. It seems like the simple fix is just to add this:
=D\to\pi_{\underline{i}}\chi()=\underline{a})\\\mbox{\quad\quad\quad\quad}\wedge(\psi(\ulcorner%20U%20\urcorner,\underline{i})=C\to\pi_{\underline{i}}\chi()=\underline{b})\biggr)\wedge%20a%20%3E%20b)
If you alter the agent definition by replacing the third line with this and the fourth with C you have an agent that is like the original one but can be used to prove conjecture 4 but not prop 3, right? So if you instead add this line to the current agent definition and simply leave D as the last line, then if neither the old third line nor this new one hold we simply pick D, which is neither provably better nor provably worse than C, so that's fine. It seems that we can also prove conjecture 4 by using the new line in lieu of the old one, which should allow us to use a proof that is essentially symmetric to the proof of proposition 3.
Does that seem like a reasonable fix?
So you modify the agent so that line 3 says "cooperating is provably better than defecting" and line 4 says "defecting is provably better than cooperating". But line 3 comes before line 4, so in proving Conjecture 4 you'd still have to show that the condition in line 3 does not obtain. Or you could prove that line 3 and line 4 can't both obtain; I haven't figured out exactly how to do this yet.
Well the agent definition contains a series of conditionals. You have as the last three lines: if "cooperating is provably better than defecting", then cooperate; else, if "defecting is provably better than cooperating" then defect; else defect. Intuitively, assuming the agent's utility function is consistent, only one antecedent clause will evaluate to true. In the case that the first one does, the agent will output C. Otherwise, it will move through to the next part of the conditional and if that evaluates to true the agent will output D. If not, then it will output D anyway. Because of this, I would go for proving that line three and 4 can't both obtain.
Or you could prove that line 3 and line 4 can't both obtain; I haven't figured out exactly how to do this yet.
How about this? Suppose condition 3 and 4 both obtain. Then there exists and a and b such that U(C) = #a and U(D) = #b (switching out the underline for '#'). Also, there exists a p and q such that p > q and U(D) = #p and U(C) = #q. Now U(C) = #a > #b = U(D) = #c > #q = U(C) so U(C) > U(C). I may actually be confused on some details, since you indicate that a and b are numbers rather than variables (for instance in proposition 2 you select a and b as rational numbers), yet you further denote numerals for them, but I'm assuming that a >b iff #a > #b. Is this a valid assumption? I feel as though I'm missing some details here, and I'm not 100% sure how to fill them in. If my assumption isn't valid I have a couple of other ideas. I'm not sure if I should be thinking of #a as 'a' under some interpretation.
Going a little bit further, it looks like your lemma 1 only invokes the first two lines and can easily be extended for use in conjecture 4 - look at parts 1 and 3. Part 1 is one step away from being identical to part 3 with C instead of D.
~Con(PA) -> ~ Con(PA + anything), just plug in Con(PA) in there. Adding axioms can't make an inconsistent theory consistent. Getting the analogous lemma to use in conjecture 4 looks pretty straightforward - switching out C with D and vice versa in each of the parts yields another true four part lemma, identical in form but for the switched D's and C's so you can use them analogously to how you used the original lemma 1 in the proof of proposition 3.
One can try to take the proof of Proposition 3 and switch C and D around, but one quickly runs into difficulty: The second line of that proof contains
%20=%20C%20\to%20\pi_0%20U()%20=%20\underline{a}%20)%20\\%20\mbox{\quad\quad\quad\quad}%20\wedge%20(A(\ulcorner%20U%20\urcorner,%200)%20=%20D%20\to%20\pi_0%20U()%20=%20\underline{b})%20\biggr)%20\wedge%20a%3Eb)
"cooperating provably results in a better payoff than defecting". This is enough to convince the agent to cooperate. But if you switch C and D, you end up with a proposition that means "cooperating provably results in a worse payoff than defecting". This is not enough to convince the agent to defect. The agent will defect if there is no proof that cooperating results in a better payoff than defecting. So at least one would have to say a bit more here in the proof.
Briefly, is a variable, while
is a numeral — i.e., the string
where
occurs x times. I just learned that the standard notation is not
but
.
Less briefly: As I say in this comment, when I write ), what I really ought to write is
)), where
) interprets z as the Gödel number of a string of symbols and replaces every occurrence of the first free variable with the string 1+...+1, where 1 occurs x times.
Your work is wrong. To apply diagonal lemma the definition of phi must be a formula, since you write |- (which is not a formula in PA) I assume you meant it as shorthand for Godels Bew (which is), but you can't existentially quantify Bew like you did in line 3 of the definition.
"Your work is wrong" is an unfair characterization of presence of a minor technical inaccuracy.
Yes, I really mean phi to be a formula based on the provability predicate. The third line is really shorthand for
))
where Sub is a function that replaces the first two free variables in the Gödelized formula with a and b. So we can quantify over a and b.
I suppose I should mention this in the post.
I'm not mathy enough to understand this post, but...
- Thanks for going to all this trouble! Hopefully those more mathy than I can check your work and extend it.
- Nice title.
It's awesome of you to write this up! I'm going to have to look through it more carefully tomorrow.
One idea I take out of your definition of A is that it's potentially useful to think about decisions as giving "strategies" that respond not just to "observations" (that were "withheld" during a decision), but also to "observations about utility", that could factor out the differences between different agents and allow them to coordinate, the way a single agent can coordinate with its copies or counterfactual variants by deciding on a whole strategy instead of just a single action. Not sure if (or how) that works for PD though...
Proof of Proposition 3 (without using Löb's theorem). This proof uses Lemma 6.
For brevity, let stand for
), let
stand for
), and let
) stand for
%20\wedge%20(A_i%20=%20D%20\to%20U_i%20=%20b)).
First, notice that
%0A\\%20\vee%20&%20(a%20\neq%20-1%20\wedge%20a%20\neq%201)%0A\\%20\vee%20&%20(b%20\neq%200%20\wedge%20b%20\neq%202)%0A\end{array}%0A\\&\to%20\begin{array}[t]{r@{\,}ll}%0A&%20\operatorname{Prv}(%20\dot{a}%20=%201%20\wedge%20\dot{b}%20=%200)%20&%20\mbox{by%20Lemma%206(b),(f)}%0A\\%20\vee%20&%20\operatorname{Prv}(\dot{a}%20\neq%20-1%20\wedge%20\dot{a}%20\neq%201)%20&%0A\\%20\vee%20&%20\operatorname{Prv}(%20\dot{b}%20\neq%200%20\wedge%20\dot{b}%20\neq%202))%20&%0A\end{array}%0A\end{align*})
So
)%20\vdash%20A_0%20=%20C%20\to)
)%20\wedge%20a%20%3E%20b)%20&%0A\\&\to%20\exists%20a,b%20(\begin{array}[t]{r@{\,}l}%0A&\operatorname{Prv}(%20\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}=1%20\wedge%20\dot{b}%20=%200)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}%20\neq%20-1%20\wedge%20\dot{a}%20\neq%201)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{b}%20\neq%200%20\wedge%20\dot{b}%20\neq%202))%0A\end{array}%20&%0A\\&\to%20\exists%20a,b%20(%20\begin{array}[t]{r@{\,}l}%0A&%20\operatorname{Prv}((A_0%20=%20C%20\to%20U_0%20=%201)%20\wedge%20(A_0%20=%20D%20\to%20U_0%20=%200))%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20=%20C%20\to%20U_0%20\neq%20-1%20\wedge%20U_0%20\neq%201)%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20=%20D%20\to%20U_0%20\neq%200%20\wedge%20U_0%20\neq%202))%0A\end{array}%20&%20\mbox{by%20definition%20of%20}%20\phi_0%0A\end{align*})
%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20D))%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20=%20C\to%20\bot)%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20=%20D\to%20\bot)%0A\end{array}%20&%0A\\&\to%20\begin{array}[t]{r@{\,}l}%0A&%20\operatorname{Prv}(A_0%20=%20A_1)%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20\neq%20C)%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20\neq%20D)%0A\end{array}%20&%0A\\&\to%20\operatorname{Prv}(A_0%20=%20A_1)%20&%20\mbox{by%20Lemma%201.1,3}%0A\\&\to%20\operatorname{Prv}(\phi_0(1,0))%20&%0A\\&\to%20\exists%20a,b%20\operatorname{Prv}(\phi_1(\dot{a},\dot{b}))%20\wedge%20a%3Eb%20&%0A\\&\to%20A_1%20=%20C%0A\end{align*})
Similarly,
)%20\vdash%20A_1%20=%20C%20\to%20A_0%20=%20C)
So
)%20\vdash%20A_0%20=%20A_1)
So
%0A\\%20\vee%20&%20(%20\operatorname{Con}(\operatorname{PA})%20\wedge%20\neg%20\operatorname{Con}(\operatorname{PA}%20+%20\operatorname{Con}(\operatorname{PA})))%20%0A\\%20\vee%20&%20(\operatorname{Con}(\operatorname{PA}%20+%20\operatorname{Con}(\operatorname{PA}))%20\wedge%20A_0%20=%20A_1)%0A\end{array}%20&%0A\\%20&%20\vdash%20\begin{array}[t]{r@{\,}l}%0A&%20A_0%20=%20D%20=%20A_1%0A\\%20\vee%20&%20A_0%20=%20C%20=%20A_1%0A\\%20\vee%20&%20A_0%20=%20A_1%0A\end{array}%20&%20\mbox{by%20Lemma%201.2,4}%0A\\%20&%20\vdash%20A_0%20=%20A_1%0A\\%20&%20\vdash%20\phi_0(1,0)%0A\end{align*})
So there exist natural numbers and
such that
)%20\wedge%20a%3Eb) is true. Therefore, assuming consistency of
), by the definition of
, we have
. Similarly,
.
Proof of Proposition 4. This is kinda similar to the new proof of Proposition 3. It uses Lemma 6.
)%20\vdash%20A_0%20=%20C%20\to)
)%20\wedge%20a%20%3E%20b)%20&%0A\\&\to%20\exists%20a,b%20(\operatorname{Prv}(\phi_0(\dot{a},\dot{b}))%20\wedge%20(%20\begin{array}[t]{r@{\,}l}%0A&%20(a%20\neq%200%20\wedge%20a%20\neq%202)%0A\\%20\vee%20&%20(b%20\neq%20-1%20\wedge%20b%20\neq%201)%0A\\%20\vee%20&%20(a%20=%200%20\wedge%20b%20=%20-1)%0A\\%20\vee%20&%20(a%20=%202%20\wedge%20b%20=%201)%0A\\%20\vee%20&%20(a%20=%202%20\wedge%20b%20=%20-1)))%0A\end{array}%20&%0A\\&\to%20\exists%20a,b%20(%20\begin{array}[t]{r@{\,}l}%0A&%20\operatorname{Prv}(%20\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}%20\neq%200%20\wedge%20\dot{a}%20\neq%202)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{b}%20\neq%201%20\wedge%20\dot{b}%20\neq%201)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}%20=%200%20\wedge%20\dot{b}%20=%20-1)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}%20=%202%20\wedge%20\dot{b}%20=%201)%0A\\%20\vee%20&%20\operatorname{Prv}(\phi_0(\dot{a},\dot{b})%20\wedge%20\dot{a}%20=%202%20\wedge%20\dot{b}%20=%20-1))%0A\end{array}%20&%20\mbox{by%20Lemma%206(b),(f)}%0A\end{align*})
%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20\neq%20D)%0A\\%20\vee%20&%20\operatorname{Prv}((A_0%20=%20C%20\to%20A_1%20=%20C)%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20C))%0A\\%20\vee%20&%20\operatorname{Prv}((A_0%20=%20C%20\to%20A_1%20=%20D)%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20D))%0A\\%20\vee%20&%20\operatorname{Prv}((A_0%20=%20C%20\to%20A_1%20=%20D)%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20C)))%0A\end{array}%20&%0A\end{align*})
%0A\\%20\vee%20&%20\operatorname{Prv}(A_0%20\neq%20D)%0A\\%20\vee%20&%20\operatorname{Prv}(A_1%20=%20C)%0A\\%20\vee%20&%20\operatorname{Prv}(A_1%20=%20D)%0A\\%20\vee%20&%20\operatorname{Prv}((A_0%20=%20C%20\to%20A_1%20=%20D)%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20C))%0A\end{array}%20&%0A\\&\to%20\operatorname{Prv}((A_0%20=%20C%20\to%20A_1%20=%20D)%20\wedge%20(A_0%20=%20D%20\to%20A_1%20=%20C))%20&%20\mbox{by%20Lemma%201.1,3}%0A\\&\to%20\operatorname{Prv}((A_1%20=%20C%20\to%20A_0%20=%20D)%20\wedge%20(A_1%20=%20D%20\to%20A_0%20=%20C))%20&%0A\\&\to%20\operatorname{Prv}((A_1%20=%20C%20\to%20U_1%20=%202)%20\wedge%20(A_1%20=%20D%20\to%20U_1%20=%20-1))%20&%0A\\&\to%20\exists%20a,b%20(\operatorname{Prv}(\phi_1(\dot{a},\dot{b}))%20\wedge%20a%3Eb)%20&%0A\\&\to%20A_1%20=%20C%20&%0A\end{align*})
Similarly,
)%20\vdash%20A_1%20=%20C%20\to%20A_0%20=%20C)
So
)%20\vdash%20A_0%20=%20A_1)
So
%0A\\%20\vee%20&%20(\operatorname{Con}(\operatorname{PA})%20\wedge%20\neg%20\operatorname{Con}(\operatorname{PA}%20+%20\operatorname{Con}(\operatorname{PA})))%20%0A\\%20\vee%20&%20(\operatorname{Con}(\operatorname{PA}%20+%20\operatorname{Con}(\operatorname{PA}))%20\wedge%20A_0%20=%20A_1)%0A\end{array}%20&%20\mbox{by%20definition%20of%20}%20A%0A\\%20&%20\vdash%20\begin{array}[t]{r@{\,}l}%0A&%20A_0%20=%20D%20=%20A_1%0A\\%20\vee%20&%20A_0%20=%20C%20=%20A_1%0A\\%20\vee%20&%20A_0%20=%20A_1%0A\end{array}%20&%20\mbox{by%20Lemma%201.2,4}%0A\\%20&%20\vdash%20A_0%20=%20A_1%20&%0A\\%20&%20\vdash%20\phi_0(0,1)%20&%0A\end{align*})
Suppose also that ) for some
and some
. Then
%20\wedge%20\phi_0(\dot{a},%20\dot{b})%0A\\&%20\vdash%20(A_0%20=%20C%20\to%20U_0%20=%200)%20\wedge%20(A_0%20=%20C%20\to%20U_0%20=%20\dot{a})%0A\\&%20\vdash%20A_0%20=%20C%20\to%200%20=%20U_0%20=%20\dot{a}%0A\\&%20\vdash%20A_0%20=%20C%20\to%20\bot%0A\\&%20\vdash%20A_0%20\neq%20C%0A\end{align*})
Assuming consistency of ), this is impossible by Lemma 1.3. So if
), then
must be
. Similarly, one can prove that
must be
. Thus, assuming consistency of
),
)%20\wedge%20a%20%3E%20b))
So, by the definition of , we have
. Similarly,
.
Here's my meager attempt at contribution. And my apologies for not knowing LaTeX.
if exists a,b: provable([A(U,i)=C implies pi(i)(U())=a] and [A(U,i)=D implies pi(i)(U())=b] and [a>b]):
C
else:
D
You can do a lot better than this. Consider, for instance:
if exists a: provable([A(U,i)=C implies p(i)(U())>=a] and [A(U,i)=D implies pi(i)(U())<=a]):
C
else:
D
Consider the set S of all sets S(k) such that provable(A(U,i)=C implies pi_i(U()) is in S(k)). Then A(U,i)=C implies pi_i(U()) is in intersection(S). I don't know much about formal arithmetic, so I couldn't say whether it is necessary true that provable(A(U,i)=C implies pi(i)(U()) is in intersection(S)). But if that is true, then intersection(S)) is in S, and thus there exists a unique most specific S(k) such that provable(A(U,i)=C implies pi(i)(U()) is in S(k)). If it is possible in formal arithmetic to identify this set, then you can establish a utility function over such minimal sets of possible values of pi(i)(U()) implied by A(U,i)=C. For example, if that set is finite, the its utility could just be the average of its members. And then you could do the same sort of thing for A(U,i)=D and compare the utilities of the resulting sets of possibilities. This would essentially give you a single utility value for each choice, and you wouldn't get stuck if you can't prove that each output of A implies some unique value of pi(i)(U()).
What is the correct generalization of that can choose between n actions, and not just two? How about infinitely many actions?
For finite sets of actions, one possibility is that you can compare every pair of actions, giving you a partial ordering of the set, and then you could choose a maximal element. Alternatively, if my earlier idea for improving on the comparisons works, you can assign a utility to each possible action, so you can just choose the best one. If you have infinitely many possible actions, this will of course give you problems, since it can turn into a "name the biggest number" contest.
Note that we are intending to talk about agents that optimize over how U() works, but your framework also allows the creation of agents that optimize over how pi(i)(_) works. For instance, consider the following scenario:
U(): return (0, 0)
pi(i)(a,b): return 1 if A(U,i)=C, else 0
In this case, A(U,i) would output C, but not because it would imply anything about U. It might make sense to have some computability restriction on pi so that all such agents will actually be optimizing the world function rather than their own utility functions.
Proof of Proposition 6. This proof uses Fact 5, the converse Barcan formula.
Strictly speaking, variables in Peano arithmetic are supposed to refer to natural numbers, and axioms like reflect this. But in this post, we have been treating variables like rational numbers! In fact, there are ways of talking about rational numbers using Peano arithmetic, and so far in this post we haven't bothered to write them out. But for this proof it will be important to distinguish between naturals and rationals. First we'll prove literal readings of (a) - (e) — that is, we'll assume variables refer to natural numbers. Then we'll indicate how to extend the proofs to rational versions of the Lemma.
(a)
%20\to%20Q(x_1,%20\dots,%20x_k))%20&%0A\\&%20\vdash%20\operatorname{Prv}(\forall%20x_1,%20\dots,%20x_k%20(P(x_1,%20\dots,%20x_k)%20\to%20Q(x_1,%20\dots,%20x_k)))%20&%0A\\&%20\vdash%20\forall%20x_1,%20\dots,%20x_k%20\operatorname{Prv}(P(\dot{x}_1,%20\dots,%20\dot{x}_k)%20\to%20Q(\dot{x}_1,%20\dots,%20\dot{x}_k))%20&%20\mbox{(converse%20Barcan%20formula)}%0A\\&%20\vdash%20\forall%20x_1,%20\dots,%20x_k%20\operatorname{Prv}(P(\dot{x}_1,%20\dots,%20\dot{x}_k))%20\to%20\operatorname{Prv}(Q(\dot{x}_1,%20\dots,%20\dot{x}_k))%20&%0A\end{align*})
(b)
%20&%0A\\&%20\vdash%20\forall%20x%20\operatorname{Prv}(\dot{x}%20=%20\dot{x})%20&%20\mbox{(converse%20Barcan%20formula)}%0A\\&%20\vdash%20\forall%20x%20\operatorname{Prv}(\operatorname{Sub}(\ulcorner%20x%20=%20x%20\urcorner,%20x))%20&%0A\\&%20\vdash%20\forall%20x%20\operatorname{Prv}(\operatorname{Sub}(\ulcorner%20x%20=%20y%20\urcorner,%20x,%20x))%20&%0A\\&%20\vdash%20\forall%20x,%20y%20(%20x%20=%20y%20\to%20\operatorname{Prv}(\operatorname{Sub}(\ulcorner%20x%20=%20y%20\urcorner,%20x,%20y)))%20&%0A\\&%20\vdash%20\forall%20x,%20y%20(x%20=%20y%20\to%20\operatorname{Prv}(\dot{x}%20=%20\dot{y}))%20&%0A\end{align*})
(c) Starting from the fourth line in the proof of (b),
)%0A\\&%20\vdash%20\forall%20x,y%20\operatorname{Prv}(\operatorname{Sub}(\ulcorner%20z%20=%20z%20\urcorner,%20x%20+%20y))%0A\\&%20\vdash%20\forall%20x,y%20\operatorname{Prv}(\operatorname{Concat}(\operatorname{Sub}(\ulcorner%20z%20\urcorner,%20x%20+%20y),%20\ulcorner%20=%20\urcorner,%20\operatorname{Sub}(\ulcorner%20z%20\urcorner,%20x%20+%20y))%0A\end{align*})
is a recursive function such that
%20=%20\ulcorner%20\alpha%20\beta%20\gamma%20\urcorner). Now by messing around with Gödel numbers and numerals, one can prove
%20=%20\operatorname{Sub}(\ulcorner%20x%20+%20y%20\urcorner,%20x,%20y))
so
,%20\ulcorner%20=%20\urcorner,%20\operatorname{Sub}(\ulcorner%20x%20+%20y%20\urcorner,%20x,%20y)))%0A\\&%20\vdash%20\forall%20x,y%20\operatorname{Prv}(\dot{x%20+%20y}%20=%20\dot{x}%20+%20\dot{y})%0A\end{align*})
(d) We proceed by induction on . The base case:
%20&%0A\\&%20\vdash%20\forall%20x%20\operatorname{Prv}(%200%20=%20\dot{x}%20\times%200)%20&%20\mbox{(converse%20Barcan%20formula)}%0A\\&%20\vdash%20\forall%20x%20\operatorname{Prv}(%20\dot{\overbrace{x%20\times%200}}%20=%20\dot{x}%20\times%200)%20&%0A\end{align*})
Now for the induction step, which implicitly uses part (a) in almost every step:
%20\to%20\operatorname{Prv}(\dot{\overbrace{x(y+1)}}%20&%20=%20\dot{\overbrace{xy%20+%20x}}%20&%0A\\&%20=%20\dot{\overbrace{xy}}%20+%20\dot{x}%20&%20\mbox{by%20(c)}%0A\\&%20=%20\dot{x}%20\times%20\dot{y}%20+%20\dot{x}%20&%0A\\&%20=%20\dot{x}%20\times%20(\dot{y}%20+%201)%20&%0A\\&%20=%20\dot{x}%20\times%20\dot{\overbrace{y%20+%201}}%20)%20&%20\mbox{%20by%20(c)}%0A\end{align*})
(e)
%20&%20\mbox{by%20(b)}%0A\\&%20\to%20\exists%20z%20\operatorname{Prv}(%20\dot{x}%20=%20\dot{y}%20+%20\dot{z}%20+%201)%20&%20\mbox{by%20(c)}%0A\\&%20\to%20\exists%20z%20\operatorname{Prv}(%20\dot{x}%20%3E%20\dot{y})%20&%0A\\&%20\to%20\operatorname{Prv}(%20\dot{x}%20%3E%20\dot{y})%0A\end{align*})
Now we consider rational numbers. Every rational number can be written as
where and
are natural numbers. So one way to represent a rational-valued variable in Peano arithmetic is with a triple
) of natural-valued variables. Two rational numbers are equal to each other when
Rearranging, we get
This condition is expressible in Peano arithmetic, and is how we can express equality of two rationals.
We can prove a rational version of (b) using the natural version of (b) and repeated application of the natural versions of (c) and (d):
%20&%20%0A\\%20&%20\to%20\operatorname{Prv}(\dot{x}%20\times%20\dot{y}''%20+%20\dot{x}%20+%20\dot{y}'%20\times%20\dot{x}''%20+%20\dot{y}'%20=%20\dot{y}%20\times%20\dot{x}''%20+%20\dot{y}%20+\dot{x}'%20\times%20\dot{y}''%20+%20\dot{x}')%20&%20%0A\end{align*})
With similar strategies one can prove rational versions of (a), (c), (d), and (e). Then we can prove the rational version of (f) directly:
(f)
%20\vee%20\operatorname{Prv}(\dot{y}%20%3E%20\dot{x})%20&%20\mbox{by%20(e)}%0A\\&\to%20\operatorname{Prv}(\dot{x}%20\neq%20\dot{y})%20\vee%20\operatorname{Prv}(\dot{y}%20\neq%20\dot{x})%20&%0A\\&\to%20\operatorname{Prv}(\dot{x}%20\neq%20\dot{y})%0A\end{align*})
Fact 5 (Converse Barcan formula). For every formula ) with one free variable,
)%20\to%20\forall%20x%20\operatorname{Prv}(\phi(\dot{x}))).
(The formula )) is shorthand for
%20\urcorner,%20x))). Whenever a free variable appears inside the
predicate, there's an implicit
predicate there. I'm using a dot instead of an underline now.)
This fact is the converse of the Barcan formula in quantified provability logic. I'm not going to prove this, because it would be tedious and it would depend on the exact definition of , which I want to avoid in this post. Fact 5 is asserted without proof here, and Boolos[1] asserts it with barely more than no proof.
The converse Barcan formula implies some theorems of the form %20\to%20\operatorname{Prv}(\phi(\dot{x})))). This doesn't work for all predicates
) — for example, take
) to be a sentence that is true for the natural numbers but not provable. Here are the theorems we will need:
Lemma 6.
(a) If %20\to%20Q(x_1,%20\dots,%20x_k))),
then )%20\to%20\operatorname{Prv}(Q(\dot{x}_1,%20\dots,%20\dot{x}_k))))
(b) ))
(c) )
(d) )
(e) ))
(f) ))
You may want to skip the proof if you're mainly interested in how the decision agent works. Now we can give a proof of Proposition 3 that doesn't use Löb's theorem, and we can finally prove Conjecture 4 (now Proposition 4).
[1] Boolos, George. The Logic of Provability. Cambridge University Press: 1993. Ch. 17.
Continuing from here...
Is there a particular reason to define U as a constant? What if it was defined as a function, taking the agent function as its argument? For example:
U(#X) =
(a, 0) if X(#U,0) = C;
(b, 0) if X(#U,0) = D
Then A could be defined as:
A(#X, i) = y, such that there exists #z, such that z(#X, i)=y and forall #z' p_i(X(#z)) >= p_i(X(#z'))
[Some uniquness condition on y can be added for the cases where several actions may have equal maximal utility]
Then it should be provable that a>b => A(#U,0)=C and a A(#U,0)=D
This should also work with the toy PD. (But not with the real one - the agent's definition won't work because it is impossible to impersonate some other agent if you have to present your own Goedelian number).
There is no recursive function that takes the Gödel number of a function and computes the value of that function.
Huh? Of course, there is - the Universal Turing Machine. You were probably thinking of the halting problem, but here we can just assume every function halts.
[The agent idea was naive though. I was young and stupid when I wrote the grandfather comment :)]
Hmm. The agent is a recursive function, so it is equivalent to a Turing machine that halts, no?
But I see your point. There is no simple formula, so if nothing else, it's inelegant.
Whoops! I said in the OP that the precursor to A (before diagonalization) is a recursive function, but it's not. It's not computable because it has to check whether several propositions are theorems of Peano arithmetic, and also because of that existential quantifier in the definition of A. If A itself were recursive, then it would provably (in PA) cooperate or defect; but it cooperates or defects unprovably (in PA). I'll edit the OP to make it correct.
The rest of the post still works because all the functions are representable — they can be represented by formulas in arithmetic — even if they're not recursive. Thanks for bringing this to my attention.
EDIT: Oy, they're not even "representable" in the technical sense. They're only definable.
Continuing from here...
Is there a particular reason to define U as a constant? What if it was defined as a function, taking the agent function as its argument? For example:
U(#X) =
(a, 0) if X(#U, 0) = C;
(b, 0) if X(#U, 0) = D
Then A could be defined as:
A(#X, i) = y, such that there exists #z, such that z(#X, i)=y and forall #z' p_i(X(#z)) >= p_i(X(#z'))
[Some uniquness condition on y can be added for the cases where several actions may have equal maximal utility]
Then it should be provable that a>b => A(#U,0)=C and a A(#U,0)=D
This should also work with the toy PD. (But not with the real one - the agent's definition won't work because it is impossible to impersonate some other agent if you have to present your own Goedelian number).
I wrote this post in the course of working through Vladimir Slepnev's A model of UDT with a halting oracle. This post contains some of the ideas of Slepnev's post, with all the proofs written out. The main formal difference is that while Slepnev's post is about programs with access to a halting oracle, the "decision agents" in this post are formulas in Peano arithmetic. They are generally uncomputable and do not reason under uncertainty.
These ideas are due to Vladimir Slepnev and Vladimir Nesov. (Please let me know if I should credit anyone else.) I'm pretty sure none of this is original material on my part. It is possible that I have misinterpreted Slepnev's post or introduced errors.
We are going to define a world function) , a
, a 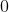 -ary function1 that outputs an ordered pair
-ary function1 that outputs an ordered pair  \in \mathbb{Q}^2) of payoff values. There are functions
of payoff values. There are functions 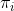 such that
such that  = a) and
and  = b) for any
for any 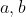 . In fact
. In fact ) is a function in the three variables
is a function in the three variables 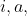 and
and 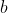 .
.
We are also going to define an agent function) that outputs the symbol
that outputs the symbol 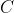 or
or 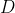 . The argument
. The argument 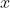 is supposed to be the Gödel number of the world function, and
is supposed to be the Gödel number of the world function, and 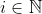 is some sort of indexical information.
is some sort of indexical information.
We want to define our agent such that
(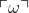 denotes the Gödel number of
denotes the Gödel number of 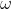 .
. 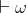 means that
means that 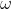 is provable in Peano arithmetic.
is provable in Peano arithmetic. 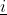 represents the numeral for
represents the numeral for 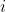 . I don't care what value
. I don't care what value ) has when
has when 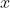 isn't the Gödel number of an appropriate
isn't the Gödel number of an appropriate 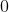 -ary function.)
-ary function.)
There is some circularity in this tentative definition, because a formula standing for appears in the definition of
appears in the definition of  itself. We get around this by using diagonalization. We'll describe how this works just this once: First define the function
itself. We get around this by using diagonalization. We'll describe how this works just this once: First define the function 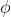 as follows:
as follows:
This function can be defined by a formula. Then the diagonal lemma gives us a formula such that
such that  = \phi(x,i,\ulcorner A \urcorner)) .
.
This is our (somewhat) rational decision agent. If it can prove it will do one thing, it does another; this is what Slepnev calls "playing chicken with the universe". If it can prove that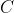 is an optimal strategy, it chooses
is an optimal strategy, it chooses 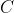 ; and otherwise it chooses
; and otherwise it chooses 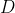 .
.
First, a lemma about the causes and consequences of playing chicken:
Lemma 1. For any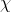 ,
,
(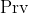 is a binary-valued function such that
is a binary-valued function such that ) is true exactly when there is a proof of
is true exactly when there is a proof of 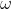 in Peano arithmetic. For brevity we write
in Peano arithmetic. For brevity we write ) instead.
instead. )) is the proposition that Peano arithmetic, plus the axiom that Peano arithmetic is consistent, is a consistent theory.)
is the proposition that Peano arithmetic, plus the axiom that Peano arithmetic is consistent, is a consistent theory.)
Proof. (1) By definition of ,
,
So
(2) By the principle of explosion,
(3) By the definition of ,
,
(4)
If we assume consistency of) (which entails consistency of
(which entails consistency of 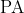 ), then parts (1) and (3) of Lemma 1 tell us that for any
), then parts (1) and (3) of Lemma 1 tell us that for any 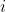 ,
,  = C) and
and  = D) . So the agent never actually plays chicken.
. So the agent never actually plays chicken.
Now let's see how our agent fares on a straightforward decision problem:
Proposition 2. Let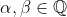 and suppose
and suppose
Assume consistency of) . Then
. Then  = C) if and only if
if and only if 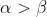 .
.
Proof. If we assume consistency of) , then Lemma 1 tells us that the agent doesn't play chicken. So the agent will choose
, then Lemma 1 tells us that the agent doesn't play chicken. So the agent will choose 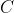 if and only if it determines that choosing
if and only if it determines that choosing 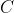 is optimal.
is optimal.
We have
Suppose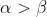 . Then clearly
. Then clearly
So = C) .
.
As for the converse: We have = C \to \pi_0 U() = \underline{\alpha})) . If also
. If also
and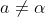 , then
, then  = D)) . By Lemma 1(3) and consistency of
. By Lemma 1(3) and consistency of ) , this cannot happen. So
, this cannot happen. So
Similarly, we have
for all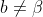 . So
. So
So the agent doesn't decide that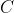 is optimal, and
is optimal, and  = D) .
.
Now let's see how fares on a symmetric Prisoner's Dilemma with itself:
fares on a symmetric Prisoner's Dilemma with itself:
Proposition 3. Let
Then, assuming consistency of) , we have
, we have  = C = A(\ulcorner U \urcorner,1)) .
.
Proof.
(This proof uses Löb's theorem, and that makes it confusing. Vladimir Slepnev points out that Löb's theorem is not really necessary here; a simpler proof appears in the comments.)
Looking at the definition of
By Lemma 1, (1) and (3),
Similarly,
So
Applying Lemma 1(2) and (4),
By Löb's theorem,
By) , we have
, we have
So, assuming)) , we conclude that
, we conclude that =C=A(\ulcorner U \urcorner,1)) .
.
The definition of treats the choices
treats the choices 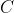 and
and 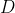 differently; so it is worth checking that
differently; so it is worth checking that  behaves correctly in the Prisoner's Dilemma when the effects of
behaves correctly in the Prisoner's Dilemma when the effects of 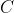 and
and 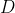 are switched:
are switched:
Proposition 4. Let
Then, assuming consistency of) , we have
, we have  = D = A(\ulcorner U \urcorner,1)) .
.
A proof appears in the comments.
There are a number of questions one can explore with this formalism: What is the correct generalization of that can choose between
that can choose between  actions, and not just two? How about infinitely many actions? What about theories other than Peano arithmetic? How do we accomodate payoffs that are real numbers? How do we make agents that can reason under uncertainty? How do we make agents that are computable algorithms rather than arithmetic formulas? How does
actions, and not just two? How about infinitely many actions? What about theories other than Peano arithmetic? How do we accomodate payoffs that are real numbers? How do we make agents that can reason under uncertainty? How do we make agents that are computable algorithms rather than arithmetic formulas? How does  fare on a Prisoner's Dilemma with asymmetric payoff matrix? In a two-person game where the payoff to player
fare on a Prisoner's Dilemma with asymmetric payoff matrix? In a two-person game where the payoff to player 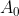 is independent of the behavior of
is independent of the behavior of 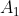 , can
, can 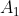 deduce the behavior of
deduce the behavior of 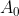 ? What happens when we replace the third line of the definition of
? What happens when we replace the third line of the definition of  with
with
? What is a (good) definition of "decision problem"? Is there a theorem that says that our agent is, in a certain sense, optimal?
is, in a certain sense, optimal?
1Every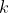 -ary function
-ary function 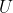 in this article is defined by a formula
in this article is defined by a formula ) with
with 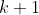 free variables such that
free variables such that ) and
and  \wedge \phi(x_1, \dots, x_k, y') \to y = y') . By a standard abuse of notation, when the name of a function like
. By a standard abuse of notation, when the name of a function like 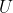 appears in a formula of arithmetic, what we really mean is the formula
appears in a formula of arithmetic, what we really mean is the formula 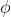 that defines it.
that defines it.