Ignoring the fact that some numbers need to be non-negative and sum up to 1, the basic mathematical issue here is some well-understood subtleties involving infinite-dimensional vector spaces. More specifically, let S be an infinite set. Then we can write down the following three (real) vector spaces from S:
Each of these spaces naturally sits inside of the next one. The VNM theorem should be regarded as describing certain linear functionals on the first vector space, which are uniquely determined by what they do to elements of S. Linear functionals on the second and third vector spaces are not uniquely determined by what they do to elements of S, the reason being that linear functionals only have to preserve finite linear combinations by default and this does not imply preserving infinite linear combinations. To preserve infinite linear combinations on the second vector space (a Lebesgue space ) we need some continuity hypothesis on the linear functional (Lebesgue spaces are in particular Banach spaces and have an induced topology ), which turns out to imply boundedness as a function on S essentially because of the St. Petersburg argument. The third vector space is even worse.
On the other hand, my impression is that the existence of pathological agents of the kind described in the OP (which in the language I'm using translates to pathological linear functionals on the second and third vector spaces) is independent of ZF but weaker than the axiom of choice. Similar objects such as Banach limits can be constructed using the Hahn-Banach theorem or the ultrafilter lemma. I've posted a math.stackexchange question about this.
I have serious doubts that any of these issues are relevant to agents in the real world.
That's a better explanation than mine. And thanks for asking what assumptions it takes for such agents to exist where people are more likely to know the answer; I should have thought of that.
I have serious doubts that any of these issues are relevant to agents in the real world.
Agreed.
I have serious doubts that any of these issues are relevant to agents in the real world.
I'm not sure about that. One relevant question is what happens if we restrict the set of priors our Bayesian utilitarians can have.
Why do we even need to deal with outcomes in the first place? For any outcome O, it is equivalent to the lottery L = pO where p = 1.
Also, how do you do LaTeX here?
You don't need to talk about outcomes, but I like to talk in terms of outcomes anyway because it makes it easier for me to interpret the lotteries. If you would rather not talk about outcomes, it shouldn't be too hard to mentally translate everything in the post in terms of lotteries.
Summary: The VNM utility theorem only applies to lotteries that involve a finite number of possible outcomes. If an agent maximizes the expected value of a utility function when considering lotteries that involve a potentially infinite number of outcomes as well, then its utility function must be bounded.
Outcomes versus Lotteries
One way to formulate the VNM utility theorem is in terms of outcomes and lotteries over outcomes. That is, there is some set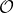 of outcomes, and a set
of outcomes, and a set 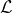 of lotteries defined as
of lotteries defined as 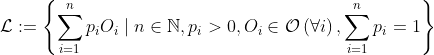 . In other words, the set of lotteries is the set of probability distributions over a finite number of outcomes. The finiteness is very important; we'll get to that later. Note that for each outcome, there is a corresponding lottery that guarantees this outcome, and these “pure outcome” lotteries are a basis for
. In other words, the set of lotteries is the set of probability distributions over a finite number of outcomes. The finiteness is very important; we'll get to that later. Note that for each outcome, there is a corresponding lottery that guarantees this outcome, and these “pure outcome” lotteries are a basis for 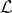 .
.
Given that formulation, and given the VNM axioms, there exists some function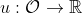 such that given any 2 lotteries
such that given any 2 lotteries 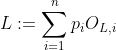 and
and 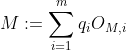 ,
, 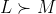 iff
iff 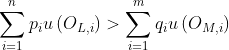 .
.
The other formulation does not mention . Instead, there is simply a set
. Instead, there is simply a set 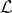 of lotteries, such that
of lotteries, such that 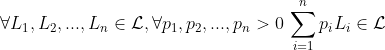 iff
iff 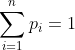 . In this formulation, there exists some function
. In this formulation, there exists some function 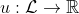 such that if
such that if  , then
, then 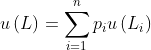 (notice
(notice  still must be finite) and for any 2 lotteries
still must be finite) and for any 2 lotteries 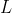 and
and 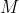 ,
, 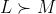 iff
iff 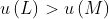 .
.
The formulation in terms of outcomes and lotteries over outcomes is more intuitively appealing (to me, at least), since real life has outcomes and uncertainty about outcomes, so I will use it when I can, but the formulation purely in terms of lotteries, which is more similar to what von Neumann and Morgenstern did in their original paper, will be useful sometimes, so I will switch back to it intermittently.
Infinite lotteries
Myth: Given some utility function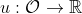 that accurately describes a VNM-rational agent's preferences over finite lotteries, if you expand
that accurately describes a VNM-rational agent's preferences over finite lotteries, if you expand 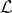 to include lotteries with an infinite number of possible outcomes (let's call the expanded set of lotteries
to include lotteries with an infinite number of possible outcomes (let's call the expanded set of lotteries  ), then for any 2 lotteries
), then for any 2 lotteries 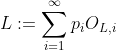 and
and 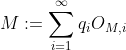 ,
, 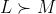 iff
iff 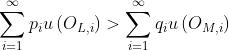 .
.
Reality: Knowing an agent's preferences over finite lotteries, and that the agent obeys the VNM axioms, does not tell you everything about the agent's preferences over lotteries with an infinite number of possible outcomes. To demonstrate this, I'm going to construct a VNM-rational agent that maximizes a utility function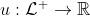 , where
, where  . This construction relies on the axiom of choice (please let me know if you figure out whether or not it is possible to construct such an agent without the axiom of choice). I will also be assuming that
. This construction relies on the axiom of choice (please let me know if you figure out whether or not it is possible to construct such an agent without the axiom of choice). I will also be assuming that 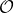 is countably infinite (if
is countably infinite (if  is finite, such an agent is impossible, and if it is uncountable, then you can consider a countable subset).
is finite, such an agent is impossible, and if it is uncountable, then you can consider a countable subset).
Notice that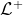 can be seen as a subset of the real vector space
can be seen as a subset of the real vector space 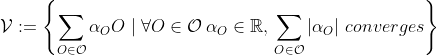 , with the addition and multiplication by scalar operations being exactly what you would expect (
, with the addition and multiplication by scalar operations being exactly what you would expect (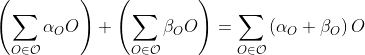 , and
, and 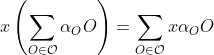 ). A utility function
). A utility function 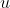 can be seen as an element of the dual space of
can be seen as an element of the dual space of 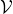 . The axiom of choice implies that this vector space has a basis (in this context, a basis means a set of vectors for which any finite subset is linearly independent, and every vector is a linear combination of a finite number of basis vectors). The value of
. The axiom of choice implies that this vector space has a basis (in this context, a basis means a set of vectors for which any finite subset is linearly independent, and every vector is a linear combination of a finite number of basis vectors). The value of 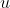 on each basis element can be chosen independently, and these choices completely determine
on each basis element can be chosen independently, and these choices completely determine 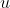 . In particular, the basis could contain every element of
. In particular, the basis could contain every element of 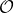 , and also contain
, and also contain 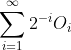 for some sequence
for some sequence 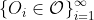 with distinct elements. Then we could have
with distinct elements. Then we could have 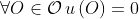 and
and  , violating the conclusion of the myth, but this meets all the VNM axioms.
, violating the conclusion of the myth, but this meets all the VNM axioms.
The fact that there is a real-valued function on lotteries that the agent maximizes guarantees that the completeness and transitivity axioms hold, since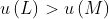 or
or 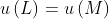 or
or 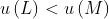 (completeness), and if
(completeness), and if 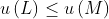 and
and 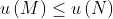 then
then 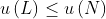 (transitivity). The fact that the function is linear with respect to finite sums guarantees that the continuity and independence axioms hold, since if
(transitivity). The fact that the function is linear with respect to finite sums guarantees that the continuity and independence axioms hold, since if 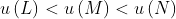 then
then 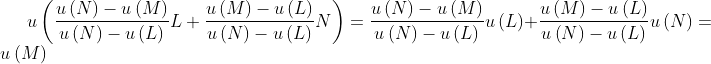 (continuity), and if
(continuity), and if 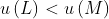 then for any lottery
then for any lottery 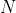 and positive probability
and positive probability 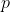 ,
, 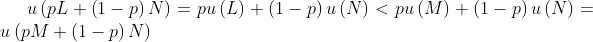 (independence).
(independence).
Extended VNM hypothesis
The VNM utility theorem does not prove that an agent meeting its axioms will maximize the expected value of a utility function when presented with infinite lotteries, but the fact that any such agent will maximize the expected value of a utility function when presented with finite lotteries certainly seems very suggestive. With that in mind, I suggest that this be called the “extended von Neumann-Morgenstern hypothesis”:
An agent, in order to be considered rational, should maximize the expected value of a utility function over outcomes when choosing between lotteries over any (possibly infinite) number of outcomes.
Bounded and unbounded utility functions
It is perfectly possible to construct VNM-rational agents with an unbounded utility function. But all such agents will inevitably violate the extended VNM hypothesis, because it is possible to create infinite lotteries with undefined expected value. For instance, the St. Petersburg paradox can be modified to refer specifically to utilities instead of money. That is, if there is no upper bound to the agent's utility function, then there exists a sequence of outcomes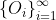 such that for each
such that for each 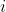 ,
, 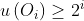 . Then the expected utility of
. Then the expected utility of 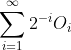 is
is 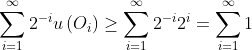 , which does not converge. So unbounded utility functions are not compatible with the extended VNM hypothesis.
, which does not converge. So unbounded utility functions are not compatible with the extended VNM hypothesis.
At this point, one may feel a strong temptation to come up with some way to characterize the values of infinite sums with some ordered superset of the real numbers, so that it is possible to compare nonconvergent sums. However, by the formulation of the VNM theorem solely in terms of lotteries, the utility of any lottery, such as , is a real number. So any such scheme that requires that the range of the utility function include nonreals will violate the VNM axioms. In particular, it will probably violate the archimedian axiom.
, is a real number. So any such scheme that requires that the range of the utility function include nonreals will violate the VNM axioms. In particular, it will probably violate the archimedian axiom.
One possible response to this is to dismiss the archimedian axiom, and try to characterize agents that obey the completeness, transitivity, and independence axioms. Benja has written (section "Doing without Continuity) about this, and I find his solution fairly compelling, but it isn't clear that it helps us deal with situations like the St. Petersburg paradox. I intend to say more about nonarchimedian preferences soon.