Incidentally, at the MIRI workshop, we soon started referring to the source-code-swap Prisoner's Dilemma between two modal agents as "modal combat".
Or "MODAL COMBAT!", if you prefer.
One downside of having a bot that's too complicated is that it makes the other bot less likely to trust you.
An interesting question is to what extent a similar phenomenon is present in human relationships.
When people make purchasing decisions, pricing models that are too complex make them less likely to purchase. If it's too confusing to figure out whether something is a good deal or not, we generally tend to just assume it's a bad deal. See http://ideas.repec.org/p/ags/ualbsp/24093.html (Choice Environment, Market Complexity and Consumer Behavior: A Theoretical and Empirical Approach for Incorporating Decision Complexity into Models of Consumer Choice), for example.
Wow, MIRI is just churning out [1] math papers now.
[1]: Using this expression entirely in a positive sense.
Actually, "MIRI is just churning out writeups of research which happened over a long preceding time", which I'd emphasize because I think there's some sort of systematic "science as press release bias" wherein people think about science as though it occurs in bursts of press releases because that's what they externally observe. Not aimed at you in particular but seems like an important general observation. We couldn't do twice as much research by writing twice as many papers.
Patrick, congrats on writing this up! It's nice to see MIRI step up its game.
Will two PrudentBots cooperate if they're using theories of different strength?
I don't have any background in automated proofs; could someone please outline the practical implications of this, considering the algorithmic complexity involved?
How effective would a real PrudentBot be if written today? What amount of complexity in opponent programs could it handle? How good are proof-searching algorithms? How good are computer-assisted humans searching for proofs about source code they are given?
Are there formal languages designed so that if an agent is written in them, following certain rules with the intent to make its behavior obvious, it is significantly easier (or more probable) for a proof-finding algorithm to analyze its behavior? Without, of course, restricting the range of behaviors that can be expressed in that design.
Stupid question: are there clear examples of any real-life events that would actually correspond to classic, one-shot Prisoner's Dilemma? I thought that I knew of plenty of examples before, but when I was challenged to name some, all the ones I could think of failed some of the conditions, like being tragedies of the commons rather than PD, or being iterated PD rather than one-shot PD, or the players being able to adapt their plans based on the way the opponent reacts instead of it being a single all-or-nothing choice (arms races are sometimes held up as an example of PD, but there both sides have access to intelligence reports on the kind of strategy that the enemy seems to be adopting, and can adjust their strategy accordingly).
Of course, one can always construct hypothetical scenarios in a way that makes them classic one-shot PD by construction, but being unable to name any clear real-life examples would seem to suggest that this particular scenario isn't that interesting to focus on.
The point of using the one-shot Prisoner's Dilemma (and variants like this one) isn't actually that it's a realistic approximation of real-life phenomena, so much as that it's one of the simplest decision-theory problems that standard game theory looks suboptimal for, and so it's a good proving ground for further development. (Think of it like the assumption that objects in kinetic physics are frictionless.)
Similarly, game theory started with assumptions of perfect common knowledge of payoff matrices, which didn't model real-life situations all that well, but the theory developed there was later extended to more realistic setups in politics and business.
That being said, I'm also curious to know if there are real-world examples that model one-shot Prisoner's Dilemmas reasonably well.
I found situation where PrudentBot behaves suboptimally and a more intelligent agent can do better. I'm considering an opponent I call pseudo tit-for-tat at level N, or PsTitTatBot[N]. PsTitTatBot[0] is simply CooperateBot. For N>0, the strategy for PsTitTatBot[N] is to simulate its opponent running against PsTitTatBot[N-1], and do the same thing its opponent did in the simulation. PrudentBot would have an outcome of (D,D) against PsTitTatBot[N] for any N. However, it's easy for an agent to ensure that against sufficiently high level tit-for-tat agent the outcome will be (C,C). To do this, there must be a specific N such that this agent plays suboptimally against PsTitTatBot[N]. However, the benefit of mutual cooperation at higher levels should compensate for that.
Sounds awesome, great job !
But there is something I didn't get : what does Con() mean in PA+Con(PA) ? Maybe it's stupid question and everyone is supposed to know, but I don't remember ever encountering that symbol, and I can't find it's meaning, neither on Wikipedia nor on mathworld...
It means consistent. PA + Con(PA) means PA together with the axiom that PA is consistent (which can be expressed in PA because PA can express "PA proves X," so "PA is consistent" can be expressed as "PA does not prove a contradiction").
Suppose we decide that proving systems are too (NP) hard and we want to restrict agents to polynomial time. If an agent has access to a random coin, can it interactively prove that its opponent is cooperative?
I stumbled across an interesting class of agent while attempting to design a probabilistically proving bot for AlexMennen's contest. The agent below always cooperates with opponents who always cooperate back, (almost) always defects against opponents who always defect against them, and runs in probabilistic polynomial time if its opponent does as we...
Stupid question... Can one construct ImpudentBot, specifically designed to defeat the analysis done by PrudentBot, say, by forcing it to never halt or something? Or PrudeBot, which resists all attempts at uncovering its true appearance?
PrudentBot halts on all inputs. More accurately, I should say, the modal form of PrudentBot has an output that's always decidable in PA+2, while the algorithm version only looks for proofs up to a certain pre-specified length, and thus always halts. In either case, PrudentBot defects by default if it cannot prove anything.
So ImpudentBot is not possible, and PrudeBot earns a big fat D from PrudentBot.
Incidentally, this is the big distinction between "programs that try and run other programs' code" and "programs that try to prove things about other programs' output": Löb's Theorem allows you to avoid the danger of infinite regress.
You can't get more points than PrudentBot in one-to-one combat, but you can try doing better against the environment (other players).
There is always an environment where agent X gets more points than PrudentBot. Specifically, an environment of ServantOfX bots that recognize the source code of X, cooperate with X, and defect against everyone else.
Technically, there is a difference between "maximizing your score" and "beating PrudentBot". (Focusing on "beating PrudentBot" makes it a zero-sum game.) If you know in advance that there will be more copies of you than copies of PrudentBot, you could just decide to defect against PrudentBot, which will harm it more than it will harm you. But it will harm you. You will defeat PrudentBot, but get less utility than you could get otherwise. (You will prove suboptimality of PrudentBot by becoming suboptimal yourself.)
I'm coming to this quite late, and these are the notes I wrote as I read the paper, before reading the comments, followed by my notes in the comments.
Has any of the (roughest) analysis been done to bound proving time for PrudentBot? It should be fairly trivial to get very bad bounds and if those are not so bad that seems like a worthwhile thing to know (although what does "not so bad" really mean I guess is a problem.)
Is there a good (easy) reference for the statement about quining in PA (on page 6 below CliqueBot)? Under modal agents Kleene's r...
Haskell code to run PrudentBot (quickly) and the other bots (also quickly) can be found on github here:
The nice part about modal agents is that there are simple tools for finding the fixed points without having to search through proofs; in fact, Mihaly and Marcello wrote up a computer program to deduce the outcome of the source-code-swap Prisoner's Dilemma between any two (reasonably simple) modal agents. These tools also made it much easier to prove general theorems about such agents.
Would it be possible to make this program publicly available? I'm curious about how certain modal agents play against each other, but struggling to caculate it manually.
It seems to me that TrollBot is sufficiently self-destructive that you are unlikely to encounter it in practice.
I wonder if there are heuristics you can use that would help you not worry too much about those cases.
Actually, since this is a deterministic setup, you can go one better and consider an 'iterated tournament' as a difference equation in N-dimensional space, where N is the number of strategies you include, and the dimensions represent the proportion of the total population; then you can demonstrate the trajectories the demographics will take from any starting location. There will be a handful of point equilibria, as well as several equilibrium lines (actually, I think, an equilibrium volume, but this depends on which strategies you include), and you can talk about which equilbria are stable / unstable, and decide not to care about strategies who only exist in unstable equilibria. You probably need to require that the population space is seeded with CooperateBot, DefectBot, and possibly FairBot, in order to get neat results.
Here is another obstacle to an optimality result: define UnfairBot as the agent which cooperate with X if and only if PA prove that X defect against UnfairBot, then no modal agent can get both FairBot and UnfairBot to cooperate with it.
I have two proposed alternatives to PrudentBot.
If you can prove a contradiction, defect. Otherwise, if you can prove that your choice will be the same as the opponent's, cooperate. Otherwise, defect.
If you can prove that, if you cooperate, the other agent will cooperate, and you can't prove that if you defect, the other agent will cooperate, then cooperate. Otherwise, defect.
Both of these are unexploitable, cooperate with themselves, and defect against CooperateBot, if my calculations are correct. The first one is a simple way of "sanitizing&q...
Thanks for posting this! I'm glad to see more work explained well and formally, and hope to continue seeing preprints like this here.
I'm much happier with this approach than I was a year ago. I don't know how much of that is change on its part, and how much is change on my part; probably some of both.
This echoes the impossibility-of-optimality results of Anderlini [2] and Canning [6] on game theory for Turning machines with access to each others' source codes.
Turning -> Turing
FairBot references itself in its de finition, but as with CliqueBot , this can be done via Kleene's recursion theorem
Should there be a reference to Kleene's recursion theorem, or is this common background knowledge for your target audience?
It turns out that, even within the class of modal agents, it's hard to formulate a definition of optimality that's actually true of something, and which meaningfully corresponds to our intuitions about the "right" decisions on decision-theoretic problems. (This intuition is not formally defined, so I'm using scare quotes.)
This seems too simple, but why can't PrudentBot search for a proof that (X(PrudentBot) = C and PrudentBot(X) = D) and defect if a proof is found. If no proof is found, search for the proof of (X(PrudentBot) = C) as before.
I propose a variation of fairbot, let's call it two-tiered fairbot (TTF).
If the opponent cooperates iff I cooperate, cooperate
else, if the opponent cooperates iff (I cooperate iff the opponent cooperates), check to see if the opponent cooperates
and cooperate iff he/she does*
else, defect.
It seems to cooperate against any "reasonable" agents, as well as itself (unless there's something I'm missing) while defecting against cooperatebot. Any thoughts?
*As determined by proof check.
How is "Given an opponent that defects against Defectbot, PrudentBot's behavior is to cooperate with that program IFF PrudentBot can prove that it cooperates with that program" proven? (That is the case stated where PrudentBot plays against itself)
Has it been shown in general that there exists a proof in PA that all agent Y cooperates with PrudentBot for complicated agents Y?
Didn't know about the problems setting. So cool!
Some random thought, sorry if none is relevant:
I think my next step towards optimality would have been not to look for an optimal agent but for an optimal act of choosing the agent - as action optimality is better understood than agent optimality. Than I would look at stable mixed equilibria to see if any of them is computable. If any is, I'll be interested at the agent that implement it (ie randomise another agent and then simulate it)
BTW now that I think about it I see that allowing the agent to randomise i...
I finally had time to read this, and I must say, that's an extremely creative premise. I'm puzzled by the proof of theorem 3.1, however. It claims "By inspection of FairBot, PA⊢◻(FB(FB) = C)-->FB(FB=C)."
However, by inspection of fairbot, the antecedent of the conditional should be FB(FB) = C rather than ◻(FB(FB) = C). The code says "if it's a theorem of PA that X cooperates with me, then cooperate." It doesn't say "if it's a theorem of PA that it's provable in PA that X cooperates with me, then cooperate." So I don't believe you can appeal to Lob's theorem in this case. .
I am bothered by the fact that the reasoning that leads to PrudentBot seems to contradict the reasoning of decision theory. Specifially, the most basic and obvious fact of behavior in these competitive games is: if you can prove that the opponent cooperates if and only if you do, then you should cooperate. But this reasoning gives the wrong answer vs. CooperateBot, for Lobian reasons. Is there an explanation for this gap?
What about the agent represented by the formula "P iff provable(P iff Q)"? It clearly cooperates with itself, and its bounded version should be able to do so with much less computing power than PrudentBot would need. What does it do against PrudentBot and FairBot? Is there anything wrong with it?
Two questions about the paper:
Would it be possible to specify FairBot directly as a formula (rather than a program, which is now the case)?
Also, I'm somewhat confused about the usage of FB(FB)=C, as FB(FB) should be a formula/sentence and not a term. Is it correct to read "FB(FB)=C" as "\box FB(FB)" and "FB(FB)=D" as "\box ~FB(FB)"? Or should it be without boxes?
Why do you associate a rank with each modal agent? It looks like it's designed to prevent situations where there are 2 modal agents X and Y such that X tests its opponent against Y and Y tests its opponent against X, but why do such situations need to be avoided? Doesn't the diagonal lemma make them possible?
I'm not convinced that FairBot cooperates with itself. If we call the statement that FairBot self-cooperates S, then it is not the case that we know that (There exists a proof of S) -> S [which would imply S by Lob's Theorem]. Instead, what we know is (There exists a proof of S of length at most Ackermann(20)) -> S. I'm not convinced that this is enough to conclude S. In fact, I am somewhat doubtful that S is true.
In particular, I can also prove (There exists a proof of (not S) of length at most Ackermann(20)) -> (not S). This is by case analysis:...
Suppose we decide that proving systems are too (NP) hard and we want to restrict agents to polynomial time. If an agent has access to a random coin, can it interactively prove that its opponent is cooperative?
I stumbled across an interesting class of agent while attempting to design a probabilistically proving bot for AlexMennen's contest. The agent below always cooperates with opponents who always cooperate back, (almost) always defects against opponents who always defect against them, and runs in probabilistic polynomial time if its opponent does as well.
def mimic_bot(opponent):
if random() > ε:
my_source = quine_my_source()
return eval(opponent, my_source) # do as your opponent does to you
else:
# unlikely, but necessary to break out of recursive simulations in polynomial time
return COOPERATE
This particular agent is a bit naïve, but more sophisticated versions (e.g ones that do not cooperate with CooperateBot) are possible. Does anyone have any insight on probabilistically proving opponents will cooperate?
I'm proud to announce the preprint of Robust Cooperation in the Prisoner's Dilemma: Program Equilibrium via Provability Logic, a joint paper with Mihaly Barasz, Paul Christiano, Benja Fallenstein, Marcello Herreshoff, Patrick LaVictoire (me), and Eliezer Yudkowsky.
This paper was one of three projects to come out of the 2nd MIRI Workshop on Probability and Reflection in April 2013, and had its genesis in ideas about formalizations of decision theory that have appeared on LessWrong. (At the end of this post, I'll include links for further reading.)
Below, I'll briefly outline the problem we considered, the results we proved, and the (many) open questions that remain. Thanks in advance for your thoughts and suggestions!
Background: Writing programs to play the PD with source code swap
(If you're not familiar with the Prisoner's Dilemma, see here.)
The paper concerns the following setup, which has come up in academic research on game theory: say that you have the chance to write a computer program X, which takes in one input and returns either Cooperate or Defect. This program will face off against some other computer program Y, but with a twist: X will receive the source code of Y as input, and Y will receive the source code of X as input. And you will be given your program's winnings, so you should think carefully about what sort of program you'd write!
Of course, you could simply write a program that defects regardless of its input; we call this program DefectBot, and call the program that cooperates on all inputs CooperateBot. But with the wealth of information afforded by the setup, you might wonder if there's some program that might be able to achieve mutual cooperation in situations where DefectBot achieves mutual defection, without thereby risking a sucker's payoff. (Douglas Hofstadter would call this a perfect opportunity for superrationality...)
Previously known: CliqueBot and FairBot
And indeed, there's a way to do this that's been known since at least the 1980s. You can write a computer program that knows its own source code, compares it to the input, and returns C if and only if the two are identical (and D otherwise). Thus it achieves mutual cooperation in one important case where it intuitively ought to: when playing against itself! We call this program CliqueBot, since it cooperates only with the "clique" of agents identical to itself.
There's one particularly irksome issue with CliqueBot, and that's the fragility of its cooperation. If two people write functionally analogous but syntactically different versions of it, those programs will defect against one another! This problem can be patched somewhat, but not fully fixed. Moreover, mutual cooperation might be the best strategy against some agents that are not even functionally identical, and extending this approach requires you to explicitly delineate the list of programs that you're willing to cooperate with. Is there a more flexible and robust kind of program you could write instead?
As it turns out, there is: in a 2010 post on LessWrong, cousin_it introduced an algorithm that we now call FairBot. Given the source code of Y, FairBot searches for a proof (of less than some large fixed length) that Y returns C when given the source code of FairBot, and then returns C if and only if it discovers such a proof (otherwise it returns D). Clearly, if our proof system is consistent, FairBot only cooperates when that cooperation will be mutual. But the really fascinating thing is what happens when you play two versions of FairBot against each other. Intuitively, it seems that either mutual cooperation or mutual defection would be stable outcomes, but it turns out that if their limits on proof lengths are sufficiently high, they will achieve mutual cooperation!
The proof that they mutually cooperate follows from a bounded version of Löb's Theorem from mathematical logic. (If you're not familiar with this result, you might enjoy Eliezer's Cartoon Guide to Löb's Theorem, which is a correct formal proof written in much more intuitive notation.) Essentially, the asymmetry comes from the fact that both programs are searching for the same outcome, so that a short proof that one of them cooperates leads to a short proof that the other cooperates, and vice versa. (The opposite is not true, because the formal system can't know it won't find a contradiction. This is a subtle but essential feature of mathematical logic!)
Generalization: Modal Agents
Unfortunately, FairBot isn't what I'd consider an ideal program to write: it happily cooperates with CooperateBot, when it could do better by defecting. This is problematic because in real life, the world isn't separated into agents and non-agents, and any natural phenomenon that doesn't predict your actions can be thought of as a CooperateBot (or a DefectBot). You don't want your agent to be making concessions to rocks that happened not to fall on them. (There's an important caveat: some things have utility functions that you care about, but don't have sufficient ability to predicate their actions on yours. In that case, though, it wouldn't be a true Prisoner's Dilemma if your values actually prefer the outcome (C,C) to (D,C).)
However, FairBot belongs to a promising class of algorithms: those that decide on their action by looking for short proofs of logical statements that concern their opponent's actions. In fact, there's a really convenient mathematical structure that's analogous to the class of such algorithms: the modal logic of provability (known as GL, for Gödel-Löb).
So that's the subject of this preprint: what can we achieve in decision theory by considering agents defined by formulas of provability logic?
More formally (skip the next two paragraphs if you're willing to trust me), we inductively define the class of "modal agents" as formulas using propositional variables and logical connectives and the modal operator (which represents provability in some base-level formal system like Peano Arithmetic), of the form
(which represents provability in some base-level formal system like Peano Arithmetic), of the form ) , where
, where 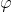 is fully modalized (i.e. all instances of variables are contained in an expression
is fully modalized (i.e. all instances of variables are contained in an expression 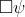 ), and with each
), and with each 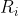 corresponding to a fixed modal agent of lower rank. For example, FairBot is represented by the modal formula
corresponding to a fixed modal agent of lower rank. For example, FairBot is represented by the modal formula 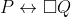 .
.
When two modal agents play against each other, the outcome is given by the unique fixed point of the system of modal statements, where the variables are identified with each other so that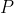 represents the expression
represents the expression =C) ,
, 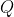 represents
represents =C) , and the
, and the 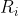 represent the actions of lower-rank modal agents against
represent the actions of lower-rank modal agents against 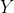 and vice-versa. (Modal rank is defined as a natural number, so this always bottoms out in a finite number of modal statements; also, we interpret outcomes as statements of provability in Peano Arithmetic, evaluated in the model where PA is consistent, PA+Con(PA) is consistent, and so on. See the paper for the actual details.)
and vice-versa. (Modal rank is defined as a natural number, so this always bottoms out in a finite number of modal statements; also, we interpret outcomes as statements of provability in Peano Arithmetic, evaluated in the model where PA is consistent, PA+Con(PA) is consistent, and so on. See the paper for the actual details.)
The nice part about modal agents is that there are simple tools for finding the fixed points without having to search through proofs; in fact, Mihaly and Marcello wrote up a computer program to deduce the outcome of the source-code-swap Prisoner's Dilemma between any two (reasonably simple) modal agents. These tools also made it much easier to prove general theorems about such agents.
PrudentBot: The best of both worlds?
Can we find a modal agent that seems to improve on FairBot? In particular, we should want at least the following properties:
It's nontrivial that such an agent exists: you may remember the post I wrote about the Masquerade agent, which is a modal agent that does almost all of those things (it doesn't cooperate with the original FairBot, though it does cooperate with some more complicated variants), and indeed we didn't find anything better until after we had Mihaly and Marcello's modal-agent-evaluator to help us.
But as it turns out, there is such an agent, and it's pretty elegant: we call it PrudentBot, and its modal version cooperates with another agent Y if and only if (there's a proof in Peano Arithmetic that Y cooperates with PrudentBot and there's a proof in PA+Con(PA) that Y defects against DefectBot). This agent can be seen to satisfy all of our criteria. But is it optimal among modal agents, by any reasonable criterion?
Results: Obstacles to Optimality
It turns out that, even within the class of modal agents, it's hard to formulate a definition of optimality that's actually true of something, and which meaningfully corresponds to our intuitions about the "right" decisions on decision-theoretic problems. (This intuition is not formally defined, so I'm using scare quotes.)
There are agents that give preferential treatment to DefectBot, FairBot, or even CooperateBot, compared to PrudentBot, though these agents are not ones you'd program in an attempt to win at the Prisoner's Dilemma. (For instance, one agent that rewards CooperateBot over PrudentBot is the agent that cooperates with Y iff PA proves that Y cooperates against DefectBot; we've taken to jokingly calling that agent TrollBot.) One might well suppose that a modal agent could still be optimal in the sense of making the "right" decision in every case, regardless of whether it's being punished for some other decision. However, this is not the only obstacle to a useful concept of optimality.
The second obstacle is that any modal agent only checks proofs at some finite number of levels on the hierarchy of formal systems, and agents that appear indistinguishable at all those levels may have obviously different "right" decisions. And thirdly, an agent might mimic another agent in such a way that the "right" decision is to treat the mimic differently from the agent it imitates, but in some cases one can prove that no modal agent can treat the two differently.
These three strikes appear to indicate that if we're looking to formalize more advanced decision theories, modal agents are too restrictive of a class to work with. We might instead allow things like quantifiers over agents, which would invalidate these specific obstacles, but may well introduce new ones (and certainly would make for more complicated proofs). But for a "good enough" algorithm on the original problem (assuming that the computer will have lots of computational resources), one could definitely do worse than submit a finite version of PrudentBot.
Why is this awesome, and what's next?
In my opinion, the result of Löbian cooperation deserves to be published for its illustration of Hofstadterian superrationality in action, apart from anything else! It's really cool that two agents reasoning about each other can in theory come to mutual cooperation for genuine reasons that don't have to involve being clones of each other (or other anthropic dodges). It's a far cry from a practical approach, of course, but it's a start: mathematicians always begin with a simplified and artificial model to see what happens, then add complications one at a time.
As for what's next: First, we don't actually know that there's no meaningful non-vacuous concept of optimality for modal agents; it would be nice to know that one way or another. Secondly, we'd like to see if some other class of agents contains a simple example with really nice properties (the way that classical game theory doesn't always have a pure Nash equilibrium, but always has a mixed one). Thirdly, we might hope that there's an actual implementation of a decision theory (TDT, UDT, etc) in the context of program equilibrium.
If we succeed in the positive direction on any of those, we'd next want to extend them in several important ways: using probabilistic information rather than certainty, considering more general games than the Prisoner's Dilemma (bargaining games have many further challenges, and games of more than two players could be more convoluted still), etc. I personally hope to work on such topics in future MIRI workshops.
Further Reading on LessWrong
Here are some LessWrong posts that have tackled similar material to the preprint: