Preamble
Double crux is one of CFAR's newer concepts, and one that's forced a re-examination and refactoring of a lot of our curriculum (in the same way that the introduction of TAPs and Inner Simulator did previously). It rapidly became a part of our organizational social fabric, and is one of our highest-EV threads for outreach and dissemination, so it's long overdue for a public, formal explanation.
Note that while the core concept is fairly settled, the execution remains somewhat in flux, with notable experimentation coming from Julia Galef, Kenzi Amodei, Andrew Critch, Eli Tyre, Anna Salamon, myself, and others. Because of that, this post will be less of a cake and more of a folk recipe—this is long and meandering on purpose, because the priority is to transmit the generators of the thing over the thing itself. Accordingly, if you think you see stuff that's wrong or missing, you're probably onto something, and we'd appreciate having them added here as commentary.
Casus belli
To a first approximation, a human can be thought of as a black box that takes in data from its environment, and outputs beliefs and behaviors (that black box isn't really "opaque" given that we do have access to a lot of what's going on inside of it, but our understanding of our own cognition seems uncontroversially incomplete).
When two humans disagree—when their black boxes output different answers, as below—there are often a handful of unproductive things that can occur.
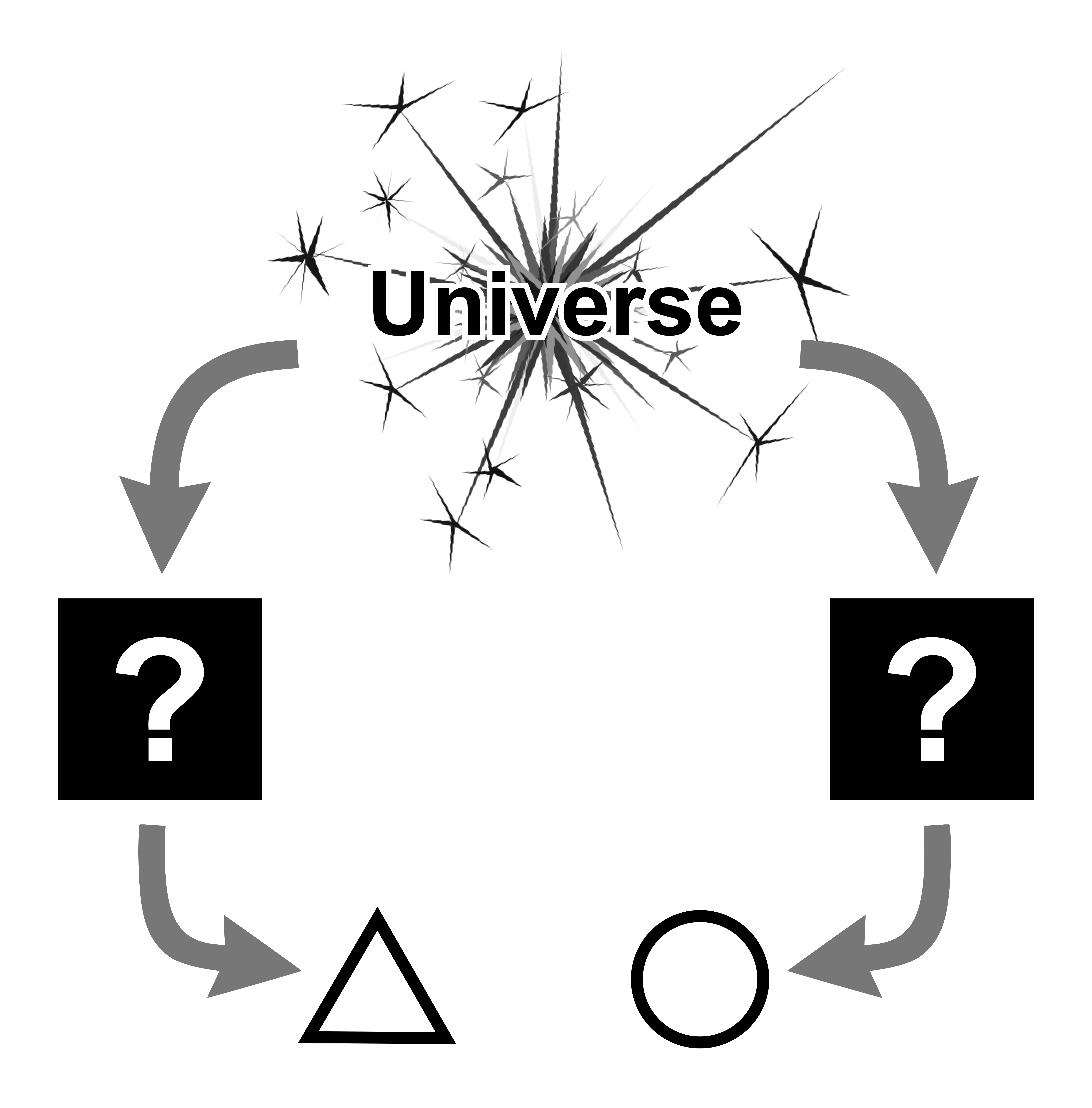
The most obvious (and tiresome) is that they'll simply repeatedly bash those outputs together without making any progress (think most disagreements over sports or politics; the people above just shouting "triangle!" and "circle!" louder and louder). On the second level, people can (and often do) take the difference in output as evidence that the other person's black box is broken (i.e. they're bad, dumb, crazy) or that the other person doesn't see the universe clearly (i.e. they're biased, oblivious, unobservant). On the third level, people will often agree to disagree, a move which preserves the social fabric at the cost of truth-seeking and actual progress.
Double crux in the ideal solves all of these problems, and in practice even fumbling and inexpert steps toward that ideal seem to produce a lot of marginal value, both in increasing understanding and in decreasing conflict-due-to-disagreement.
Prerequisites
This post will occasionally delineate two versions of double crux: a strong version, in which both parties have a shared understanding of double crux and have explicitly agreed to work within that framework, and a weak version, in which only one party has access to the concept, and is attempting to improve the conversational dynamic unilaterally.
In either case, the following things seem to be required:
- Epistemic humility. The number one foundational backbone of rationality seems, to me, to be how readily one is able to think "It's possible that I might be the one who's wrong, here." Viewed another way, this is the ability to take one's beliefs as object, rather than being subject to them and unable to set them aside (and then try on some other belief and productively imagine "what would the world be like if this were true, instead of that?").
- Good faith. An assumption that people believe things for causal reasons; a recognition that having been exposed to the same set of stimuli would have caused one to hold approximately the same beliefs; a default stance of holding-with-skepticism what seems to be evidence that the other party is bad or wants the world to be bad (because as monkeys it's not hard for us to convince ourselves that we have such evidence when we really don't).1
- Confidence in the existence of objective truth. I was tempted to call this "objectivity," "empiricism," or "the Mulder principle," but in the end none of those quite fit. In essence: a conviction that for almost any well-defined question, there really truly is a clear-cut answer. That answer may be impractically or even impossibly difficult to find, such that we can't actually go looking for it and have to fall back on heuristics (e.g. how many grasshoppers are alive on Earth at this exact moment, is the color orange superior to the color green, why isn't there an audio book of Fight Club narrated by Edward Norton), but it nevertheless exists.
- Curiosity and/or a desire to uncover truth. Originally, I had this listed as truth-seeking alone, but my colleagues pointed out that one can move in the right direction simply by being curious about the other person and the contents of their map, without focusing directly on the territory.
At CFAR workshops, we hit on the first and second through specific lectures, the third through osmosis, and the fourth through osmosis and a lot of relational dynamics work that gets people curious and comfortable with one another. Other qualities (such as the ability to regulate and transcend one's emotions in the heat of the moment, or the ability to commit to a thought experiment and really wrestle with it) are also helpful, but not as critical as the above.
How to play
Let's say you have a belief, which we can label A (for instance, "middle school students should wear uniforms"), and that you're in disagreement with someone who believes some form of ¬A. Double cruxing with that person means that you're both in search of a second statement B, with the following properties:
- You and your partner both disagree about B as well (you think B, your partner thinks ¬B).
- The belief B is crucial for your belief in A; it is one of the cruxes of the argument. If it turned out that B was not true, that would be sufficient to make you think A was false, too.
- The belief ¬B is crucial for your partner's belief in ¬A, in a similar fashion.

In the example about school uniforms, B might be a statement like "uniforms help smooth out unhelpful class distinctions by making it harder for rich and poor students to judge one another through clothing," which your partner might sum up as "optimistic bullshit." Ideally, B is a statement that is somewhat closer to reality than A—it's more concrete, grounded, well-defined, discoverable, etc. It's less about principles and summed-up, induced conclusions, and more of a glimpse into the structure that led to those conclusions.
(It doesn't have to be concrete and discoverable, though—often after finding B it's productive to start over in search of a C, and then a D, and then an E, and so forth, until you end up with something you can research or run an experiment on).
At first glance, it might not be clear why simply finding B counts as victory—shouldn't you settle B, so that you can conclusively choose between A and ¬A? But it's important to recognize that arriving at B means you've already dissolved a significant chunk of your disagreement, in that you and your partner now share a belief about the causal nature of the universe.
If B, then A. Furthermore, if ¬B, then ¬A. You've both agreed that the states of B are crucial for the states of A, and in this way your continuing "agreement to disagree" isn't just "well, you take your truth and I'll take mine," but rather "okay, well, let's see what the evidence shows." Progress! And (more importantly) collaboration!
Methods
This is where CFAR's versions of the double crux unit are currently weakest—there's some form of magic in the search for cruxes that we haven't quite locked down. In general, the method is "search through your cruxes for ones that your partner is likely to disagree with, and then compare lists." For some people and some topics, clearly identifying your own cruxes is easy; for others, it very quickly starts to feel like one's position is fundamental/objective/un-break-downable.
Tips:
- Increase noticing of subtle tastes, judgments, and "karma scores." Often, people suppress a lot of their opinions and judgments due to social mores and so forth. Generally loosening up one's inner censors can make it easier to notice why we think X, Y, or Z.
- Look forward rather than backward. In places where the question "why?" fails to produce meaningful answers, it's often more productive to try making predictions about the future. For example, I might not know why I think school uniforms are a good idea, but if I turn on my narrative engine and start describing the better world I think will result, I can often sort of feel my way toward the underlying causal models.
- Narrow the scope. A specific test case of "Steve should've said hello to us when he got off the elevator yesterday" is easier to wrestle with than "Steve should be more sociable." Similarly, it's often easier to answer questions like "How much of our next $10,000 should we spend on research, as opposed to advertising?" than to answer "Which is more important right now, research or advertising?"
- Do "Focusing" and other resonance checks. It's often useful to try on a perspective, hypothetically, and then pay attention to your intuition and bodily responses to refine your actual stance. For instance: (wildly asserts) "I bet if everyone wore uniforms there would be a fifty percent reduction in bullying." (pauses, listens to inner doubts) "Actually, scratch that—that doesn't seem true, now that I say it out loud, but there is something in the vein of reducing overt bullying, maybe?"
- Seek cruxes independently before anchoring on your partner's thoughts. This one is fairly straightforward. It's also worth noting that if you're attempting to find disagreements in the first place (e.g. in order to practice double cruxing with friends) this is an excellent way to start—give everyone the same ten or fifteen open-ended questions, and have everyone write down their own answers based on their own thinking, crystallizing opinions before opening the discussion.
Overall, it helps to keep the ideal of a perfect double crux in the front of your mind, while holding the realities of your actual conversation somewhat separate. We've found that, at any given moment, increasing the "double cruxiness" of a conversation tends to be useful, but worrying about how far from the ideal you are in absolute terms doesn't. It's all about doing what's useful and productive in the moment, and that often means making sane compromises—if one of you has clear cruxes and the other is floundering, it's fine to focus on one side. If neither of you can find a single crux, but instead each of you has something like eight co-cruxes of which any five are sufficient, just say so and then move forward in whatever way seems best.
(Variant: a "trio" double crux conversation in which, at any given moment, if you're the least-active participant, your job is to squint at your two partners and try to model what each of them is saying, and where/why/how they're talking past one another and failing to see each other's points. Once you have a rough "translation" to offer, do so—at that point, you'll likely become more central to the conversation and someone else will rotate out into the squinter/translator role.)
Ultimately, each move should be in service of reversing the usual antagonistic, warlike, "win at all costs" dynamic of most disagreements. Usually, we spend a significant chunk of our mental resources guessing at the shape of our opponent's belief structure, forming hypotheses about what things are crucial and lobbing arguments at them in the hopes of knocking the whole edifice over. Meanwhile, we're incentivized to obfuscate our own belief structure, so that our opponent's attacks will be ineffective.
(This is also terrible because it means that we often fail to even find the crux of the argument, and waste time in the weeds. If you've ever had the experience of awkwardly fidgeting while someone spends ten minutes assembling a conclusive proof of some tangential sub-point that never even had the potential of changing your mind, then you know the value of someone being willing to say "Nope, this isn't going to be relevant for me; try speaking to that instead.")
If we can move the debate to a place where, instead of fighting over the truth, we're collaborating on a search for understanding, then we can recoup a lot of wasted resources. You have a tremendous comparative advantage at knowing the shape of your own belief structure—if we can switch to a mode where we're each looking inward and candidly sharing insights, we'll move forward much more efficiently than if we're each engaged in guesswork about the other person. This requires that we want to know the actual truth (such that we're incentivized to seek out flaws and falsify wrong beliefs in ourselves just as much as in others) and that we feel emotionally and socially safe with our partner, but there's a doubly-causal dynamic where a tiny bit of double crux spirit up front can produce safety and truth-seeking, which allows for more double crux, which produces more safety and truth-seeking, etc.
Pitfalls
First and foremost, it matters whether you're in the strong version of double crux (cooperative, consent-based) or the weak version (you, as an agent, trying to improve the conversational dynamic, possibly in the face of direct opposition). In particular, if someone is currently riled up and conceives of you as rude/hostile/the enemy, then saying something like "I just think we'd make better progress if we talked about the underlying reasons for our beliefs" doesn't sound like a plea for cooperation—it sounds like a trap.
So, if you're in the weak version, the primary strategy is to embody the question "What do you see that I don't?" In other words, approach from a place of explicit humility and good faith, drawing out their belief structure for its own sake, to see and appreciate it rather than to undermine or attack it. In my experience, people can "smell it" if you're just playing at good faith to get them to expose themselves; if you're having trouble really getting into the spirit, I recommend meditating on times in your past when you were embarrassingly wrong, and how you felt prior to realizing it compared to after realizing it.
(If you're unable or unwilling to swallow your pride or set aside your sense of justice or fairness hard enough to really do this, that's actually fine; not every disagreement benefits from the double-crux-nature. But if your actual goal is improving the conversational dynamic, then this is a cost you want to be prepared to pay—going the extra mile, because a) going what feels like an appropriate distance is more often an undershoot, and b) going an actually appropriate distance may not be enough to overturn their entrenched model in which you are The Enemy. Patience- and sanity-inducing rituals recommended.)
As a further tip that's good for either version but particularly important for the weak one, model the behavior you'd like your partner to exhibit. Expose your own belief structure, show how your own beliefs might be falsified, highlight points where you're uncertain and visibly integrate their perspective and information, etc. In particular, if you don't want people running amok with wrong models of what's going on in your head, make sure you're not acting like you're the authority on what's going on in their head.
Speaking of non-sequiturs, beware of getting lost in the fog. The very first step in double crux should always be to operationalize and clarify terms. Try attaching numbers to things rather than using misinterpretable qualifiers; try to talk about what would be observable in the world rather than how things feel or what's good or bad. In the school uniforms example, saying "uniforms make students feel better about themselves" is a start, but it's not enough, and going further into quantifiability (if you think you could actually get numbers someday) would be even better. Often, disagreements will "dissolve" as soon as you remove ambiguity—this is success, not failure!
Finally, use paper and pencil, or whiteboards, or get people to treat specific predictions and conclusions as immutable objects (if you or they want to change or update the wording, that's encouraged, but make sure that at any given moment, you're working with a clear, unambiguous statement). Part of the value of double crux is that it's the opposite of the weaselly, score-points, hide-in-ambiguity-and-look-clever dynamic of, say, a public political debate. The goal is to have everyone understand, at all times and as much as possible, what the other person is actually trying to say—not to try to get a straw version of their argument to stick to them and make them look silly. Recognize that you yourself may be tempted or incentivized to fall back to that familiar, fun dynamic, and take steps to keep yourself in "scout mindset" rather than "soldier mindset."
Algorithm
This is the double crux algorithm as it currently exists in our handbook. It's not strictly connected to all of the discussion above; it was designed to be read in context with an hour-long lecture and several practice activities (so it has some holes and weirdnesses) and is presented here more for completeness and as food for thought than as an actual conclusion to the above.
1. Find a disagreement with another person
- A case where you believe one thing and they believe the other
- A case where you and the other person have different confidences (e.g. you think X is 60% likely to be true, and they think it’s 90%)
2. Operationalize the disagreement
- Define terms to avoid getting lost in semantic confusions that miss the real point
- Find specific test cases—instead of (e.g.) discussing whether you should be more outgoing, instead evaluate whether you should have said hello to Steve in the office yesterday morning
- Wherever possible, try to think in terms of actions rather than beliefs—it’s easier to evaluate arguments like “we should do X before Y” than it is to converge on “X is better than Y.”
3. Seek double cruxes
- Seek your own cruxes independently, and compare with those of the other person to find overlap
- Seek cruxes collaboratively, by making claims (“I believe that X will happen because Y”) and focusing on falsifiability (“It would take A, B, or C to make me stop believing X”)
4. Resonate
- Spend time “inhabiting” both sides of the double crux, to confirm that you’ve found the core of the disagreement (as opposed to something that will ultimately fail to produce an update)
- Imagine the resolution as an if-then statement, and use your inner sim and other checks to see if there are any unspoken hesitations about the truth of that statement
5. Repeat!
Conclusion
We think double crux is super sweet. To the extent that you see flaws in it, we want to find them and repair them, and we're currently betting that repairing and refining double crux is going to pay off better than try something totally different. In particular, we believe that embracing the spirit of this mental move has huge potential for unlocking people's abilities to wrestle with all sorts of complex and heavy hard-to-parse topics (like existential risk, for instance), because it provides a format for holding a bunch of partly-wrong models at the same time while you distill the value out of each.
Comments appreciated; critiques highly appreciated; anecdotal data from experimental attempts to teach yourself double crux, or teach it to others, or use it on the down-low without telling other people what you're doing extremely appreciated.
- Duncan Sabien
[1]One reason good faith is important is that even when people are "wrong," they are usually partially right—there are flecks of gold mixed in with their false belief that can be productively mined by an agent who's interested in getting the whole picture. Normal disagreement-navigation methods have some tendency to throw out that gold, either by allowing everyone to protect their original belief set or by replacing everyone's view with whichever view is shown to be "best," thereby throwing out data, causing information cascades, disincentivizing "noticing your confusion," etc.
The central assumption is that the universe is like a large and complex maze that each of us can only see parts of. To the extent that language and communication allow us to gather info about parts of the maze without having to investigate them ourselves, that's great. But when we disagree on what to do because we each see a different slice of reality, it's nice to adopt methods that allow us to integrate and synthesize, rather than methods that force us to pick and pare down. It's like the parable of the three blind men and the elephant—whenever possible, avoid generating a bottom-line conclusion until you've accounted for all of the available data.
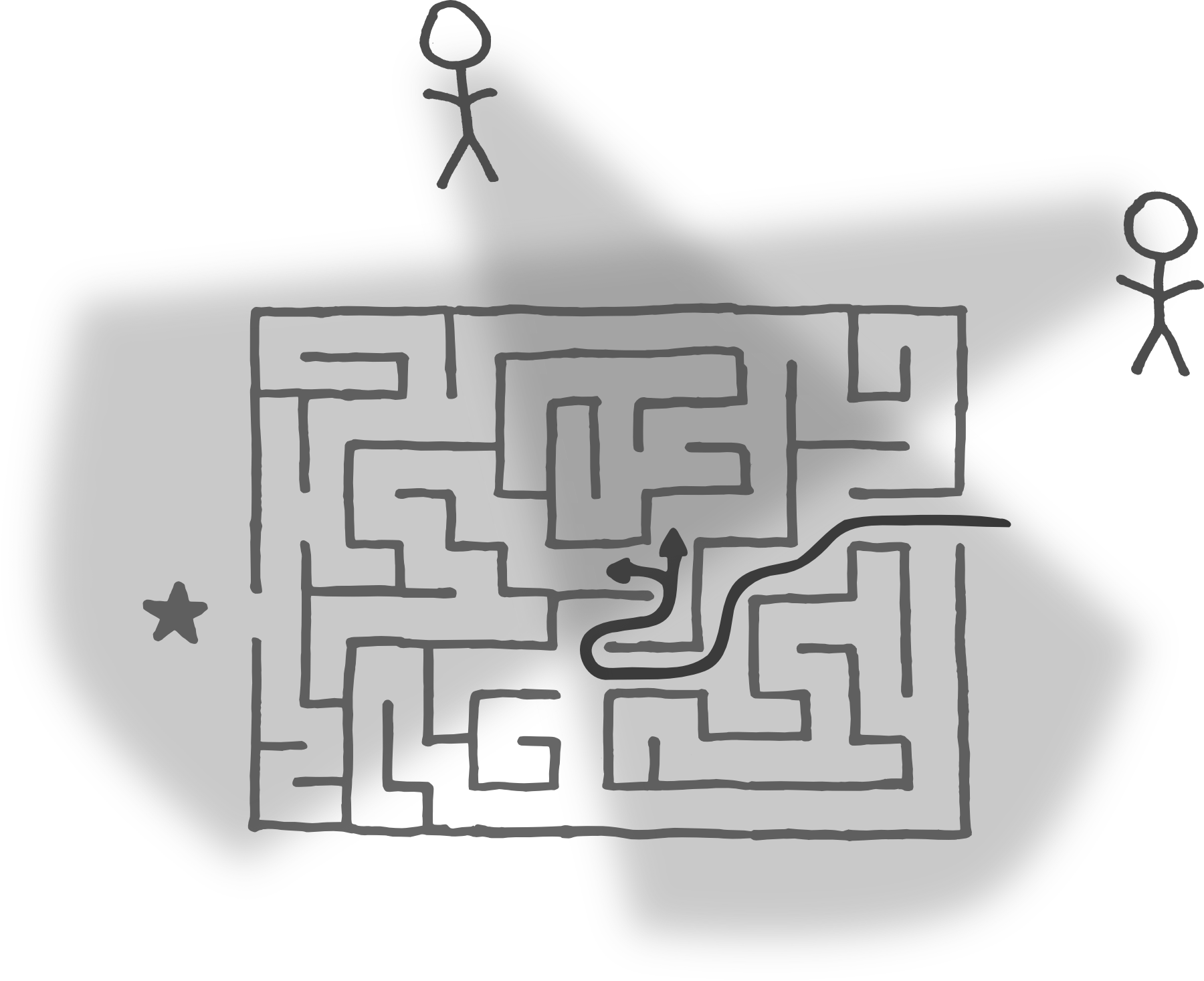
The agent at the top mistakenly believes that the correct move is to head to the left, since that seems to be the most direct path toward the goal. The agent on the right can see that this is a mistake, but it would never have been able to navigate to that particular node of the maze on its own.