Seeking Power is Often Robustly Instrumental in MDPs relates the structure of the agent's environment (the 'Markov decision process (MDP) model') to the tendencies of optimal policies for different reward functions in that environment ('instrumental convergence'). The results tell us what optimal decision-making 'tends to look like' in a given environment structure, formalizing reasoning that says e.g. that most agents stay alive because that helps them achieve their goals.
Several people have claimed to me that these results need subjective modelling decisions. For example, ofer wrote:
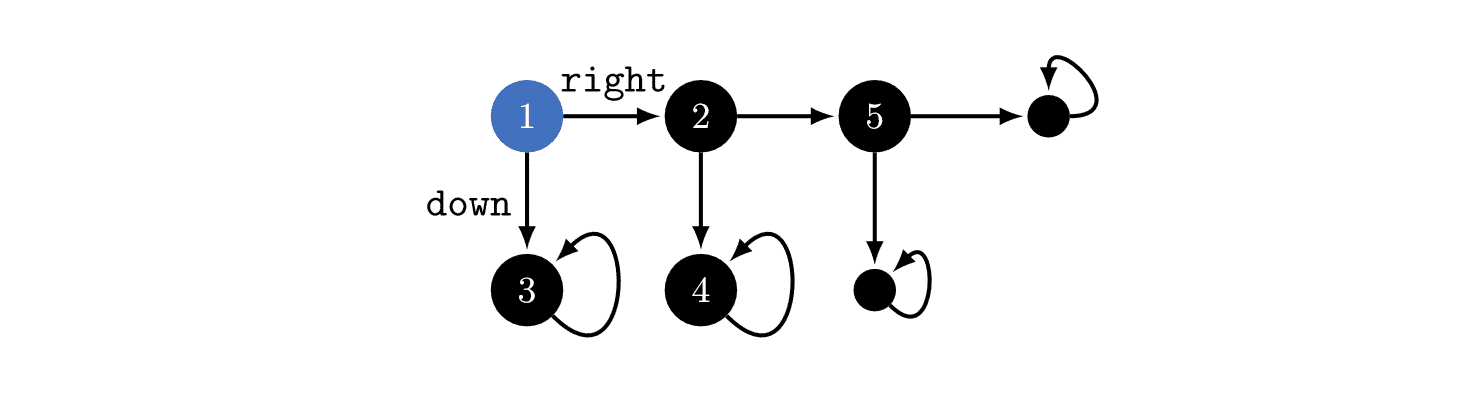
I think using a well-chosen reward distribution is necessary, otherwise POWER depends on arbitrary choices in the design of the MDP's state graph. E.g. suppose the student [in a different example] writes about every action they take in a blog that no one reads, and we choose to include the content of the blog as part of the MDP state. This arbitrary choice effectively unrolls the state graph into a tree with a constant branching factor (+ self-loops in the terminal states) and we get that the POWER of all the states is equal.
In the above example, you could think about the environment as in the above image, or you could imagine that state '3' is actually a million different states which just happen to seem similar to us! If that were true, then optimal policies would tend to go , since that would give the agent millions of choices about where it ends up. Therefore, the power-seeking theorems depend on subjective modelling assumptions.
I used to think this, but this is wrong. The MDP model is determined by the agent's implementation + the task's dynamics.
To make this point, let's back out to a more familiar MDP: Pac-Man.
When the discount rate is near 1, most reward functions avoid immediately dying to the ghost, because then they'd be stuck in a terminal state (the red-ghost-game-over state). But why can't the red ghost be equally well-modeled as secretly being 5 googolplex different terminal states?
An MDP model (technically, a rewardless MDP) is a tuple , where is the state space, is the action space, and is the (potentially stochastic) transition function which says what happens when the agent takes different actions at different states. has to be Markovian, depending only on the observed state and the current action, and not on prior history.
Whence cometh this MDP model? Thin air? Is it just a figment of our imagination, which we use to understand what the agent is doing as it learns a policy?
When we train a policy function in the real world, the function takes in an observation (the state) and outputs (a distribution over) actions. When we define state and action encodings, this implicitly defines an "interface" between the agent and the environment. The state encoding might look like "the set of camera observations" or "the set of Pac-Man game screens", and actions might be numbers 1-10 which are sent to actuators, or to the computer running the Pac-Man code, etc.
(In the real world, the computer simulating Pac-Man may suffer a hardware failure / be hit by a gamma ray / etc, but I don't currently think these are worth modelling over the timescales over which we train policies.)
Suppose that for every state-action history, what the agent sees next depends only on the currently observed state and the most recent action taken. Then the environment is Markovian (transition dynamics only depend on what you do right now, not what you did in the past) and fully observable (you can see the whole state all at once), and the agent encodings have defined the MDP model.
In Pac-Man, the MDP model is uniquely defined by how we encode states and actions, and the part of the real world which our agent interfaces with. If you say "maybe the red ghost is represented by 5 googolplex states", then that's a falsifiable claim about the kind of encoding we're using.
That's also a claim that we can, in theory, specify reward functions which distinguish between 5 googolplex variants of red-ghost-game-over. If that were true, then yes - optimal policies really would tend to "die" immediately, since they'd have so many choices.
The "5 googolplex" claim is both falsifiable and false. Given an agent architecture (specifically, the two encodings), optimal policy tendencies are not subjective. We may be uncertain about the agent's state- and action-encodings, but that doesn't mean we can imagine whatever we want.
(I think that the same point holds for other environment types, like POMDPs.)



To clarify: when I say that taking over the world is "instrumentally convergent", I mean that most objectives incentivize it. If you mean something else, please tell me. (I'm starting to think there must be a serious miscommunication somewhere if we're still disagreeing about this?)
So we can't set the 'arbitrary' part aside - instrumentally convergent means that the incentives apply across most reward functions - not just for one. You're arguing that one reward function might have that incentive. But why would most goals tend to have that incentive?
This doesn't make sense to me. We assumed the agent is Cartesian-separated from the universe, and its actions magically make strings appear somewhere in the world. How could humans interfere with it? What, concretely, are the "risks" faced by the agent?
(Technically, the agent's goals are defined over the text-state, and you can assign high reward to text-states in which people bought stuff. But the agent doesn't actually have goals over the physical world as we generally imagine them specified.)
This statement is vacuous, because it's true about any possible string.
----
The original argument given for instrumental convergence and power-seeking is that gaining resources tends to be helpful for most objectives (this argument isn't valid in general, but set that aside for now). But even that's not true here. The problem is that the 'text-string-world' model is framed in a leading way, which is suggestive of the usual power-seeking setting (it's representing the real world and it's complicated, there must be instrumental convergence), even though it's structurally a whole different beast.
Objective functions induce preferences over text-states (with a "what's the world look like?" tacked on). The text-state the agent ends up in is, by your assumption, determined by the text output of the agent. Nothing which happens in the world expands or restrict's the agent's ability to output text. So there's no particular reason for optimal policies to tend to output strings that induce text-histories in which the world contains a disempowered human civilization.
Another way to realize that optimal policies don't have this tendency is that optimal policy tendencies are invariant to model isomorphism, and, again, this environment is literally isomorphic to
If it were true that optimal agents tend to "take over the world" in the 'real-world' model, then it would be true in the sequential string output model, which is absurd.
I know I've said this several times, but this is a knock-down argument, and you haven't engaged with it. If you take a piece of paper and draw out a model for the following environment - it will be a regular tree:
You may already know that, because you quickly pointed out that POWER is constant. But then why do you claim that most reward functions are attracted to certain branches of the tree, given that regularity? And if you aren't claiming that, what do you mean by instrumental convergence?