Comment Permalink

Refering to this:

"Simply knowing the fact that the entropy is concave down tells us that to maximize entropy we should split it up as evenly as possible - each side has a 1/4 chance of showing."

Ok, that's fine for discrete events, but what about continuous ones? That is, how do I choose a prior for real-valued parameters that I want to know about? As far as I am aware, MAXENT doesn't help me at all here, particularly as soon as I have several parameters, and no preferred parameterisation of the problem. I know Jaynes goes on about how continuous distributions make no sense unless you know the sequence whose limit you took to get there, in which case problem solved, but I have found this most unhelpful in solving real problems where I have no preference for any particular sequence, such as in models of fundamental physics.

Manfred11y00

Well, you can still define information entropy for probability density functions - though I suppose if we ignore Jaynes we can probably get paradoxes if we try. In fact, I'm pretty sure just integrating p*Log(p) is right. There's also a problem if you want to have a maxent prior over the integers or over the real numbers; that takes us into the realm of improper priors.

I don't know as much as I should about this topic, so you may have to illustrate using an example before I figure out what you mean.

See in context

17 Putting in the Numbers

by Manfred

30th Jan 2014

4 min read

17

Followup To: Foundations of Probability

In the previous post, we reviewed reasons why having probabilities is a good idea. These foundations defined probabilities as numbers following certain rules, like the product rule and the rule that mutually exclusive probabilities sum to 1 at most. These probabilities have to hang together as a coherent whole. But just because probabilities hang together a certain way, doesn't actually tell us what numbers to assign.

I can say a coin flip has P(heads)=0.5, or I can say it has P(heads)=0.999; both are perfectly valid probabilities, as long as P(tails) is consistent. This post will be about how to actually get to the numbers.

If the probabilities aren't fully determined by our desiderata, what do we need to determine the probabilities? More desiderata!

Our final desideratum is motivated by the perspective that our probability is based on some state of information. This is acknowledged explicitly in Cox's scheme, but is also just a physical necessity for any robot we build. Thus we add our new desideratum: Assign probabilities that are consistent with the information you have, but don't make up any extra information. It turns out this is enough to let us put numbers to the probabilities.

In its simplest form, this desideratum is a symmetry principle. If you have the exact same information about two events, you should assign them the same probability - giving them different probabilities would be making up extra information. So if your background information is "Flip a coin, the mutually exclusive and exhaustive probabilities are heads and tails," there is a symmetry between the labels "heads" and "tails," which given our new desideratum lets us assign each P=0.5.

Sometimes, though, we need to pull out the information theory. Using the fact that it doesn't produce information to split the probabilities up differently, we can specify something called "information entropy" (For more thoroughness, see chapter 11 of Jaynes). The entropy of a probability distribution is a function that measures how uncertain you are. If I flip a coin and don't know about the outcome, I have one bit of entropy. If I flip two coins, I have two bits of entropy. In this way, the entropy is like the amount of information you're "missing" about the coin flips.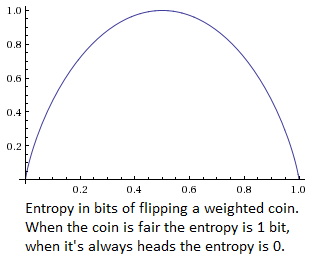 Entropy of weighted coin

The mathematical expression for information entropy is that it's the sum of each probability multiplied by its log. Entropy = -Sum( P(x)·Log(P(x)) ), where the events x are mutually exclusive. Assigning probabilities is all about maximizing the entropy while obeying the constraints of our prior information.

Suppose we roll a 4-sided die. Our starting information consists of our knowledge that there are sides numbered 1 to 4 (events 1, 2, 3, and 4 are exhaustive), and the die will land on just one of these sides (they're mutually exclusive). This let's us write our information entropy as -P(1)·Log(P(1)) - P(2)·Log(P(2)) - P(3)·Log(P(3)) - P(4)·Log(P(4)).

Finding the probabilities is a maximization problem, subject to the constraints of our prior information. For the simple 4-sided die, our information just says that the probabilities have to add to 1. Simply knowing the fact that the entropy is concave down tells us that to maximize entropy we should split it up as evenly as possible - each side has a 1/4 chance of showing.

That was pretty commonsensical. To showcase the power of maximizing information entropy, we can add an extra constraint.

If we have additional knowledge that the average roll of our die is 3, then we want to maximize -P(1)·Log(P(1)) - P(2)·Log(P(2)) - P(3)·Log(P(3)) - P(4)·Log(P(4)), given that the sum is 1 and the average is 3. We can either plug in the constraints and set partial derivatives to zero, or we can use a maximization technique like Lagrange multipliers.

When we do this (again, more details in Jaynes ch. 11), it turns out the the probability distribution is shaped like an exponential curve. Which was unintuitive to me - my intuition likes straight lines. But it makes sense if you think about the partial derivative of the information entropy: 1+Log(P) = [some Lagrange multiplier constraints]. The steepness of the exponential controls how shifted the average roll is.

The need for this extra desideratum has not always been obvious. People are able to intuitively figure out that a fair coin lands heads with probability 0.5. Seeing that their intuition is so useful, some people include that intuition as a fundamental part of their method of probability. The counter to this is to focus on constructing a robot, which only has those intuitions we can specify unambiguously.

Another alternative to assigning probabilities based on maximum entropy is to pick a standard prior and use that. Sometimes this works wonderfully - it would be silly to rederive the binomial distribution every time you run into a coin-flipping problem. But sometimes people will use a well-known prior even if it doesn't match the information they have, just because their procedure is "use a well-known prior." The only way to be safe from that mistake and from interminable disputes over "which prior is right" is to remember that a prior is only correct insofar as it captures some state of information.

Next post, we will finally get to the problem of logical uncertainty, which will shake our foundations a bit. But I really like the principle of not making up information - even a robot that can't do hard math problems can aspire to not make up information.

Part of the sequence Logical Uncertainty

Previous Post: Foundations of Probability

Next post: Logic as Probability

Personal Blog

17

Mentioned in

19Foundations of Probability

18Logic as Probability

New Comment

33 comments, sorted by

top scoring

Click to highlight new comments since: Today at 8:47 AM

[-]Oscar_Cunningham11y40

If we have additional knowledge that the average roll of our die is 3, then we want to maximize -P(1)·Log(P(1)) - P(2)·Log(P(2)) - P(3)·Log(P(3)) - P(4)·Log(P(4)), given that the sum is 1 and the average is 3. We can either plug in the constraints and set partial derivatives to zero, or we can use a maximization technique like Lagrange multipliers.

I've never been able to understand this.

Surely the correct course of action in this situation is to have a prior for the possible biases of the die, say the uniform prior on {x in R^4 : x1+x2+x3+x4=1, xi>=0 for all i}, and then update Bayesianly by restricting to the subset where the average is 3. Then to find the distribution for the outcomes of the die we integrate over this.

I'm pretty sure this doesn't give the same distribution as maxent, and I can't think of a prior that would. (I think my suggested prior gives the "straight lines" distribution that you wanted!)

So when are each of these procedures appropriate? I agree that maxent is a good way to assign priors, but I think that when you have data you should use it by updating, rather than by remaking you prior.

[-][anonymous]11y50

I don't think there's anything that says a maximum entropy prior is what you get if you construct a maximum entropy prior for a weaker subset of assumptions, and then update based on the complement.

EDIT: Jaynes elaborates on the relationship between Bayes and maximum entropy priors here (warning, pdf).

[-]Manfred11y20

Okay, I have an answer for you.

In doing the Bayesian updating method, you assumed that the die has some weights, and that the die having different weights are events in event-space. This assumption is a very good one for a physical die, and the nature of the assumption is most obvious from the Kolmogorov and Savage perspectives.

Then, when translating the information that the expected roll was 5/2, you translated it as "the sum of weight 1 + 2 * weight 2 + 3 * weight 3 is equal to 5/2." (Note that this is not necessary! If you're symmetrically uncertain about the weights, the expected roll can still be 5/2. Frequentist intuitions are so sneaky :P )

What does the maximum entropy principle say if we give it that same information? The exact same answer you got! It maximizes entropy over those different possibilities in event-space, and the constraint that the weighted sum of the weights is 5/2 is interpreted in just the way you'd expect, leaving a straight line of possibilities in event-space with equal weights. Thus, maxent gives the same answer as Bayes' theorem for this question, and it certainly seems like it did so given the same information you used for Bayes' theorem.

Since it didn't give the same answer before, this means we're solving a different set of equations. Different equations means different information.

The state of information that I use in the post is different because we have no knowledge that the probabilities comes from some physical process with different weights. No physical events at all are entangled with the probabilities. It's obvious why this is unintuitive - any die has some physical weights underlying it. So calling our unknown number "the roll of a die" is actually highly misleading. My bad on that one - it looks like christopherj's concerns about the example being unrealistic were totally legit.

However, that doesn't mean that we'll never see our maximum entropy result in the physical world. Suppose that I started not knowing that the expected roll of the die was 5/2. And then someone offered to repeat not just "rolling the die," but to repeat experiments with equivalent states of knowledge many times. And then what they'll do is after 1000 repeats of experiments with the same state of knowledge, is if the average roll was really close to 5/2, they'll stop, but if the average roll wasn't 5/2 they'll try again until it is.

Since the probability given my state of knowledge is 1/3, I expect a repeat of many experiments with the same state of knowledge to be like a rolling a fair die many times, then only keeping ensembles with average 5/2. Then, if I look at this ensemble that represents your state of knowledge except for happening to have average roll 5/2, I will see a maximum entropy distribution of rolls. (proof left as an exercise :P ) This physical process encapsulates the information stated in the post, in a way that rolling a die whose weights are different physical events does not.

[-]Manfred11y00

I'm pretty sure this doesn't give the same distribution as maxent

Wanna check? :)

[-]Oscar_Cunningham11y60

I'll work in the easier case 1 dimension down. Say we have a die which rolls a 1, 2 or a 3, and we know it averages to 5/2.

Then {x in R^3 : x1+x2+x3=1, xi>=0 for all i} is an equilateral triangle, which we put an uniform distribution on. Then the points where the mean roll is 5/2 lie on a straight line from (1/4,0,3/4) to (0,1/2,1/2). By some kind of linearity argument the averages over this line (with the uniform weighting from our uniform prior) are just the average of (1/4,0,3/4) and (0,1/2,1/2). This gives (1/8,2/8,5/8).

On the other hand we know that maxent gives a geometric sequence. But (1/8,2/8,5/8) isn't geometric.

[-]Cyan11y60

This may help. Abstract:

The method of maximum entropy has been very successful but there are cases where it has either failed or led to paradoxes that have cast doubt on its general legitimacy. My more optimistic assessment is that such failures and paradoxes provide us with valuable learning opportunities to sharpen our skills in the proper way to deploy entropic methods. The central theme of this paper revolves around the different ways in which constraints are used to capture the information that is relevant to a problem. This leads us to focus on four epistemically different types of constraints. I propose that the failure to recognize the distinctions between them is a prime source of errors. I explicitly discuss two examples. One concerns the dangers involved in replacing expected values with sample averages. The other revolves around misunderstanding ignorance. I discuss the Friedman-Shimony paradox as it is manifested in the three-sided die problem and also in its original thermodynamic formulation.

[-]Manfred11y20

Thanks, that's interesting. But if we know that the expected roll is 2, then that must lie somewhere on the straight line between (1/2,0,1/2) and (0,1,0). This doesn't mean we should average those to claim that the correct distribution given that information is (1/4,1/2,1/4), rather than the uniform distribution!

I'll think about this some more - Cyan's link also goes into the problem a bit.

[-]Vaniver11y00

I know a handful of people who have built / are building PhDs on dealing with scoring approximation rules based on how they handle distributions that are sampled from all possible distributions that satisfy some characteristics. The impression I get is that the rabbit hole is pretty deep; I haven't read through it all but here are some places to start: Montiel: [1] [2], Hammond: [1] [2].

This doesn't mean we should average those to claim that the correct distribution given that information is (1/4,1/2,1/4), rather than the uniform distribution!

It seems to me that P1=(1/4,1/2,1/4) is "more robust" than P2=(1/3,1/3,1/3) in some way- suppose you remove y from x1 and add it proportionally to x2 and x3. The result would be closer to 2 for P1 than for P2, especially if y is a fraction of x1 rather than a flat amount.

But it also seems to me like having a uniform distribution across all possible distributions is kind of silly. Do I really think that (1/10,4/5,1/10) is just as likely as (1/3,1/3,1/3)? I suspect it's possible to have a prior which results in maxent posteriors, but it might be the case that the prior depends on what sort of update you provide (i.e. it only works when you know the variance, and not when you know the mean) and it might not exist for some updates.

[-]Manfred11y00

Well, "a uniform distribution across possible distributions" is kinda nonsense. There is a single correct distribution for our starting information, which is (1/3,1/3,1/3), the "distribution across possible distributions" is just a delta function there.

Any non-delta "distribution over distributions" is laden with some model of what's going on in the die, and is a distribution over parts of that model. Maybe there's some subtle effect of singling out the complete, uniform model rather than integrating over some ensemble.

[-]Vaniver11y00

There is a single correct distribution for our starting information, which is (1/3,1/3,1/3), the "distribution across possible distributions" is just a delta function there.

Whoa, you think the only correct interpretation of "there's a die that returns 1, 2, or 3" is to be absolutely certain that it's fair? Or what do you think a delta function in the distribution space means?

(This will have effects, and they will not be subtle.)

Any non-delta "distribution over distributions" is laden with some model of what's going on in the die, and is a distribution over parts of that model.

One of the classic examples of this is three interpretations of "randomly select a point from a circle." You could do this by selecting a angle for a radius uniformly, then selecting a point on that radius uniformly along its length. Or you could do those two steps, and then select a point along the associated chord uniformly at random. Or you could select x and y uniformly at random in a square bounding the circle, and reject any point outside the circle. Only the last one will make all areas in the circle equally likely- the first method will make areas near the center more likely and the second method will make areas near the edge more likely (if I remember correctly).

But I think that it generally is possible to reach consensus on what criterion you want (such as "pick a method such that any area of equal size has equal probability of containing the point you select.") and then it's obvious what sort of method you want to use. (There's a non-rejection sampling way to get the equal area method for the circle, by the way.) And so you probably need to be clever about how you parameterize your distributions, and what priors you put on those parameters, and eventually you do have hyperparameters that functionally have no uncertainty. (This is, for example, seeing a uniform as a beta(1/2,1/2), where you don't have a distribution on the 1/2s.) But I think this is a reasonable way to go about things.

[-]torekp11y20

One of the classic examples of this is three interpretations of "randomly select a point from a circle."

In a separate comment, Kurros worries about cases with "no preferred parameterisation of the problem". I have the same worry as both of you, I think. I guess I'm less optimistic about the resolution. The parameterization seems like an empirical rabbit that Jaynes and other descendants of the Principle of Insufficient Reason are trying to pull out of an a priori hat. (See also Seidenfeld .pdf) section 3 on re-partitioning the sample space.)

I'd appreciate it if someone could assuage - or aggravate - this concern. Preferably without presuming quite as much probability and statistics knowledge as Seidenfeld does (that one went somewhat over my head, toward the end).

[-]alex_zag_al11y00

Whoa, you think the only correct interpretation of "there's a die that returns 1, 2, or 3" is to be absolutely certain that it's fair? Or what do you think a delta function in the distribution space means?

I haven't been able to follow this whole thread of conversation, but I think it's pretty clear you're talking about different things here.

Obviously, the long-run frequency distribution of the die can be many different things. One of them, (1/3, 1/3, 1/3), represents fairness, and is just one among many possibilities.
Equally obviously, the probability distribution that represents rational expectations about the first flip is only one thing. Manfred claims that it's (1/3, 1/3, 1/3), which doesn't represent fairness. It could equally well represent being certain that it's biased to land on only one side every time, but you have no idea which side.

[-]Vaniver11y00

I think it's pretty clear you're talking about different things here.

I thought so too, which is why I asked him what he thought a delta function in the distribution space meant.

One of them, (1/3, 1/3, 1/3), represents fairness, and is just one among many possibilities.

Right; but putting a delta function there means you're infinitely certain that's what it is, because you give probability 0 to all other possibilities.

It could equally well represent being certain that it's biased to land on only one side every time, but you have no idea which side.

Knowing that the die is completely biased, but not which side it is biased towards, would be represented by three delta functions, at (1,0,0), (0,1,0), and (0,0,1), each with a coefficient of (1/3). This is very different from the uniform case and the delta at (1/3,1/3,1/3) case, as you can see by calculating the posterior distribution for observing that the die rolled a 1.

[-]alex_zag_al11y00

okay, and you were just trying to make sure that Manfred knows that all this probability-of-distributions speech you're speaking isn't, as he seems to think, about the degree-of-belief-in-my-current-state-of-ignorance distribution for the first roll. Gotcha.

[-]alex_zag_al11y00

Okay... but do we agree that the degree-of-belief distribution for the first roll is (1/3, 1/3, 1/3), whether it's a fair die or a completely biased in an unknown way die?

Because I'm pretty sure that's what Manfred's talking about when he says

There is a single correct distribution for our starting information, which is (1/3,1/3,1/3),

and I think him going on to say

the "distribution across possible distributions" is just a delta function there.

was a mistake, because you were talking about different things.

EDIT:

I thought so too, which is why I asked him what he thought a delta function in the distribution space meant.

Ah. Yes. Okay. I am literally saying only things that you know, aren't I. My bad.

[This comment is no longer endorsed by its author]Reply

[-]Manfred11y00

Whoa, you think the only correct interpretation of "there's a die that returns 1, 2, or 3" is to be absolutely certain that it's fair? Or what do you think a delta function in the distribution space means?

It's not about if the die is fair - my state of information is fair. Of that it is okay to be certain. Also, I think I figured it out - see my recent reply to Oscar's parent comment.

[-]Kurros11y20

Refering to this:

"Simply knowing the fact that the entropy is concave down tells us that to maximize entropy we should split it up as evenly as possible - each side has a 1/4 chance of showing."

[-]Manfred11y00

I don't know as much as I should about this topic, so you may have to illustrate using an example before I figure out what you mean.

[-]Kurros11y10

Yeah I think integral( p*log(p) ) is it. The simplest problem is that if I have some parameter x to which I want to assign a prior (perhaps not over the whole real set, so it can be proper as you say -- the boundaries can be part of the maxent condition set), then via the maxent method I will get a different prior depending on whether I happen to assign the distribution over x, or x^2, or log(x) etc. That is, the prior pdf obtained for one parameterisation is not related to the one obtained for a different parameterisation by the correct transformation rule for probability density functions; that is, they contain logically different information. This is upsetting if you have no reason to prefer one parameterisation or another.

In the simplest case where you have no constraints except the boundaries, and maybe expect to get a flat prior (I don't remember if you do when there are boundaries... I think you do in 1D at least) then it is most obvious that a prior flat in x contains very different information to one flat in x^2 or log(x).

[-]alex_zag_al11y00

According to Jaynes, it's actually not - I don't have the page number on me, unfortunately. But the way he does it is by discretizing the space of possibilities, and taking the limit as the number of discrete possibilities goes to infinity. It's not the limit of the entropy H, since that goes to infinity, it's the limit of H - log(n). It turns out to be a little different from integrating p*Log(p).

[-]christopherj11y10

If I had a die which rolled an average of 3, my expectation for the individual probabilities would depend on my priors for why the die might be biased. For example, a die that never landed on 6 but landed on the other numbers equally, would average to 3 and be an excellent cheater's die. A die with a slightly increased probability to roll 1 would be a good candidate for manufacturer's defect. Could I truly have no priors on how a die came to be biased?

Edit: I just realized that I put the wrong number of sides on my die, since you were talking about a 4 sided die.

[-]Manfred11y20

You could if you were the robot we are constructing.

But yes, if you are a human you'll have some complicated information about how dice work. If you want to put this knowledge aside and see things from the robot's perspective, you might try replacing "die" with "object 253," "the die lands on side 1" with "event 759," and so on.

[-]christopherj11y-10

But words have meaning -- you shouldn't neglect that a "die" is a "3-dimensional object with n sides, usually designed such that each has equal probability of ending up when rolled". My objection would vanish if instead of a die it were a "random number generator returning integers from 1 to 4 with an average of 3"

In this case, the generator has an unknown distribution biased in some way toward the higher numbers. This is a problem because it is highly unlikely that my estimate of the probabilities matches the actual probabilities, and furthermore someone else might know the actual probabilities and be able to win bets against me.

[-][anonymous]11y10

So excited for this sequence. Keep it up!

[-]alex_zag_al11y00

In my experience with Bayesian biostatisticians, they don't talk much about the information a prior represents. But they're also not just using common ones. They talk a lot about its "properties" - priors with "really nice properties". As for as I can tell, they mean two things:

Computational properties
The way the distribution shifts as you get evidence. They think about this in a lot of detail, and they like priors that lead to behavior they think is reasonable.

I think this amounts to the same thing. The way they think and infer about the problem is determiend by their information. So, when they create a robot that thinks and infers in the same way, they are creating one with the same information as they have.

But, as a procedure for creating a prior that represents your information, it's very different from Jaynes's procedure. Jaynes's procedure being, stating your prior information very precisely, and then finding symmetries or constraints for maximum entropy I guess.

I'm very happy you're writing about logical uncertainty btw, it's been on my mind a lot lately.

[-][anonymous]11y00

I'm very happy you're writing about this, it's been on my mind a lot lately. Maximum entropy and logical uncertainty both.

[This comment is no longer endorsed by its author]Reply

[-]christopherj11y-20

OK, suppose that I tell your robot that a random number generator produces integers from 1 to 4. It dutifully calculates the maximum entropy, 1/4 chance for each. Now suppose that I tell it that a random number generator produces integers from 1 to 4, with an average value of 2.5. Now, though this is consistent with the original maximum entropy, the maximum entropy of the constraints (P1 + P2 + P3 + P4 = 1 and average = 2.5) will be an exponential distribution much like your distribution when the average was 3.

If your robot always calculates the maximum entropy distribution given constraints, it cannot instead take information as evidence of its previous hypothesis.

Me: What do you think is the distribution of this random number generator which returns integers from 1 to 4?

Robot: P=0.25 for each, because that is maximum entropy

Me: Guess what? The average value is 2.5, exactly as you predicted!

Robot: Excellent. My new prediction is that the distribution is exponential, instead of all 0.25, because that is now maximum entropy.

[This comment is no longer endorsed by its author]Reply

[-]Manfred11y30

e^0 is also exponential.

[-]christopherj11y00

e^0 is not the exponential you told your robot to choose in that situation.

[This comment is no longer endorsed by its author]Reply

[-]christopherj11y00

The robot doesn't care about your irrelevant technicality, it cares about maximum entropy. e^0 is exponential, but it is not the maximum entropy distribution with a given mean. In this case, it is Pr(X=x_k) = C*r^(x_k) for k = 1,2,3,4 where the positive constants C and r can be determined by the requirements that the sum of all the probabilities must be 1 and the expected value must be 2.5.

Just because I didn't actually write the formula doesn't mean it doesn't exist or you can replace it with any formula you like. So if the robot works as described, this is what the robot will update its expected probabilities to upon learning that the mean is 2.5, and not 2.5*e^0 because it would be convenient for you.

This is why many of us are terrified of the Singularity, because the author of a program seldom anticipates its actual result. What's even more terrifying is that this should have been obvious to you, as you gave an example as a strength of your idea of when the mean was 3.0. Why are you upset that I pointed out the consequences when the mean was 2.5? Instead of acknowledging the fact, you entirely forget what you told your robot to do and blurt out a misleading technicality?

[This comment is no longer endorsed by its author]Reply

[-]gjm11y30

Allow me to explain less snarkily and more directly than Manfred.

As you correctly observe, the maximum-entropy probability on {1,2,3,4} with any given mean is one that gives k (k=1,2,3,4) probability A.r^k for some A,r, and these parameters are uniquely determined by the requirement that the probabilities sum to 1 and that the resulting mean should be the given one.

In the particular case where the mean is 2.5, the specific values in question are A=1/4 and r=1.

This distribution can be described as exponential, if you insist -- but it also happens to be the same uniform distribution that's maximum-entropy without knowing the mean.

So the inconsistency you seemed to be suggesting -- of an entropy-maximizing Bayesian robot choosing one distribution on the basis of maxent, and then switching to a different one on having one property of that distribution confirmed -- is not real. On learning that the mean is 2.5 as it already guessed, the robot does not switch to a different distribution.

[EDITED: minor tweaks for clarity.]

[-]christopherj11y20

It just occurred to me that I really ought to check whether I ought to check that it was in fact different rather than going, "what are the odds that out of all the possibilities that equation happens to be the uniform distribution?". Guess I should have done that before posting.

It also occurs to me now, that I didn't even have to calculate out the equation (which I thought was too much effort for a "someone is wrong on the internet"), and could just plug in the values ... and in fact I even already did that when finding the uniform distribution and its mean.

This post sponsored by "When someone is wrong on the internet, it's sometimes you"

[-]Manfred11y00

Pr(X=xk) = C*r^(xk) for k = 1,2,3,4 where the positive constants C and r can be determined by the requirements that the sum of all the probabilities must be 1 and the expected value must be 2.5.

r^x = e^kx, where e^k=r. So. Would you like to wager whether r=1?

Moderation Log