I have been reading about money pump arguments for justifying the VNM axioms, and I'm already stuck at the part where Gustafsson justifies acyclicity. Namely, he seems to assume that agents have no memory. Why does this make sense?[1] To elaborate:
The standard money pump argument looks like this.
Let's assume (1) , and that we have a souring of such that it satisfies (2) , and (3) [2]. Then if you start out with , at each of the nodes you'll trade for , , and , so you'll end up paying for getting what you started with.
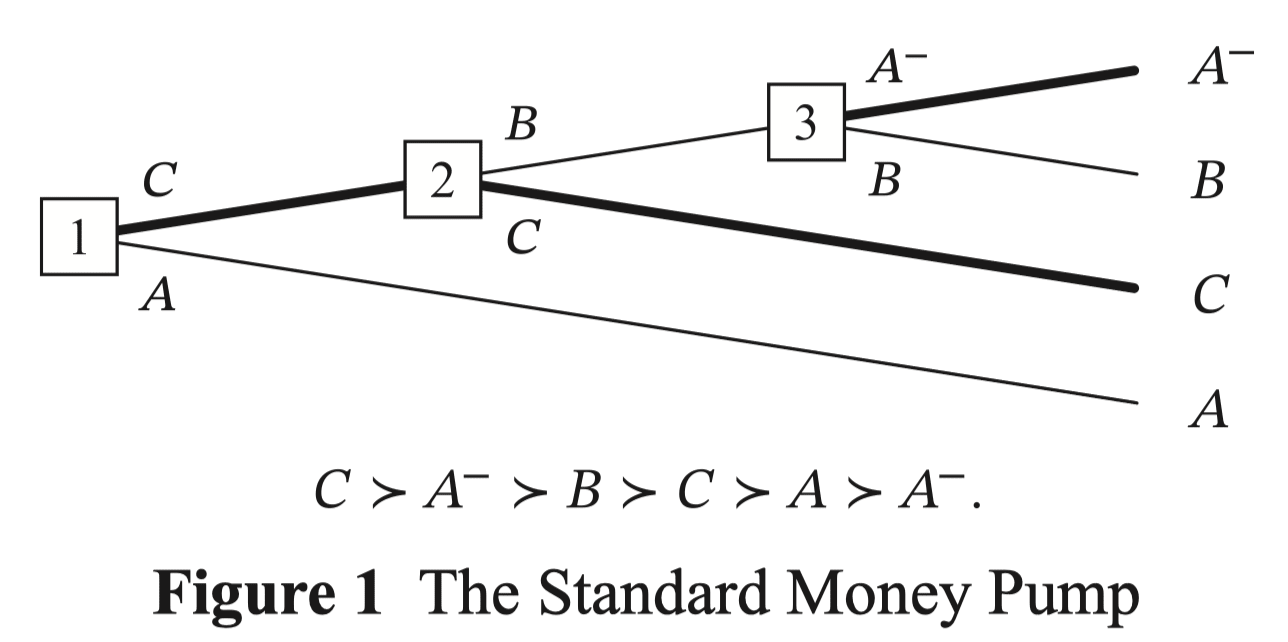
This makes sense, until you realize that the agent here implicitly believes that their current choice is the last choice they'll ever make, i.e. they're behaving myopically.
Notice that without such restriction, there is the obvious strategy of: "look at the full tree, only pick leaf nodes that aren't in the state of having been money pumped, and stick to the plan of only reaching that node."
- In practice, this looks fairly reasonable: "Yes, I do in fact prefer onions to pineapples to mushrooms to onions on my pizza. So what? If I know that you're trying to money pump me, I'll just refuse the trade. I may end up locally choosing options that I disprefer, but I don't care since there is no rule that I must be myopic, and I will end up with a preferred outcome at the end."
I'd say myopic agents are unnatural (as Gustafsson notes) because we want to assume the agent has full knowledge of all the trades that are available to them. Otherwise a defect (i.e. getting money-pumped) could be associated not necessarily with their preferences, but with their incomplete knowledge of the world.
So he proceeds to consider less restrictive agents such as sophisticated[3] and minimally sophisticated[4] agents, for which the above setup fails - but there exist modifications that still make money pump possible as long as they have cyclic preferences.
However, all of these agents still follow one critical assumption:
Decision-Tree Separability: The rational status of the options at a choice node does not depend on other parts of the decision tree than those that can be reached from that node.
This means that agents have no memory (this ruling out my earlier strategy of "looking at the final outcome and committing to a plan"). This still seems very restrictive.
Can anyone give a better explanation as to why such money pump arguments (with very unrealistic assumptions) are considered good arguments for the normativity of acyclic preferences as a rationality principle?
- ^
To be clear, I'm not claiming "... therefore I think cyclic preferences are actually okay." I understand that the point of formalizing money pump arguments is to capture our intuitive notion of something being wrong when someone has cyclic preferences. I'm more questioning the formalism and its assumptions.
- ^
Note (3) doesn't follow from (2), because here is a general binary relation. We are trying to derive all the nice properties like acyclicity, transitivity and such.
- ^
Agents that can, starting from their current node, use backwards induction to locally take the most preferred path.
- ^
A modification of sophisticated agents such that it no longer needs to predict it will act rationally in nodes that can only be reached by irrational decisions.
Yes, it is unrealistic. The problem is that no-one has devised something more complex that everyone agrees on, leaving EU (expected utility) theory as the only Schelling point in the field.
With the VNM axioms (and all similar setups for deriving utility functions), there are no decision trees and no history. Decisions are one-off, and assumed to be determined by a preference relation which considers only the two options presented. There is no past and no future for the agent making these "decisions".
I put quote marks there because a decision in the real world leads to actions which change the world in some way according to the agent's intentions. Actions are followed by more decisions and actions, and so on. All of this is excluded from the VNM framework, in which there are no "decisions", only preferences. EU theory hardly merits being called a decision theory, for all that the SEP article on decision theory talks almost exclusively about EU and only dips a toe into the waters of sequential decisions, recording how philosophers have made rather heavy weather even of the simple story of Ulysses and the sirens.
If you try to extend the VNM framework to the real world of sequential decisions and strategies, you end up making the "outcomes" be all possible configurations of the whole of your future light-cone. The preference relation is defined on all pairs of these configurations. The agent's "actions" are all the possible sequences of its individual actions. But who can know how their actions will affect their entire future light-cone, or what actions will become available to them in their far future?
I do not think that EU theory can usefully be extended in this way. It is a spherical cow too far.