An interesting experiment: researchers set up a wheel on a ramp with adjustable weights. Participants in the experiment then adjust the weights to try and make the wheel roll down the ramp as quickly as possible. The participants go one after the other, each with a limited number of attempts, each passing their data and/or theories to the next person in line, with the goal of maximizing the speed at the end. As information accumulates “from generation to generation”, wheel speeds improve.
This produced not just one but two interesting results.
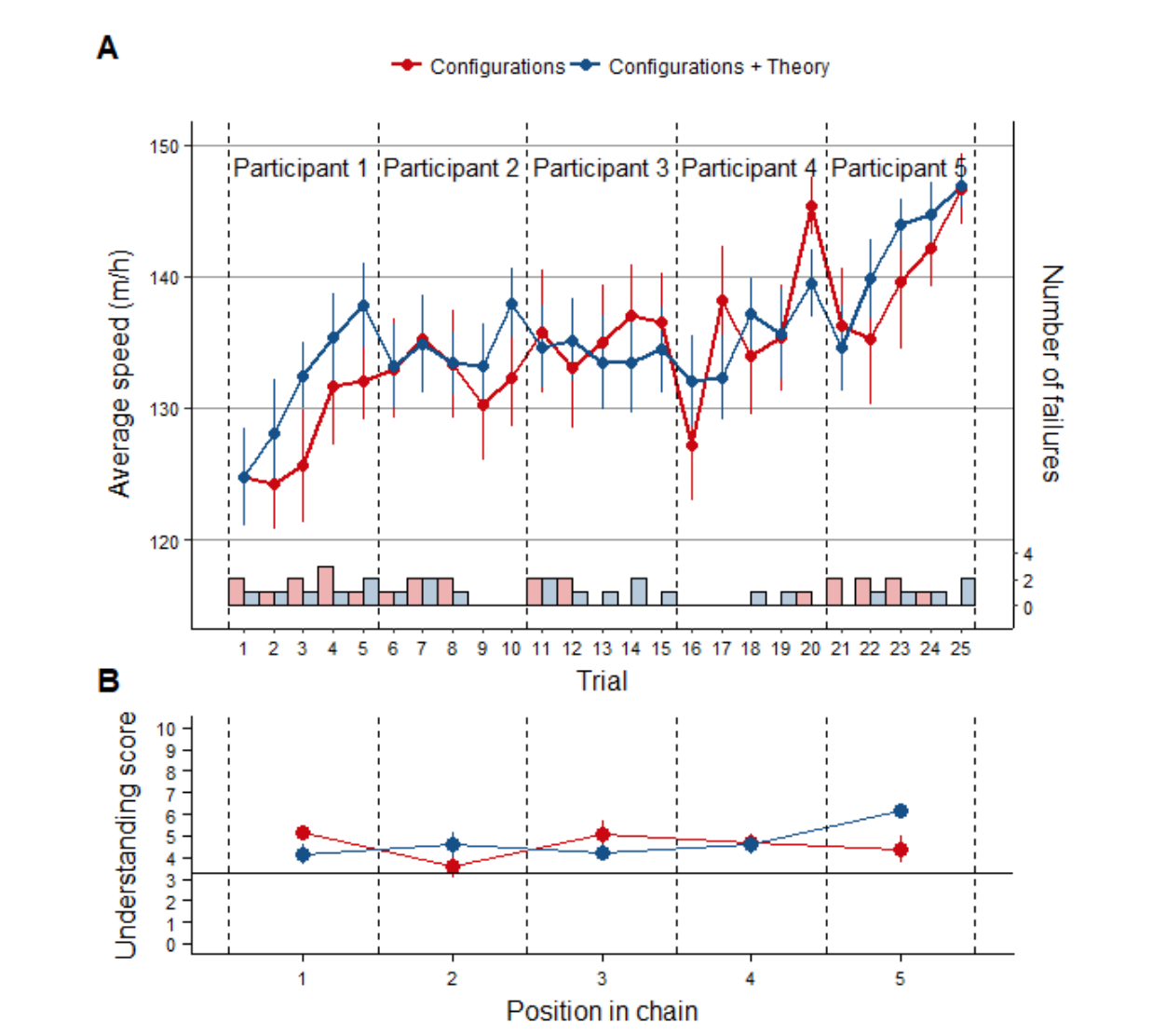
First, after each participant’s turn, the researchers asked the participant to predict how fast various configurations would roll. Even though wheel speed increased from person to person, as data accumulated, their ability to predict how different configurations behave did not increase. In other words, performance was improving, but understanding was not.
Second, participants in some groups were allowed to pass along both data and theories to their successors, while participants in other groups were only allowed to pass along data. Turns out, the data-only groups performed better. Why? The authors answer:
... participants who inherited an inertia- or energy- related theory showed skewed understanding patterns. Inheriting an inertia-related theory increased their understanding of inertia, but decreased their understanding of energy…
And:
... participants’ understanding may also result from different exploration patterns. For instance, participants who received an inertia-related theory mainly produced balanced wheels (Fig. 3F), which could have prevented them from observing the effect of varying the position of the wheel’s center of mass.
So, two lessons:
- Iterative optimization does not result in understanding, even if the optimization is successful.
- Passing along theories can actually make both understanding and performance worse.
So… we should iteratively optimize and forget about theorizing? Fox not hedgehog, and all that?
Well… not necessarily. We’re talking here about a wheel, with weights on it, rolling down a ramp. Mathematically, this system just isn’t all that complicated. Anyone with an undergrad-level understanding of mechanics can just crank the math, in all of its glory. Take no shortcuts, double-check any approximations, do it right. It’d be tedious, but certainly not intractable. And then… then you’d understand the system.
What benefit would all this theory yield? Well, you could predict how different configurations would perform. You could say for sure whether you had found the best solution, or whether better configurations were still out there. You could avoid getting stuck in local optima. Y’know, all the usual benefits of actually understanding a system.
But clearly, the large majority of participants in the experiment did not crank all that math. They passed along ad-hoc, incomplete theories which didn’t account for all the important aspects of the system.
This suggests a valley of bad theory. People with no theory, who just iteratively optimize, can do all right - they may not really understand it, they may have to start from scratch if the system changes in some important way, but they can optimize reasonably well within the confines of the problem. On the other end, if you crank all the math, you can go straight to the optimal solution, and you can predict in advance how changes will affect the system.
But in between those extremes, there’s a whole lot of people who are really bad at physics and/or math and/or theorizing. Those people would be better off just abandoning their theories, and sticking with dumb iterative optimization.


I'm curious how the complexity of the system affects the results. If someone hasn't learned at least a little physics - a couple college classes' worth or the equivalent - then the probability of inventing/discovering enough of the principles of Newtonian mechanics to apply them to a multi-parameter mechanical system in a few hours/days is ~0. Any theory of mechanics developed from scratch in such a short period will be terrible and fail to generalize as soon as the system changes a little bit.
But what about solving a simpler problem? Something non-trivial but purely geometric or symbolic or something for which a complete theory could realistically be developed by a group of people passing down data and speculation through several rounds of tests. Is it still true that the blind optimizers outperform the theorizers?
What I'm getting at is that this study seems to point to a really interesting and useful limitation to "amateur" theorizing, but if the system under study is sufficiently complicated, it becomes easy to explain the results with the less interesting, less useful claim that a group of non-specialists will not, in a matter of hours or days, come up with a theory that required a community of specialists years to come up with.
For instance, a bunch of undergrads in a psych study are not going to rederive general relativity to improve the chances of predicting when pictures of stars look distorted - clearly in that case the random optimizers will do better but this tells us little about the expected success of amateur theorizing in less ridiculously complicated domains.