The real bullet that is bitten to avoid induction is in step 1 (which is almost always a false dilemma). I see lots of other commenters see this too.
I don't see how this is any different from, say, Bayesian inference. Ultimately your inferences depend on the model being true. You might add a bunch of complications to the model in order to take into account many possibilities so that this is less of a problem, but ultimately your inferences are going to rely on what the model says and if your model isn't (approximately) true, well you're in trouble whether or not you're doing Bayesian inference or NHST or anything else.
(Though I suppose you could bite the bullet and say "you're right, Bayes' isn't attempting to do induction either." That would honestly surprise me.)
Edit: This is to say that I think you (and others) have a good argument for building better models - and maybe NHST practitioners are particularly bad about this - but I'm not talking about any specific model or the details of what NHST practitioners actually do. I'm talking about the general idea of hypothesis testing.
Just to make sure we are using the same terminology, what do you mean by "model" (statistical model e.g. set of densities?) and "induction"?
By model I do mean a statistical model. I'm not being terribly precise with the term "induction" but I mean something like "drawing conclusions from observation or data."
Ok. If a Bayesian picks among a set of models, then it is true that (s)he assumes the disjunctive model is true.. (that is the set of densities that came from either H0 or H1 or H2 or ...) but I suppose any procedure for "drawing conclusions from data" must assume something like that.
I don't think there is a substantial difference between how Bayesians and frequentists deal with induction, so in that sense I am biting the bullet you mention. The real difference is frequentists make universally quantified statements, and Bayesians make statements about functions of the posterior.
- Either the null hypothesis or the alternative hypothesis is true.
Nope. This was a good point by Jaynes. The truth may not exist in your hypothesis space. It may be (and often is) something you haven't conceived of.
\4. Therefore under the null hypothesis, our sample is extremely unlikely.
\5. Therefore the null hypothesis is false.
Low likelihood of data under a hypothesis in no way implies rejection of that hypothesis.
\6. Therefore the alternative hypothesis is true.
Without also calculating the likelihood under the alternative hypothesis (it may be less), this is unjustified as well.
Nope. This was a good point by Jaynes. The truth may not exist in your hypothesis space. It may be (and often is) something you haven't conceived of.
Yes, the implicit assumption here is that the model is true.
Low likelihood of data under a hypothesis in no way implies rejection of that hypothesis.
\6. Therefore the alternative hypothesis is true.
Without also calculating the likelihood under the alternative hypothesis (it may be less), this is unjustified as well.
I don't think you understood my point. I'm avoiding claiming any inductive theory is correct - including Bayes' - and trying to show how hypothesis testing may be a way to do induction while simultaneously being agnostic about the correct theory. That Bayesian theory rejects certain steps of the hypothesis testing process is irrelevant to my point (and if you read closely, you'll see that I acknowledge it anyway).
Yes, the implicit assumption here is that the model is true.
I think that's a bad assumption, and if you're trying to steelman, you should avoid relying on bad assumptions.
I'm avoiding claiming any inductive theory is correct
Going from 4 to 5 looks dependent on an inductive theory to me.
I think that's a bad assumption, and if you're trying to steelman, you should avoid relying on bad assumptions.
In any given problem the model is almost certainly false, but whether you use frequentist or Bayesian inference you have to implicitly assume that it's (approximately) true in order to actually conduct inference. Saying "don't assume the model is true because it isn't" is unhelpful and a nonstarter. If you actually want to get an answer, you have to assume something even if you know it isn't quite right.
Going from 4 to 5 looks dependent on an inductive theory to me.
Why yes it does. Did you read what I wrote about that?
Saying "don't assume the model is true because it isn't" is unhelpful and a nonstarter.
It starts fine for me.
Testing just the Null hypothesis is the least one can do. Then one can test the alternative, That way you at least get a likelihood ratio. You can add priors or not. Then one can build in terms modeling your ignorance.
See previous comment: http://lesswrong.com/lw/gqt/the_logic_of_the_hypothesis_test_a_steel_man/8ioc
One could keep going and going on modeling ignorance, but few even get that far, and I suspect it isn't helpful to go further.
Why yes it does. Did you read what I wrote about that?
Yes. It conflicted with what you subsequently wrote:
I'm avoiding claiming any inductive theory is correct
Testing just the Null hypothesis is the least one can do. Then one can test the alternative, That way you at least get a likelihood ratio. You can add priors or not. Then one can build in terms modeling your ignorance.
This doesn't address the problem that the truth isn't in your hypothesis space (which is what I thought you were criticizing me for). If your model assumes constant variance, for example, when in truth there's nonconstant variance, the truth is outside your hypothesis space. You're not even considering it as a possibility. What does considering likelihood ratios of the hypotheses in your hypothesis space do to help you out here?
See previous comment: http://lesswrong.com/lw/gqt/the_logic_of_the_hypothesis_test_a_steel_man/8ioc
Reading that thread, I think jsteinart is right - if the truth is outside of your hypothesis space, you're screwed no matter if you're a Bayesian or a frequentist (which is a much more succinct way of putting my response to you). Setting up a "everything else" hypothesis doesn't really help because you can't compute a likelihood without some assumptions that, in all probability, expose you to the problem you're trying to avoid.
Yes. It conflicted with what you subsequently wrote:
Are you happier if I say that Bayes is a "thick" inductive theory and that NHST can be viewed as induction with a "thin" theory which therefore keeps you from committing yourself to as much? (I do acknowledge that others treat NHST as a "thick" theory and that this difference seems like it should result in differences in the details of actually doing hypothesis tests.)
What does considering likelihood ratios of the hypotheses in your hypothesis space do to help you out here?
The likelihood ratio was for comparing the hypotheses under consideration, the Null and the alternative. My point is that the likelihood of the alternative isn't taken into consideration at all. Prior to anything Bayesian, hypothesis testing moved from only modeling the likelihood of the null to also modeling the likelihood of a specified alternative, and comparing the two.
if the truth is outside of your hypothesis space, you're screwed no matter if you're a Bayesian or a frequentist
Therefore, you put an error placeholder of appropriate magnitude onto "it's out of my hypothesis space" so that unreasonable results have some systematic check.
And the difference between Bayesian and NHST isn't primarily how many assumptions you've committed too, which is enormous, but how many of those assumptions you've identified, and how you've specified them.
Going from 4 to 5 seems to me like silently changing "if A then B" to "if B then A". Which is a logical mistake that many people do.
More precisely, it is a silent change from "if NULL, then DATA with very low proability" to "if DATA, then NULL with very low probability".
Specific example: Imagine a box containing 1 green circle, 10 red circles, and 100 red squares; you choose a random item. It is true that "if you choose a red item, it is unlikely to be a circle". But it is not true that "if you choose a circle, it is unlikely to be red".
Nope. This was a good point by Jaynes. The truth may not exist in your hypothesis space. It may be (and often is) something you haven't conceived of.
If the truth doesn't exist in your hypothesis space then Bayesian methods are just as screwed as frequentist methods. In fact, Bayesian methods can grow increasingly confident that an incorrect hypothesis is true in this case. I don't see how this is a weakness of Matt's argument.
The details are hazy at this point, but by assigning a realistic probability to the "Something else" hypothesis, you avoid making over confident estimates of your other hypotheses in a multiple hypothesis testing scenario.
See Multiple Hypothesis Testing in Jaynes PTTLOS, starting pg. 98, and the punchline on pg. 105:
In summary, the role of our new hypothesis C was only to be held in abeyace until needed, like a fire extinguisher. In a normal testing situation, it is "dead", playing no part in the inference because its probability remains far below that of the other hypotheses. But a dead hypothesis can be brought back to life by very unexpected data.
I think this is especially relevant to standard "null hypothesis" hypothesis testing because the likelihood of the data under the alternative hypothesis is never calculated, so you don't even get a hint that your model might just suck, and instead conclude that the null hypothesis should be rejected.
What is the likelihood of the "something else" hypothesis? I don't think this is really a general remedy.
Also, you can get the same thing in the hypothesis testing framework by doing two hypothesis tests, one of which is a comparison to the "something else" hypothesis and one of which is a comparison to the original null hypothesis.
Finally, while I forgot to mention this above, in most cases where hypothesis testing is applied, you actually are considering all possibilities, because you are doing something like P0 = "X <= 0", P1 = "X > 0" and these really are logically the only possibilities =) [although I guess often you need to make some assumptions on the probabilistic dependencies among your samples to get good bounds].
Yes, you can say it in that framework. And you should. That's part of the steelmanning exercise - putting in the things that are missing. If you steelman enough, you get to be a good bayesian.
P0 = "X <= 0" and {All My other assumptions}
NOT(P0) = NOT("X <= 0") or NOT({All My other assumptions})
As a Bayesian, I'm very happy to see an attempted steelman of hypothesis testing. Too often I see Bayesian criticism of "frequentist" reasoning no frequentist statistician would ever actually apply. Unfortunately, this is a failed steelman (even granting the first premise) -- the description of the process of hypothesis testing is wrong, and as a result the the actual near-syllogism underlying hypothesis testing is not properly explained.
The first flaw with the description of the process is that it omits the need for some kind of ordering on the set of hypotheses, plus the need for a statistic -- a function of from the sample space to a totally ordered set -- such that more extreme statistic values are more probable (in some sense, e.g., ordered by median or ordered by expected value) the further an alternative is from the null. This is not too restrictive as a mathematical condition, but it often involves throwing away relevant information in the data (basically, any time there isn't a sufficient statistic).
The second flaw is that the third and fourth step of the syllogism should read something like "Under the null distribution, a statistic value as or more extreme than ours is extremely unlikely". Being able to say this is the point of the orderings discussed in the previous paragraph. Without the orderings, you're left talking about unlikely samples, which, as gjm pointed out, is not enough on its own to make the move from 4 to 5 even roughly truth-preserving. For example, that move would authorize the rejection of the null hypothesis "no miracle occurred" on these data.
As to the actual reasoning underlying the hypothesis testing procedure, it's helpful to think about the kinds of tests students are given in school. An idealized (i.e., impractical) test would deeply probe a student's understanding of the course material, such that a passing grade would be (in logical terms) both a necessary and a sufficient signifier of an adequate understanding of the material. In practice, it's only feasible to test a patchwork subset of the course material, which introduces an element of chance. A student whose understanding is just barely inadequate (by some arbitrary standard) might get lucky and be tested mostly on material she understands; and vice versa. The further the student's understanding lies from the threshold of bare adequacy, the less likely the test is to pass or fail in error.
In a closely analogous fashion, a hypothesis test is a probe for a certain kind of inadequacy in the statistical model. The statistic is the equivalent of the grade, and the threshold of statistical significance is equivalent of the standard of bare adequacy. And just as the standard of bare adequacy in the above metaphor is notional and arbitrary, the threshold of the hypothesis test need not be set in advance -- with the realized value of the statistic in hand, one can consider the entire class of hypothesis tests ex post facto. The p-value is one way of capturing this kind of information. For more on this line of reasoning, see the work of Deborah Mayo.
Thanks for this comment. I was attempting to abstract away from the specific details of NHST and talk about the general idea since in many particulars there is much to criticize, but it appears that I abstracted too much - the ordering of the hypothesis space (i.e. a monotone likelihood ratio as in Neyman-Pearson) is definitely necessary.
In a closely analogous fashion, a hypothesis test is a probe for a certain kind of inadequacy in the statistical model. The statistic is the equivalent of the grade, and the threshold of statistical significance is equivalent of the standard of bare adequacy.
This seems to back up my claim that we can still view NHST as a sort of induction without a detailed theory of induction (though the reasons for and nature of this "thin" induction must be different from what I was thinking about). Do you agree?
I agree that the quote seems to back up the claim, but I don't agree with the claim. Like all frequentist procedures, NHST does have a detailed theory of induction founded on the notion that one can use just the (model's) sampling probability of a realized event to generate well-warranted claims about some hypothesis/hypotheses. (Again, see the work of Deborah Mayo.)
My understanding of standardised hypothesis tests was that they serve the purposes of
There are practical reasons for both purposes. (1) is useful because the alternative hypothesis is usually more complex than the null and can have lots of parameters, thus calculating probabilities under the alternative may become impossible, especially with limited computing power. As for (2), science is a social institution - journal editors need a tool to reject publishing unfounded hypotheses without risk of being accused of having "unfair" priors, or whatever.
However I don't understand how exactly hypothesis tests help to solve the philosophical problems with induction. Perhaps it would be helpful to list several different popular philosophical approaches to induction (not sure what are the major competing paradigms here - perhaps Bayesianism, falsificationism, "induction is impossible"?), present example of problems where the proponents of particular paradigms disagree about the conclusion, and show how a hypothesis test could resolve the disagreement?
However I don't understand how exactly hypothesis tests help to solve the philosophical problems with induction.
I don't think it does, in fact I'm not claiming that in my post. I'm trying to set up hypothesis testing as a way of doing induction without trying to solve the problem of induction.
I don't think hypothesis testing would resolve disagreements among competing paradigms either - well maybe it could, but I'm not talking about that.
(I think you're largely correct about why, in actual fact, hypothesis testing is used. There's also some element of inertia as well)
a way of doing induction without trying to solve the problem of induction
Well, this is the thing I have problems to understand. The problem of induction is a "problem" due to the existence of incompatible philosophical approaches; there is no "problem of deduction" to solve because everybody agrees how to do that (mostly). Doing induction without solving the problem would be possible if people agreed how to do it and the disagreement was confined to inconsequential philosophical interpretations of the process. Then it would indeed be wise to do the practical stuff and ignore the philosophy.
But this is probably not the case; people seem to disagree about how to do the induction, and there are people (well represented on this site) who have reservations against frequentist hypothesis testing. I am confused.
I think Matt's point is that under essentially all seriously proposed versions of induction currently in existence, the technique he described constitutes a valid inductive inference, therefore, in at least the cases where hypothesis testing works, we don't have to worry about resolving the different approaches.
You're right - we have to have some idea of how to do induction in order to do it without fully fleshing out the details, but the unresolved issues don't have to be confined to inconsequential philosophical interpretations. For example, we could just avoid doing induction except for when what seem like plausible approaches agree. (This is probably a better approach to "robust induction" than I proposed in my post).
I think a steel man for hypothesis testing should be focused on the types of problems that it can solve better than Bayesian methods can. After all, that's what the purpose of these tests is.
I hope you informed them about the fact that real people often don't satisfy condition (1). Instead they write things like "The patients in the treatment group showed dramatically decreased risk of stroke (p<0.01), indicating the efficacy of Progenitorivox."
it does seem to be a useful steel man.
Find a steel man in there somewhere, and then we can talk about the properties of said steel man.
But it isn't theory-of-induction-free. It just pretends to be. There's a theory of induction right in there, where you correctly identify it, in step 4->5. It's no better, no more likely to be true, and no more robust, merely on account of being squashed up small and hidden.
You haven't truly minimized the "amount of induction" in the argument; only the "amount of induction that's easily visible", which I don't think is a parameter that deserves minimizing. You'd need just the same amount of induction if, say, instead of doing classical NHST you did Bayesian inference or maximum likelihood (= Bayesian inference where you pretend not to have priors) or something. You could squash it up just as small, too; you'd just need to make steps 1-4 more quantitative.
Consider a case -- they're not hard to find -- where you have a test statistic that's low-probability on any of your model hypotheses. Then the same logic as you've used says that you're "forced" to conclude that all your hypotheses are false -- even if it happens that one of them is right. (In practice your model is never exactly right, but never mind that.) To me, this shows that the whole enterprise is fundamentally non-deductive, and that trying to make it look as much as possible like a pure deduction is actively harmful.
Maybe a better way of phrasing what I'm trying to point out is that induction is isolated to a single step. Instead of working directly with probabilities which require a theory of what probabilities are, NHST waves it's hands a bit and treats the inductive step as deductive, but transparently so (once you lay out the deduction anyway).
Your point about a test statistic that's low-probability on all possible model hypotheses is a good one - and it suggests that the details of hypothesis testing should change even if the general logic is kept. I doubt that the details of actually used hypothesis testing are ideal for "induction-free induction" (which I'm realizing is a bad name for what I'm trying to convey), but what I'm really talking about is the general logic. I'd be surprised if some of the details didn't have to change.
I don't think I disagree with anything in your comment though. I don't think I have a strong argument for using hypothesis testing, but it may be that the general logic can be salvaged for a reasonable method of doing induction without fully fleshing out an inductive theory (this is why I said one step requires hand waving).
What's interesting to me about this process is that it almost tries to avoid induction altogether. Only the move from step 4 to 5 seems anything like an inductive argument. The rest is purely deductive - though admittedly it takes a couple premises in order to quantify just how likely our sample was and that surely has something to do with induction. But it's still a bit like solving the problem of induction by sweeping it under the rug then putting a big heavy deduction table on top so no one notices the lumps underneath.
One interesting thing here is that you start with a null vs other hypothesis, but that's because you're doing a two-sample z/t-test. But what's going on when you do a one sample z/t-test and get out a confidence interval?
The one sided hypothesis test is still null vs. other because it uses the full parameter space, i.e. it's H0: mu <= c vs. Ha: mu > c. We present it to undergrads as H0: mu = c vs. Ha: mu > c in order to simplify (I think that's the reason anyway) but really we're testing the former. The Karlin-Rubin theorem justifies this.
I don't follow... that sounds like you're giving the definition of a one-tailed hypothesis test. What does that have to do with a constant c? Suppose I do this in R:
R> set.seed(12345); t.test(rnorm(20))
One Sample t-test
data: rnorm(20)
t = 0.4103, df = 19, p-value = 0.6861
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.3138 0.4668
sample estimates:
mean of x
0.07652
And get a 95% CI of (-0.3138-0.4668); if my null hypothesis (H0) is my mu or sample mean (0.07652), then you say my Ha is mu > c, or 0.07652 > c. What is this c?
So rereading your first comment, I realize you said one-sample vs. two-sample hypothesis test and not one-sided vs. two-sided (ore one-tailed vs. two-tailed). If that's what you meant, I don't follow your first comment. The t-test I gave in the post is a one-sample test - and I don't understand how the difference between the two is relevant here.
But to answer your question anyway:
I don't follow... that sounds like you're giving the definition of a one-tailed hypothesis test. What does that have to do with a constant c? Suppose I do this in R:
And get a 95% CI of (-0.3138-0.4668); if my null hypothesis (H0) is my mu or sample mean (0.07652), then you say my Ha is mu > c, or 0.07652 > c. What is this c?
c is the value you're testing as the null hypothesis. In that R-code, R assumes that c=0 so that H0: mu=c and Ha: mu=/=c. For the R code:
t.test(data, alternative="greater", mu=c)
You perform a t test with H0: mu<=c and Ha: mu>c.
I'm interested in the calculated confidence interval, not the p-value necessarily. Noodling around some more, I think I'm starting to understand it more: the confidence interval isn't calculated with respect to the H0 of 0 which the R code defaults to, it's calculated based purely on the mean (and then an H0 of 0 is assumed to spit out some p-value)
R> set.seed(12345); t.test(rnorm(20,100,15))
One Sample t-test
data: rnorm(20, 100, 15)
t = 36.16, df = 19, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
95.29 107.00
sample estimates:
mean of x
101.1
R>
R> 107-95.29
[1] 11.71
R> 107 - (11.71/2)
[1] 101.1
Hm... I'm trying to fit this assumption into your framework....
A 95% confidence interval is sort of like testing H0:mu=c vs Ha:mu=\=c for all values of c at the same time. In fact if you reject the null hypothesis for a given c when c is outside your calculated confidence interval and fail to reject otherwise, you're performing the exact same t-test with the exact same rejection criteria as the usual one (that is if the p-value is less than 0.05).
The formula for the test statistic is (generally) t = (estimate - c)/(standard error of estimate) while the formula for a confidence interval is (generally) estimate +/- t^(standard error of estimate) where t^ is a quantile of the t distribution with appropriate degrees of freedom, chosen according to your desired confidence level. t^* and the threshold for rejecting the null in a hypothesis test are intimately related. If you google "confidence intervals and p values" I'm sure you'll find a more polished and detailed explanation of this than mine.
Related to: Beyond Bayesians and Frequentists
Update: This comment by Cyan clearly explains the mistake I made - I forgot that the ordering of the hypothesis space is important is necessary for hypothesis testing to work. I'm not entirely convinced that NHST can't be recast in some "thin" theory of induction that may well change the details of the actual test, but I have no idea how to formalize this notion of a "thin" theory and most of the commenters either 1) misunderstood my aim (my fault, not theirs) or 2) don't think it can be formalized.
I'm teaching an econometrics course this semester and one of the things I'm trying to do is make sure that my students actually understand the logic of the hypothesis test. You can motivate it in terms of controlling false positives but that sort of interpretation doesn't seem to be generally applicable. Another motivation is a simple deductive syllogism with a small but very important inductive component. I'm borrowing the idea from a something we discussed in a course I had with Mark Kaiser - he called it the "nested syllogism of experimentation." I think it applies equally well to most or even all hypothesis tests. It goes something like this:
1. Either the null hypothesis or the alternative hypothesis is true.
2. If the null hypothesis is true, then the data has a certain probability distribution.
3. Under this distribution, our sample is extremely unlikely.
4. Therefore under the null hypothesis, our sample is extremely unlikely.
5. Therefore the null hypothesis is false.
6. Therefore the alternative hypothesis is true.
An example looks like this:
Suppose we have a random sample from a population with a normal distribution that has an unknown mean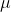 and unknown variance
and unknown variance 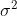 . Then:
. Then:
1. Either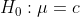 or
or 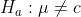 where
where  is some constant.
is some constant.
2. Construct the test statistic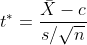 where
where  is the sample size,
is the sample size, 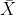 is the sample mean, and
is the sample mean, and  is the sample standard deviation.
is the sample standard deviation.
3. Under the null hypothesis,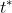 has a
has a 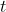 distribution with
distribution with  degrees of freedom.
degrees of freedom.
4.) is really small under the null hypothesis (e.g. less than 0.05).
is really small under the null hypothesis (e.g. less than 0.05).
5. Therefore the null hypothesis is false.
6. Therefore the alternative hypothesis is true.
What's interesting to me about this process is that it almost tries to avoid induction altogether. Only the move from step 4 to 5 seems anything like an inductive argument. The rest is purely deductive - though admittedly it takes a couple premises in order to quantify just how likely our sample was and that surely has something to do with induction. But it's still a bit like solving the problem of induction by sweeping it under the rug then putting a big heavy deduction table on top so no one notices the lumps underneath.
This sounds like it's a criticism, but actually I think it might be a virtue to minimize the amount of induction in your argument. Suppose you're really uncertain about how to handle induction. Maybe you see a lot of plausible sounding approaches, but you can poke holes in all of them. So instead of trying to actually solve the problem of induction, you set out to come up with a process which is robust to alternative views of induction. Ideally, if one or another theory of induction turns out to be correct, you'd like it to do the least damage possible to any specific inductive inferences you've made. One way to do this is to avoid induction as much as possible so that you prevent "inductive contamination" spreading to everything you believe.
That's exactly what hypothesis testing seems to do. You start with a set of premises and keep deriving logical conclusions from them until you're forced to say "this seems really unlikely if a certain hypothesis is true, so we'll assume that the hypothesis is false" in order to get any further. Then you just keep on deriving logical conclusions with your new premise. Bayesians start yelling about the base rate fallacy in the inductive step, but they're presupposing their own theory of induction. If you're trying to be robust to inductive theories, why should you listen to a Bayesian instead of anyone else?
Now does hypothesis testing actually accomplish induction that is robust to philosophical views of induction? Well, I don't know - I'm really just spitballing here. But it does seem to be a useful steel man.