Yes, I undestand that the crude model glimpsed is more related to the naivest many-worlds bifurcation than the full neo-everettian framework, and it surely is not the first time that I've intuited a connection that, when mathematic rubber met the road, turned out to be an error. I will stick to logic of course, since it's a logic enterprise, but I still suspect there will be applicable models to physics. Time and dedicated effort will tell!
I thought you were going to talk about mathematics, but you seem to start out talking about mathematics and then go on to make a lot of either meaningless or unjustified claims about reality on the basis of some exciting-sounding words you used in the mathematics. It's unclear to me what you're actually talking about and why.
As I read this, "Synaptic Pruning!!!!!!!" keeps leaping into my brain, complete with exclamation points.
I don't have much useful to say on the subject, though, since I only having a passing knowledge of either, it just seems like the two are related.
Might be a subset of the phoenomenon: if you can relate truth to connectedness, triviality to maximal connectedness and falsifying a sentence with pruning connections, you could have a workable model. Interesting avenue, though.
Will add to the program!
The very big problem with this proposition is that as soon as you take all propositions to be true, you have no method for determining the falsity of any propositions. From any contradictorily accepted propositions any statement can be determined true.
To make this work, you would have to start with a small set of unprovable axiomatic negations, and then build from there. In other words, there is no essential difference between "destructive mathematics" and constructive mathematics, and destructive mathematics has to take a useless rigamarole around the concept of truth and falsity and rebuild constructive mathematics. All statements cannot be assumed to be true or false, they are indeterminate. Formal logic takes axioms and derives what is determinably true and false from those parameters.
I'm sorry, but this concept is useless.
From any contradictorily accepted propositions any statement can be determined true.
This is true in classical logic, but not in paraconsistent logic systems. They can prove fewer propositions than classical logic, but there are some situations in which you might want to use one.
I still don't see a point in assuming every statement to be true. It seems more like a gimmick than anything else. Even without the principle of explosion, there must be a distinction between what is proved to be not false and what isn't. What use is there in assuming everything to be true?
I see no point in this theory. The application to MWI doesn't really make sense, and even if it did, that's no reason to give this proposition any credence. The Tegmark hypothesis is also misunderstood; it states that all well-formed mathematical structures complex enough to have self-aware systems subjectively exist to those systems. I am not sure this can be proven, but I see even less of a connection to "destructive mathematics" than MWI.
How is this useful to logic?
Follow-up to: Constructive mathematics and its dual
In last post, I've introduced constructive mathmatics, intuitionistic logic (JL) and its dual, uninspiringly called dual-intuitionistic logic (DL).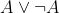 is no more a tautology (although it can still be true for some formula, precisely for those that already have a proof or a refutation).
is no more a tautology (although it can still be true for some formula, precisely for those that already have a proof or a refutation).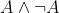 is still always false, and so JL incorporates
is still always false, and so JL incorporates ) , a principle called the law of non-contradiction.
, a principle called the law of non-contradiction.
I've said that JL differs from classical logic about the status of the law of excluded middle, a principle valid in the latter which states that a formula can be meaningfully only asserted or negated. This, in the meta-theory, means you can prove that something is true if you can show that its negation is false.
Constructivists, coming from a philosophical platform that regards mathematics as a construction of the human mind, refuse this principle: their idea is that a formula can be said to be true if and only if there is a direct proof of it. Similarly, a formula can be said to be false if and only if there's a direct proof of its negation. If no proof or refutation exists yet (as is the case today, for example, for the Goldbach conjecture), then nothing can be said about A.
Thus
Intuitionism anyway (the most prominent subset of the constructivist program), thinks that
Intuitionistic logic has no built-in model of time, but you can picture the mental activity of an adherent in this way: he starts with no (or very little) truths, and incorporates in his theory only those theorems of which he can build a proof of, and the negation of those theorems that he can produce a refutation of.
Mathematics, as an endeavour, is seen as an accumulation of truth from an empty base.
I've also indicated that there's a direct dual of JL, which is part of a wider class of systems collecively known as paraconsistent logics. Compared to the amount of studies dedicate to intuitionistic logic, DL is basically unknown, but you can consult for example this paper and this one.
In this second article, a model is presented for which DL is valid, and we can read the following quote: "[These semantics] reflect the notion that our current knowledge about the falsity of statements can increase. Some statements whose falsity status was previously indeterminate can down the track be established as false. The value false corresponds to firmly established falsity that is preserved with the advancement of knowledge whilst the value true corresponds to 'not false yet'".
My suggestion is to be a lot braver in our epistemology: let's suppose that the natural cognitive state is not one of utter ignorance, but of triviality. Let's then just assume that in the beginning, everything is true.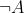 will expunge A from the set of truth, the refutation of A will remove
will expunge A from the set of truth, the refutation of A will remove 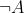 .
.
Our job then, as mathematician, is to discover refutations: the refutation of
This dual of constructive mathematics just begs to be called destructive mathematics (or destructivism): as a program, it means to start with the maximal possibility and to develop careful collection of falsities.
Be careful though: it doesn't necessarily mean that we accept the existence of actual contradictions. It might be very well the case that in our world (or model of interest) there are no contradictions, we 'just' need to expunge the relevant assertions.
As the dual of constructive mathematics, destructivism regards mathematics as a mental construction, one though that procedes from triviality through confutations.
One major difficulty with destructive mathematics is that, to arrive to a finite set of truths, you need to destroy an infinite amount of falsities (but, on the other side, to arrive to a finite set of falsities in constructive mathematics you need to assert an infinite number of truths).
Usually, we are more interested in truth, so why should we embark in such an effort?
I can see at least two weak and two strong reasons, plus another one that counts as entertainment of which I'll talk about more extensively in the last post.
The first weak reason is that sometimes, we are more interested in falsity rather than truth. Destructivism seems to be a more natural background for the calculus of resolution, although, to my knowledge, this has only been developed in classical setting.
The second weak reason is that destructivism is an interesting choice for coalgebraic methods in computer science: there, co-induction and co-recursion are a method for 'observing' or 'destroying' (potentially) infinite objects. From the Wikipedia entry on coinduction: "As a definition or specification, coinduction describes how an object may be "observed", "broken down" or "destructed" into simpler objects. As a proof technique, it may be used to show that an equation is satisfied by all possible implementations of such a specification."
I whish I could say more, but I don't know much myself: the parallelisms are tempting, but I have to leave the discovery of eventual low-hanging fruits to later times or someone else entirely.
Two instead much more promising fields of application are Tegmark universes and the Many World quantum mechanics.
It's difficult to give a cogent account for why all the mathematical structures should exists, but Tegmark position equates simply a platonist point of view on destructivism.
If all formulas are true, then this means that "somewhere" every model is realized, while on the other side, if all structures are realized, then "on the whole", every formula is true (somewhere).
But the most important reason why one should adopt this framework is that it gives a natural account of quantum mechanics in the Many World flavour (MWI).
Usually, physical laws are seeen as the corrispondence between physically realizable states, and time is the "adjunction" of new states from older ones. Do you recognize anything?
What if, instead, physical laws dictates only those states that ought to be excluded and time is simply the 'destruction' or 'localization' of all those possible states? Well, then you have (almost for free) MWI: every state is realized, but in times you are constrained to just one.
I'm extremely tempted to say that MWI is the dual of the wave function collapse, but of course I cannot (yet) prove it. Or should I just say that I cannot yet disprove it's not like that?
If that's the case, the mystery of why subjective probability follows the Born rule will be 'just' the dual of the non-linear mechanism of collapse. One mystery for a mystery.
I also suspect that destructive mathematics might have implication even for probability theory, but... This framework is still in its infancy, so who knows?
The last interesting motivation for taking seriously destructive mathematics is that it offers a possible coherent account of Chtulhu mythos (!!): what if God, instead of having created only this world from nothing out of pure love, has destructed every world but this one out of pure hate? If you accept the first scenario, then the second scenario is equally plausible / conceivable. I'll explore the theme in the last post: Azathoth hates us all!