Ouch, don't the units in that diagram hurt your brain? (Yeah, I understand what it means and it does make sense, but it looks soooo wrong. Especially in my part of the world where an ounce is a unit of mass or weight, not of volume.)
I think you can use this logic to explain why movie theaters sell small, medium, large, and extra large popcorn for $5, $6, $7, and $8 respectively. With the less attractive options priced relatively high, people are more likely to pay the unreasonable price of $8 for the extra large.
Hmmm...
29/36 $2.00 = $1.61 7/36 $9.00 = $1.75
While the average prices (equivalence values) placed on these options were $1.25 and $2.11 respectively
I guess people don't carry calculators with them?
All psychologically normal people carry a calculator between their ears. Most are just too lazy to use theirs, even for easy problems like this, which is the source of many biases.
I'd say embarrassment is a bigger issue than laziness. People don't want to be seen as nerdy, especially about little things. Also, if some people are slow at mental math, they wouldn't want others to know that.
I am interested in this phenomenon as I have run afoul of it many times. I will describe what I have experienced in the role of the person doing the unwanted calculations. Let's suppose that people have made what appears to me to be a "guess choice", and I do the math and realize that another choice makes more sense optimizing for the thing they are representing themselves to be optimizing for. I point this out, and it is rejected. Here are some reasons I have perceived.
But most commonly (in my observation), and most importantly (to me)!
The math is easy if you just ignore the /36 which is the same in both casts. 2*29=58 and 7*9 = 63. No calculator required.
I bought my brother a huge gold buttplug for $250 (top of the line) rather than a medium range coat from The North Face.
"Naturally, those so-called "lotteries" were a failure. They had no moral force whatsoever; they appealed not to all a man's faculties, but only to his hopefulness. Public indifference soon meant that the merchants who had founded these venal lotteries began to lose money. Someone tried something new: including among the list of lucky numbers a few unlucky draws. This innovation meant that those who bought those numbered rectangles now had a twofold chance: they might win a sum of money or they might be required to pay a fine--sometimes a considerable one. As one might expect, that small risk (for every thirty "good" numbers there was one ill-omened one) piqued the public's interest. Babylonians flocked to buy tickets."
-Jorge Luis Borges, The Lottery in Babylon.
Long ago I was discussing this passage with a friend trained in economics (I am not). He insisted that is was silly and that people would never prefer deliberately the option with added penalties for losing. Glad to see he was wrong!
Why would that make you glad? You found out your prediction was correct, which is good, but you also found out people are idiots, which is very bad.
I know I might feel glad because I feel like I have a lot more control over whether I am right or wrong than the relative idiocy of the average person. On the other hand, being a person, I'd probably just be glad either way. The upside of being cynical.
When buying $10 dust specks, do not get carried away and buy 3^^^3 of them. You won't save any money that way.
It's a ludicrously large number in Knuth's up-arrow notation used in some posts as an example of a number which is finite, but large enough to ludicrously surpass reasonable finite numbers like the size of the universe, or the number of possible states of a volume the size of the Solar System, or whatever.
But why is "3" chosen rather than another single-digit integer? I can see why 0 or 1 would not be chosen, obviously, and 2 could confuse people by appearing non-arbitrary due to the role of binary in computer science. Is 3 simply the first viable positive integer that came along?
But don't forget the main lesson of the economics of present giving: "It's the thought that counts". If you can find a €40 item that seems personalised and full of meaning, it's valued much more than the €50 bottle of mindless perfume.
Of course, it's much easier to be considerate if you know the person well. The closer you are, the more you know their preferences, and the more they will value your consideration. So be cheap and attentive to those closest to you, moving up to spendthrift and indifferent for strangers...
(that actually is my pattern of spending - are others in the same boat?)
It's also possible to be hit by this bias if you're not thinking of it while shopping. Last year, I was invited over to watch the Super Bowl at a friend's, and they were also celebrating his niece's birthday. Of course, I brought a gift -- a Cookie Monster plushie. Unfortunately for me, someone else brought a teddy bear that was obviously much larger and higher quality! Oops.
The moral, I suppose, is that if you're going to get a cheaper gift, shoot for something that's very different than what other people are likely to buy.
This advice on Christmas gifts will only work if you leave the price tag on, or if your recipient is sophisticated enough to recognize, say, that a particular scarf is worth $45. I once opened a package that I received in a gift-swap game that contained a (to my eyes, rather ordinary) Christmas ornament. My face must not have shown the proper appreciation, as my wife then whispered to me that this was a very expensive ornament. Evidently the givers had instinctively followed the "expensive junk" philosophy but the effect was nearly lost on unsophisticated me.
Thanks for this over the holidays. (You asked for feedback from practical applications).
It helped me come to the realization on why some stores can get away with put horribly, stupidly expensive chocolates on display right at the counter top: not only do they want you to buy it (duh), but it also lets your recipients know that you bought them a $5.99 bar of chocolate that would otherwise be indistinguishable from the larger $1.49 chocolate bars at the grocery store (assuming that your recipients have shopped at the same stores as you and are aware of how "nice" the gift is).
As a result we bought several overpriced chocolate bars to show how generous we were.
Another good item which I bought for someone for his birthday (unconciously following the above advice) was a $15 version of the fifteen puzzle. Compare vs. an $18 paperback book I was considering for that gift.
Now I'm wrestling with the inverse problem. I find myself wanting an Asus Eee PC, and justifying it to my wife because of how cheap it is - $399. Which is the same price as the PS3, which I don't even bring up because of how expensive it is - $399.
I find myself doing this, and even consciously recognizing it often doesn't change my actions. For example, if a half-rack of BBQ ribs costs $12.99 and a full rack costs $18.99, I'll 'upgrade' to the full rack since it seems like a waste to pay so much for a half rack. But if the only option was a full rack for $18.99, I'd order something else because that's too expensive.
I'll do this if I think there's any chance of my wanting the product again, and I don't want to have to pay the "entry fee" twice.
PS: If you actually use this trick, I want to know what you bought.
When my boss's son was born, I gave him an expensive stuffed animal hand-made from recycled material. I didn't deliberately use the trick -- when I was making the purchase, I remembered that I had read something about gifts to buy to appear generous on OB, but I couldn't remember the details. I took the price off the tag, but if my boss or his wife thought to Google the artisan, they would be able to see roughly how much I payed.
"Which is more memorable, a $25 shirt or a $25 candle?" I asked my younger brother and he said the shirt.
Also the 'theory' will only work if that person knows the worth(cost) of the item Or I guess you could leave the tags on.
Everyone I know always deliberately cuts the price tags off or goes over them with a permanent marker. It is considered gauche to show off how much or how little you spent on someone's gift. In this case, it might make more sense to put emphasis on how expensive the gift itself appears to be.
Is there a market, then, for products on which the price tag cannot be removed, thereby allowing you to demonstrate how expensive it is? Books are an example: often the price is listed on the cover (of course, unfortunately this mainly happens for paperback books, which are cheap).
I suppose you could also go over the price tag with an insufficiently opaque permanent marker.
Is there a market, then, for products on which the price tag cannot be removed, thereby allowing you to demonstrate how expensive it is? Books are an example: often the price is listed on the cover (of course, unfortunately this mainly happens for paperback books, which are cheap).
Where I am, it is customary for book stores to put a sticker onto the price printed on the cover when you ask them to wrap the book in wrapping paper.
A shirt is going to be more memorable because people use shirts constantly. The candle is used at most once.
Most of the shirts I've received as gifts I haven't actually worn, because they don't portray the image I'd like to (they're durable signals). A candle, as a private consumable, is something that I might burn even if it's incongruent, because burning it doesn't represent a commitment. (This is a strong, potentially non-obvious reason to prefer consumables over durables when getting gifts for others.)
Beyond that, memorable isn't just "amount of time it's used" but "remarkability." I rarely think about my underwear; I just grab the top one out of the drawer, and I buy the cheapest variety above some quality threshold. I own one pair that's bright green that I bought for the lulz; even though I wear it about a twentieth of the time as the first variety, it's much more memorable because it stands out.
Of course- in large part because the target is smaller, and thus it signals much more precise knowledge about the recipient. If you don't have a strong ability to discern other people's preferences, go with expensive consumables, because that's a broader target and expectations are lower.
Isn't signalling knowledge about the recipient pretty much the whole point of giving presents? Otherwise we'd just give people cash.
You can signal various other things too like sophisticated taste or having spent time picking/creating the present etc.
Either it isn't, or many people do an incredibly poor job. There are even specific events for getting rid of flop gifts (white elephant parties) and a phrase for how to get rid of a poor gift (re-gifting).
When I am given a candle, which I can save for power outages or impromptu celebrations or even just give it to somebody else, I am glad because 1) I'm not likely to buy one for myself but every single time I see it in a shop I think I would, were it only slightly cheaper, 2) it is a focus point, a symbol of voluntary solitude, even a cheap one, and in this way very unlike a shirt (although I have a couple shirts which for me have symbolic significance), 3) I am a twin who likes having her own things even if I don't mind sharing, and I have loaned clothes when other people were in need, and candles when we all were.
So candles trump shirts on all counts!:))
I'm collecting quotes to help me remember all the things that I should be remembering in order to overcome bias, and I'm wondering if someone has one for the sub-sequence on the Affect Heuristic.
and your goal is to display your friendship, rather than to actually help the recipient
I don't think that appearing to have spent a lot is the best way to achieve that, even if you manipulate what amount of money they think of as a lot. You'd better give some imaginative present that suits the recipient's tastes well. (Making something yourself rather than buying it is even better.)
PS: If you actually use this trick, I want to know what you bought.
I have a sister who is very sensitive to her financial situation and will refuse to accept most gifts I've offered. She allowed that I might bring a salad to her recent birthday party - so I brought one of the cheaper ones from Edible Arrangements. She loved it, and I was able to spend about my price range on a gift for her.
Gosh, it's amazing the biases we have when the data is non-evaluatable, and then even when we can compare, we still have a bias towards an overflowing but smaller can, and an under filled but bigger can. The funny thing is I realize I've thought this way, too, until I read this just now. I shall not make the mistake again!
I shall not make the mistake again!
You probably will. I think this biases thing doesn't disappear even when you're aware of it. It's a generic human feature. I think self-critical awareness will always slip at the crucial moment; it's important to remember this and acknowledge it. Big things vs small things as it were.
. I think self-critical awareness will always slip at the crucial moment
The point is to be lesswrong! :)
I'm just a regular guy who stumbled on LessWrong some time ago, and it has helped me see a lot that I was missing in this world and, yes, to change my mind. Much of this stuff is hard to grasp for a man with limited math skills, but I think I may have an innate grasp of heuristics in some cases. At any rate, I have long made it a practice to budget an amount for a particular gift, and then seek out the smallest, most precious object that that amount will buy, rather than the biggest and most bountiful. (Except for children under 7 or so years of age--for them a big box trumps a small box no matter what's inside.) And I am not fooled by marketing tricks as often as my peers seem to be. Thank you all (commenters too!) for this great body of information. I intend to read every word in the whole wiki.
High-end brand neck tie or a scarf would be a classic example of this. You can also exploit the scarcity bias in this context. Find an antique item (e.g. something costs less than 50$ necktie) and tell that it's very rare and you spent some time to find it. In addition, they can never guess the price, it's an antique it can be hundreds of dollars who knows?
Are the gambling guys actually suggested that they will play several times? Because I, seeing both things side by side, still prefer 29/36 over 7/36 by the easy reasoning "better win $2 then nothing", and, if I'm only playing once, I claim it *is* a good strategy (otherwise you could play a lottery suggesting to win a billion with chances of 1 to million instead of working on a one-time job for $500 guaranteed - again, I claim it is salient to choose the job).
Because I, seeing both things side by side, still prefer 29/36 over 7/36 by the easy reasoning "better win $2 then nothing", and, if I'm only playing once, I claim it is a good strategy
You are not only playing once. If you follow a consistent decision making strategy, your choice should hold every time you face similar odds in the future. Or at least, for as long as you plan to play similar games.
Mathematically, $2 is the same as 50% chance to win $4, is the same as 25% chance to win $8. So every time I am offered $2 or 25% chance to win $9, I should choose the latter. (Most people however are extremely risk adversive - I think the ratio is something like 2:1, which leads to missed opportunities).
This holds for me, until someone offers me a million dollars or 50% chance to win whatever. I can retire on a million, everything above that is imaginary. Or until I am stranded in the mall with no wallet and desperately need $1.50 for a bus ticket. Which is why every investor needs 6 months worth of expenses - you don't want to close positions at a bad time, just so you can pay rent.
With that in mind - and if $9 still seems low - at what price would you choose the second bet?
One should factor in the odds of similar games occurring multiple times throughout one's life (unless one is a frequent visitor of casinos). I claim that *these* are too low for the situation to "add up to normality".
Answering the question asked... I could start *considering* the second choice at 25% chance of 15 (probably properly 16 but my gut feeling has, of course, rounded it) and preferring it at... well, maybe never?
One should factor in the odds of similar games occurring multiple times throughout one's life (unless one is a frequent visitor of casinos). I claim that these are too low for the situation to "add up to normality".
No, one shouldn't. Playing a game of chance once or a thousand times does not influence the outcome of the next round (aka the gambler's fallacy). If a bet is a good idea one time, it's a good idea a thousand times. And if a bet is a good idea a thousand times, it is a good idea the first time. How could you consider betting a thousand times to be a good idea, if you think each individual bet is a bad idea?
Besides that, even if you don't encounter exactly the same odds, you will encounter some odds. The numbers change, the way we make decisions remains the same.
The point of probabilities is not that the expected outcome occurs every time. The point is that it IS the expected outcome. You might never be asked to participate in a betting game at the Mall. But at the end of your life, the sum of all your bets, big and small, will (probably) add up to normality.
Answering the question asked... I could start considering the second choice at 25% chance of 15 (probably properly 16 but my gut feeling has, of course, rounded it) and preferring it at... well, maybe never?
So, to summarize (and simplify a bit) - you would start considering letting go of (almost) certain $2 only after the expected utility is (around) $4.
I am sure you will not be surprised to learn you are not atypical in your preference: "Some studies have suggested that losses are twice as powerful, psychologically, as gains.[1]" (https://en.m.wikipedia.org/wiki/Loss_aversion). You might also be interested in the following articles: https://en.m.wikipedia.org/wiki/Risk_aversion and https://theintactone.com/2018/05/04/bf-u3-topic-5-loss-aversion-gamblers-fallacy/
Now, just because behaviour is common doesn't mean it's wrong. The loss aversion bias is called a bias, because it does lead to missed opportunities.
For example, a combination of loss aversion, risk aversion, status quo bias and lazyness leads to otherwise conscientious people keeping their savings in the bank. For them, any form of investment is deemed too risky, the topic too stress inducing to research or consider. Of course, inaction is also a decision and there is a thing called inflation - but you cannot put a price on your piece of mind./s
I realize the irony of writing about investments in 2020 - but when advising my best friend to buy gold (aka going long on fear) the response was "You know, I do not really believe in such things." I've raised the topic once with each of my friends, the lack of interest is almost universal. Paper just seems so much... safer... if you do not think about it.
and preferring it at... well, maybe never?
Never?!!!
You do realize never includes, but is not limited to, $1000, $100,000, $1,000,000 or, indeed, $3^^^3?
Never!!!!
I hope you won't take offence, but I don't know how else to say it - you have expressed a preference for the (let's say) certainty of winning $2 so extreme, that I find it hard to believe you would stick to it in practice.
Edit: formatting.
No, one shouldn't. Playing a game of chance once or a thousand times does not influence the outcome of the next round (aka the gambler's fallacy). If a bet is a good idea one time, it's a good idea a thousand times. And if a bet is a good idea a thousand times, it is a good idea the first time. How could you consider betting a thousand times to be a good idea, if you think each individual bet is a bad idea?
Gambler's ruin. The bets are the same, but you are not. If bets are rare enough or large enough, they do not justify they simplifying assumption of ergodicity ('adding up to normality' in this case) and greedy expected-value maximization is not optimal.
Correct. Which is why risk management and diversification are crucial and why you should never bet more than you can afford to lose. I have this as an implicit rule, but I should have mentioned it. Thank you for pointing this out.
Edit: And I should probably read up more on the Gambler's ruin. I can see how expected value maximization doesn't hold up in the extreme cases, but it had to be pointed to me first.
The bets are the same, but you are not. If bets are rare enough or large enough, they do not justify they simplifying assumption of ergodicity
Can you expand on this a little? I don't understand why the number of sequential bets you're offered makes it easier to assume ergodicity, or indeed changes optimal bet sizing at all. (I strongly agree with the rest of your post fwiw)
The "two ice cream cups from Hsee (1988)" image is broken -- I think it was hosted on old-LW and has now gone away. So I found the paper and uploaded a new copy of the image to imgur. Here it is.
This seems related to scope insensitivity. In talking about 200,000 dead birds, 200,000 has low evaluability. Same with having a 1/X chance of dying in a car crash.
It's also worth to note that while the recipient of a 1000$ watch will probably mention it in their will, the recipient of a 1000$ car will mention you in not-so-kind words whenever it breaks down. The same with the expensive scarf and coat: the scarf is likely warm, soft, stylish and durable, since it is an expensive one, while the coat is likely the opposite, thereby representing a far lower value than its price would suggest.
Of course, the number of entries in a dictionary is more important than whether it has a torn cover, at least if you ever plan on using it for anything.
If you plan on using it to decorate your shelf, the cover is essential.
With the expensive part of the Hallowthankmas season now approaching, a question must be looming large in our readers' minds:
I'm glad to report the answer is yes! According to Hsee (1998)—in a paper entitled "Less is better: When low-value options are valued more highly than high-value options"—if you buy someone a $45 scarf, you are more likely to be seen as generous than if you buy them a $55 coat.
This is a special case of a more general phenomenon. An earlier experiment, Hsee (1996), asked subjects how much they would be willing to pay for a second-hand music dictionary:
The gotcha was that some subjects saw both dictionaries side-by-side, while other subjects only saw one dictionary...
Subjects who saw only one of these options were willing to pay an average of $24 for Dictionary A and an average of $20 for Dictionary B. Subjects who saw both options, side-by-side, were willing to pay $27 for Dictionary B and $19 for Dictionary A.
Of course, the number of entries in a dictionary is more important than whether it has a torn cover, at least if you ever plan on using it for anything. But if you're only presented with a single dictionary, and it has 20,000 entries, the number 20,000 doesn't mean very much. Is it a little? A lot? Who knows? It's non-evaluable. The torn cover, on the other hand—that stands out. That has a definite affective valence: namely, bad.
Seen side-by-side, though, the number of entries goes from non-evaluable to evaluable, because there are two compatible quantities to be compared. And, once the number of entries becomes evaluable, that facet swamps the importance of the torn cover.
From Slovic et. al. (2002): Would you prefer:
While the average prices (equivalence values) placed on these options were $1.25 and $2.11 respectively, their mean attractiveness ratings were 13.2 and 7.5. Both the prices and the attractiveness rating were elicited in a context where subjects were told that two gambles would be randomly selected from those rated, and they would play the gamble with the higher price or higher attractiveness rating. (Subjects had a motive to rate gambles as more attractive, or price them higher, that they would actually prefer to play.)
The gamble worth more money seemed less attractive, a classic preference reversal. The researchers hypothesized that the dollar values were more compatible with the pricing task, but the probability of payoff was more compatible with attractiveness. So (the researchers thought) why not try to make the gamble's payoff more emotionally salient—more affectively evaluable—more attractive?
And how did they do this? By adding a very small loss to the gamble. The old gamble had a 7/36 chance of winning $9. The new gamble had a 7/36 chance of winning $9 and a 29/36 chance of losing 5¢. In the old gamble, you implicitly evaluate the attractiveness of $9. The new gamble gets you to evaluate the attractiveness of winning $9 versus losing 5¢.
"The results," said Slovic. et. al., "exceeded our expectations." In a new experiment, the simple gamble with a 7/36 chance of winning $9 had a mean attractiveness rating of 9.4, while the complex gamble that included a 29/36 chance of losing 5¢ had a mean attractiveness rating of 14.9.
A follow-up experiment tested whether subjects preferred the old gamble to a certain gain of $2. Only 33% of students preferred the old gamble. Among another group asked to choose between a certain $2 and the new gamble (with the added possibility of a 5¢ loss), fully 60.8% preferred the gamble. After all, $9 isn't a very attractive amount of money, but $9/5¢ is an amazingly attractive win/loss ratio.
You can make a gamble more attractive by adding a strict loss! Isn't psychology fun? This is why no one who truly appreciates the wondrous intricacy of human intelligence wants to design a human-like AI.
Of course, it only works if the subjects don't see the two gambles side-by-side.
Similarly, which of these two ice creams do you think subjects in Hsee (1998) preferred?
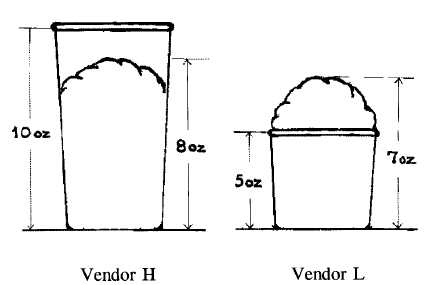
Naturally, the answer depends on whether the subjects saw a single ice cream, or the two side-by-side. Subjects who saw a single ice cream were willing to pay $1.66 to Vendor H and $2.26 to Vendor L. Subjects who saw both ice creams were willing to pay $1.85 to Vendor H and $1.56 to Vendor L.
What does this suggest for your holiday shopping? That if you spend $400 on a 16GB iPod Touch, your recipient sees the most expensive MP3 player. If you spend $400 on a Nintendo Wii, your recipient sees the least expensive game machine. Which is better value for the money? Ah, but that question only makes sense if you see the two side-by-side. You'll think about them side-by-side while you're shopping, but the recipient will only see what they get.
If you have a fixed amount of money to spend—and your goal is to display your friendship, rather than to actually help the recipient—you'll be better off deliberately not shopping for value. Decide how much money you want to spend on impressing the recipient, then find the most worthless object which costs that amount. The cheaper the class of objects, the more expensive a particular object will appear, given that you spend a fixed amount. Which is more memorable, a $25 shirt or a $25 candle?
Gives a whole new meaning to the Japanese custom of buying $50 melons, doesn't it? You look at that and shake your head and say "What is it with the Japanese?". And yet they get to be perceived as incredibly generous, spendthrift even, while spending only $50. You could spend $200 on a fancy dinner and not appear as wealthy as you can by spending $50 on a melon. If only there was a custom of gifting $25 toothpicks or $10 dust specks; they could get away with spending even less.
PS: If you actually use this trick, I want to know what you bought.
Hsee, C. K. (1996). The evaluability hypothesis: An explanation for preference reversals between joint and separate evaluations of alternatives. Organizational Behavior and Human Decision Processes, 67, 242-257.
Hsee, C. K. (1998). Less is better: When low-value options are valued more highly than high-value options. Journal of Behavioral Decision Making, 11, 107-121.
Slovic, P., Finucane, M., Peters, E. and MacGregor, D. (2002.) Rational Actors or Rational Fools: Implications of the Affect Heuristic for Behavioral Economics. Journal of Socio-Economics, 31: 329–342.