Not sure if this is what KevinGrant was referring to, but this article discusses the same phenomenon
http://rosettaproject.org/blog/02012/mar/1/language-speed-vs-density/
You say you are rejecting Von Neumann utility theory. Which axiom are you rejecting?
https://en.wikipedia.org/wiki/Von_Neumann–Morgenstern_utility_theorem#The_axioms
I think this is pretty cool and interesting, but I feel compelled to point out that all is not as it seems:
Its worth noting, though, that just the evaluation function is a neural network. The search, while no long iteratively deepening, is still recursive. Also, the evaluation function is not a pure neural network. It includes a static exchange evaluation.
It's also worth noting that doubling the amount of computing time usually increasing a chess engine's score by about 60 points. International masters usually have a rating below 2500. Though this is sketchy, the top chess engines are rated at around 3300. Thus, you could make a top-notch engine approximately 10,000 times slower and achieve the same performance.
Now, that 3300 figure is probably fairly inaccurate. Also, its quite possible that if the developer tweaked their recursive search algorithm, they could improve it. Thus that 10,000 figure I came to above is probably fairly inaccurate. Regardless, it is not clear to me that the neural network itself is proving terribly useful.
Just to clarify, I feel that what you're basically saying that often what is called the base-rate fallacy is actually the result of P(E|!H) being too high.
I believe this is why Bayesians usually talk not in terms of P(H|E) but instead use Bayes Factors.
Basically, to determine how strongly ufo-sightings imply ufos, don't look at P(ufos | ufo-sightings). Instead, look at P(ufos | ufo-sightings) / P(no-ufos | ufo-sightings).
This ratio is the Bayes factor.
I'm currently in debate and this is one of (minor) things that annoy me about it. The reason I can still enjoy debate (as a competitive endeavor) is that I treat it more like a game than an actual pursuit of truth.
I am curious though whether you think this actively harms peoples ability to reason or whether this just provides more numerous examples how most people reason - i.e. is this primarily a sampling problem?
Could we ever get evidence of a "read-only" soul? I'm imagining something that translates biochemical reactions associated with emotions into "actual" emotions. Don't get me wrong, I still consider myself an atheist, but it seems to me that how strongly one believes in a soul that is only affected by physical reality is based purely on their prior probability.
Thanks for taking the time to contribute!
I'm particularly interested in "Goals interrogation + Goal levels".
Out of curiosity, could you go a little more in-depth regarding what "How to human" would entail? Is it about social functioning? first aid? psychology?
I'd also be interested in "Memory and Notepads", as I don't really take notes outside of classes.
With "List of Effective Behaviors", would that be behaviors that have scientific evidence for achieving certain outcomes ( happiness, longevity, money, etc.), or would that primarily be anecdotal?
That last one "Strike to the heart of question" reminds me very much of the "void" from the 12 virtues, which always struck me as very important, but frustratingly vaguely described. I think you really hit the nail on the head with "am I giving the best answer to the best question I can give". I'm not really sure where you could go with this, but I'm eager to see.
Not sure if this is obvious of just wrong, but isn't it possible (even likely?) that there is no way of representing a complex mind that is sufficiently useful enough to allow an AI to usefully modify itself. For instance, if you gave me complete access to my source code, I don't think I could use it to achieve any goals as such code would be billions of lines long. Presumably there is a logical limit on how far one can usefully compress ones own mind to reason about it, and it seams reasonably likely that such compression will be too limited to allow a singularity.
What I mean by "essentially ignore" is that if you are (for instance) offered the following bet you would probably accept: "If you are in the first 100 rooms, I kill you. Otherwise, I give you a penny."
I see your point regarding the fact that updating using Bayes' theorem implies your prior wasn't 0 to begin with.
I guess my question is now whether there are any extended versions of probability theory. For instance, Kolmogorov probability reverts to Aristotelian logic for the extremes P=1 and P=0. Is there a system of though that revers to probability theory for finite worlds but is able to handle infinite worlds without privileging certain (small) numbers?
I will... (read more)
EDIT: I tested this idea in a simulation and it (un)fortunately failed.
This post is an attempt to combine some parts of frequentism with some parts of Bayesianism. Unfortunately, there is a good deal of probability theory. I assume that "improper priors" are okay to use and that we have no prior knowledge about the population of which we are trying to learn.
THEORY
Let's say we're trying to estimate some parameter, B. If we interpret the likelihood function as a conditional probability function, we get a function for our posterior probability density function after taking n samples:
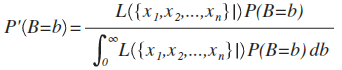
This yields an expected value of B:
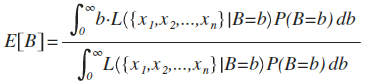
Now, intuitively, it would make a lot of sense if, given B=b,... (read 254 more words →)
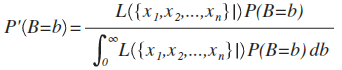
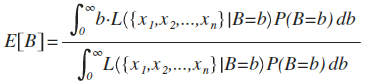
Since this seems like a question at the center of this whole thing, I just wanted to double check using other sources. Using [this](https://www.omnicalculator.com/health/tdee) calculator with the "little/no exercise" setting, I see
Female; 36; 5'4"
Weight: 65.5 kg -> 78 kg
TDEE: 1596 -> 1746
Diff: 150 kcal/d
If we set it to "moderate exercise", the gap increases to 194 kcal/d
[This](https://www.niddk.nih.gov/bwp) calculator yields similar results
So, pretty much in line with your conclusion.