Asymptotic Notation

Asymptotic Notation (Bachmann–Landau notation) is a notation for comparing the behavior of functions at extreme values – both very large, and very small. This is a convenient way to compare the performance of algorithms on large inputs, as well as the accuracy of approximations. This page will focus on the behavior at very large values, which is useful for analyzing the behavior of algorithms (both time and space requirements), rather than very minute values.

Asymptotic Behavior

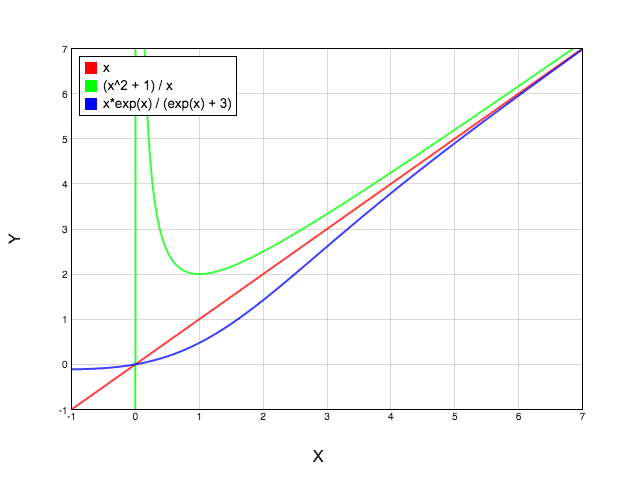
The asymptotic behavior of a function is its behavior as its input grows large.

For example, as x grows large, the three functions above all start to take on the same asymptotic behavior. Asymptotic notation gives a way to express the relationship between two functions' asymptotic behaviors.

Little-Oh

Suppose we have two functions f(x) and g(x). If

$${\forall }_c{\exists }_n\text{such that}{\forall }_{x>n}f\left(x\right)\le c\cdot g\left(x\right)$$

we say that $f\left(x\right)=o\left(g\right(x\left)\right)$ (spoken as "f is little oh of g"). In other words, no matter how we scale $g\left(x\right)$, it will eventually overtake $f\left(x\right)$. One can also say that $g\left(x\right)$ dominates $f\left(x\right)$, because, in the long run, $f\left(x\right)$ will become arbitrarily small compared to $g\left(x\right)$.

An equivalent definition is that $f\left(x\right)=o\left(g\right(x\left)\right)$ is true if (and only if)

$$\underset{x\to \infty }{lim}\frac{f\left(x\right)}{g\left(x\right)}=0$$.

A Note on Notation

While the standard notation uses an equal sign (i.e. $f\left(x\right)=o\left(g\right(x\left)\right)$), a more precise notation might be $f\left(c\right)\in o\left(g\right(x\left)\right)$, where $o\left(g\right(x\left)\right)$ is the set of functions that are, in some sense, smaller than $g\left(x\right)$ (asymptotically). Nonetheless, using an equal sign is customary, and is the notation that will be used here.

Properties of Little-Oh

1. $f\left(x\right)=o\left(f\right(x\left)\right)$ is always false
2. $f\left(x\right)=o\left(g\right(x\left)\right)⟹g\left(x\right)\ne o\left(f\right(x\left)\right)$
3. $f\left(x\right)=o\left(g\right(x\left)\right)\text{and}g\left(x\right)=o\left(h\right(x\left)\right)⟹f\left(x\right)=o\left(h\right(x\left)\right)$
4. $f\left(x\right)=o\left(g\right(x\left)\right)⟹c+f\left(x\right)=o\left(g\right(x\left)\right)$
5. $f\left(x\right)=o\left(g\right(x\left)\right)⟹c\cdot f\left(x\right)=o\left(g\right(x\left)\right)$
6. $f\left(x\right)=o\left(g\right(x\left)\right)⟺limx\to \infty \frac{f\left(x\right)}{g\left(x\right)}=0$

The first three properties are essentially the same properties required of a strict ordering, which means that this notation gives us a way to order functions by how quickly they grow, as x approaches infinity (see the "Common Functions" section)

The 4th and 5th properties show that asymptotic notation does not care about adding or multiplying by constants. This is useful in computer science, where constant factors may vary by hardware, programming language, and other variables that are often hard to talk about precisely; asymptotic notation gives computer scientists a way to analyze algorithms independent of the hardware that is running it.

The last property suggests a powerful way of determining the asymptotic behavior of two functions – in fact, combined with L'Hôpital's Rule, it is often all one needs.

Example

Example 1

Consider $f\left(x\right)=200x+10000$ and $g\left(x\right)=x^2$. Prove that $f\left(x\right)=o\left(g\right(x\left)\right)$.

$$limx\to \infty \frac{f\left(x\right)}{g\left(x\right)}=limx\to \infty \frac{200x+10000}{x^2}$$

Though this limit doesn't seem particularly approachable, L'Hôpital's Rule makes short work of it:

$$limx\to \infty \frac{200x+10000}{x^2}=limx\to \infty \frac{200}{2x}=0$$

Therefore, by property 7, $f\left(x\right)=o\left(g\right(x\left)\right)$.

Example 2

Let $f\left(x\right)=20x^2-10x+5$ and $g\left(x\right)=2x^3-x^2+10$. Again, we will use property 7, combined with L'Hôpital's Rule:

$$limx\to \infty \frac{f\left(x\right)}{g\left(x\right)}=limx\to \infty \frac{20x^2-10x+5}{2x^3-x^2+10}=limx\to \infty \frac{40x-10}{6x^2-2x}$$

Unlike the previous example, applying L'Hôpital's Rule doesn't seem to have reduced the fraction to an easily evaluable limit. Fortunately, we are welcome to apply L'Hôpital's Rule as many times as we like, without changing the value of the limit.

$$=limx\to \infty \frac{40}{12x}=limx\to \infty \frac{0}{12}=0$$

Therefore $f\left(x\right)=o\left(g\right(x\left)\right)$.

Common Functions

Functions that are frequently seen while analyzing algorithms are of particular use and interest. Because little-Oh notation suggests a strict ordering, the following functions are listed from smallest to largest, asymptotically.

1. $f\left(x\right)=1$
2. $f\left(x\right)=log\left(log\right(x\left)\right)$
3. $f\left(x\right)=log\left(x\right)$
4. $f\left(x\right)=x$
5. $f\left(x\right)=x\cdot log\left(x\right)$
6. $f\left(x\right)=x^{1+ϵ}$, $0<ϵ<1$
7. $f\left(x\right)=x^2$
8. $f\left(x\right)=x^3$
9. $f\left(x\right)=x^4$
10. ...
11. $f\left(x\right)=e^{cx}$
12. $f\left(x\right)=x!$

Theta

Given any particular function, it's generally pretty easy to find some function that grows asymptotically faster. For instance, given the function $f\left(x\right)=x^2$, one could claim $f\left(x\right)=o(x!)$. Nonetheless, the goal is to represent something useful about the function, which generally means bounding its asymptotic growth rate as tightly as possible. $f\left(x\right)=o\left(x^3\right)$ is better, while $f\left(x\right)=o\left(x^{2}log\right(x\left)\right)$ is even better than that.

The expression $f\left(x\right)=\Theta \left(g\right(x\left)\right)$ states that $f\left(x\right)$ and $g\left(x\right)$ grow at an asymptotically similar rate. In other words

$$0<\underset{x\to \infty }{lim}\frac{f\left(x\right)}{g\left(x\right)}<\infty$$

A simple example is $f\left(x\right)=x^2$ and $g\left(x\right)=3x^2$. Here, ${lim}_{x\to \infty }\frac{f\left(x\right)}{g\left(x\right)}=\frac{1}{3}$, which, as promised, is between zero and infinity.

Big-Oh

Little-Oh and Little-Omega

Use in Computer Science

Bounding Error