Quick comment one:
This jumped out instantly when I looked at the charts: Your prior and evidence can't possibly both be correct at the same time. Everywhere the prior has non-negligible density has negligible likelihood. Everywhere that has substantial likelihood has negligible prior density. If you try multiplying the two together to get a compromise probability estimate instead of saying "I notice that I am confused", I would hold this up as a pretty strong example of the real sin that I think this post should be arguing against, namely that of trying to use math too blindly without sanity-checking its meaning.
Quick comment two:
I'm a major fan of Down-To-Earthness as a virtue of rationality, and I have told other SIAI people over and over that I really think they should stop using "small probability of large impact" arguments. I've told cryonics people the same. If you can't argue for a medium probability of a large impact, you shouldn't bother.
Part of my reason for saying this is, indeed, that trying to multiply a large utility interval by a small probability is an argument-stopper, an attempt to shut down further debate, and someone is justified in hav...
I don't consider myself to be multiplying small probabilities by large utility intervals at any point in my strategy
What about people who do think SIAI's probability of success is small? Perhaps they have different intuitions about how hard FAI is, or don't have enough knowledge to make an object-level judgement so they just apply the absurdity heuristic. Being one of those people, I think it's still an important question whether it's rational to support SIAI given a small estimate of probability of success, even if SIAI itself doesn't want to push this line of inquiry too hard for fear of signaling that their own estimate of probability of success is low.
Leaving aside Aumann questions: If people like that think that the Future of Humanity Institute, work on human rationality, or Giving What We Can has a large probability of catalyzing the creation of an effective institution, they should quite plausibly be looking there instead. "I should be doing something I think is at least medium-probably remedying the sheerly stupid situation humanity has gotten itself into with respect to the intelligence explosion" seems like a valuable summary heuristic.
If you can't think of anything medium-probable, using that as an excuse to do nothing is unacceptable. Figure out which of the people trying to address the problem seem most competent and gamble on something interesting happening if you give them more money. Money is the unit of caring and I can't begin to tell you how much things change when you add more money to them. Imagine what the global financial sector would look like if it was funded to the tune of $600,000/year. You would probably think it wasn't worth scaling up Earth's financial sector.
If you can't think of anything medium-probable, using that as an excuse to do nothing is unacceptable.
That's my gut feeling as well, but can we give a theoretical basis for that conclusion, which might also potentially be used to convince people who can't think of anything medium-probable to "do something"?
My current thoughts are
I think the creation of smarter-than-human intelligence has a (very) large probability of an (extremely) large impact, and that most of the probability mass there is concentrated into AI
That's the probability statement in his post. He didn't mention the probability of SIAI's success, and hasn't previously when I've emailed him or asked in public forums, nor has he at any point in time that I've heard. Shortly after I asked, he posted When (Not) To Use Probabilities.
SIAI-now is fucked up (and SIAI-future very well will be too). (I won't substantiate that claim here.)
Will you substantiate it elsewhere?
Regarding the graphs, I assumed that they were showing artificial examples so that we could viscerally understand at a glance what the adjustment does, not that this is what the prior and evidence should look like in a real case.
I disagree. It can be rational to shift subjective probabilities by many orders of magnitude in response to very little new information.
What your example looks like is a nearly uniform prior over a very large space- nothing's wrong when we quickly update to believe that yesterday's lottery numbers are 04-15-21-31-36.
But the point where you need to halt, melt, and catch fire is if your prior assigns the vast majority of the probability mass to a small compact region, and then the evidence comes along and lands outside that region. That's the equivalent of starting out 99.99% confident that you know tomorrow's lottery numbers will begin with 01-02-03, and being proven wrong.
(Please don't upvote this comment till you've read it fully; I'm interpreting upvotes in a specific way.) Question for anyone on LW: If I had a viable preliminary Friendly AI research program, aimed largely at doing the technical analysis necessary to determine as well as possible the feasibility and difficulty of Friendly AI for various values of "Friendly", and wrote clearly and concretely about the necessary steps in pursuing this analysis, and listed and described a small number of people (less than 5, but how many could actually be convinced to focus on doing the analysis would depend on funds) who I know of who could usefully work on such an analysis, and committed to have certain summaries published online at various points (after actually considering concrete possibilities for failure, planning fallacy, etc., like real rationalists should), and associated with a few (roughly 5) high status people (people like Anders Sandberg or Max Tegmark, e.g. by convincing them to be on an advisory board), would this have a decent chance of causing you or someone you know to donate $100 or more to support this research program? (I have a weird rather mixed reputation among the ...
I have a weird rather mixed reputation among the greater LW community, so if that affects you negatively please pretend that someone with a more solid reputation but without super high karma is asking this question, like Steven Kaas.
Unless you would be much less involved in this potential program than the comment indicates, this seems like an inappropriate request. If people view you negatively due to your posting history, they should absolutely take that information into account in assessing how likely they would be to provide financial support to such a program (assuming that the negative view is based on relevant considerations such as your apparent communication or reasoning skills as demonstrated in your comments).
Fair enough, but in light of your phrasing in both the original comment ("If I [did the following things]") and your comment immediately following it (quoted below; emphasis added), it certainly appeared to me that you seemed to be describing a significant role for yourself, even though your proposal was general overall.
(Some people, including me, would really like it if a competent and FAI-focused uber-rationalist non-profit existed. I know people who will soon have enough momentum to make this happen. I am significantly more familiar with the specifics of FAI (and of hardcore SingInst-style rationality) than many of those people and almost anyone else in the world, so it'd be necessary that I put a lot of hours into working with those who are higher status than me and better at getting things done but less familiar with technical Friendliness. But I have many other things I could be doing. Hence the question.)
I think the problem here is that your posting style, to be frank, often obscures your point.
In most cases, posts that consist of a to-the-point answer followed by longer explanations use the initial statement to make a concise case. For instance, in this post, my first sentence sums up what I think about the situation and the rest explains that thought in more detail so as to convey a more nuanced impression.
By contrast, when Eliezer asked "What's the output here that the money is paying for," your first sentence was "Money would pay for marginal output, e.g. in the form of increased collaboration, I think, since the best Friendliness-cognizant x-rationalists would likely already be working on similar things." This does not really answer his question, and while you clarify this with your later points, the overall message is garbled.
The fact that your true answer is buried in the middle of a paragraph does not really help things much. Though I can see what you are trying to say, I can't in good and honest conscience describe it as clear. Had you answered, on the other hand, "Money would pay for the technical analysis necessary to determine as well as possible the feasibility and difficulty of FAI..." as your first sentence, I think your post would have been more clear and more likely to be understood.
It's hardly fair to blame the reader when you've got "sentences" like this:
I think that my original comment was at roughly the most accurate and honest level of vagueness (i.e. "aimed largely [i.e. primarily] at doing the technical analysis necessary to determine as well as possible the feasibility and difficulty [e.g. how many Von Neumanns, Turings, and/or Aristotles would it take?] of Friendly AI for various (logical) probabilities of Friendliness [e.g. is the algorithm meta-reflective enough to fall into (one of) some imagined Friendliness attractor basin(s)?]").
Unfortunately that is not currently possible for many reasons, including some large ones I can't talk about and that I can't talk about why I can't talk about.
Why can't you talk about why you can't talk about them?
I'm not a big fan of the appeal to secret reasons, so I think I'm going to have pull out of this discussion. I will note, however, that you personally seem to be involved in more misunderstandings than the average LW poster, so while it's certainly possible that your secret reasons are true and valid and Eliezer just sucks at reading or whatever, you may want to clarify certain elements of your own communication as well.
I unfortunately predict that "going more meta" will not be strongly received here.
They're not currently doing any research on Friendly AI, and their political situation is such that I don't expect them to be able to do so effectively for a while, if ever.
My understanding is that SIAI recently tried to set up a new in-house research team to do preliminary research into FAI (i.e., not try to build an FAI yet, but just do whatever research that might be eventually helpful to that project). This effort didn't get off the ground, but my understanding again is that it was because the researchers they tried to recruit had various reasons for not joining SIAI at this time. I was one of those they tried to recruit, and while I don't know what the others' reasons were, mine were mostly personal and not related to politics.
You must also know all this, since you were involved in this effort. So I'm confused why you say SIAI won't be doing effective research on FAI due to its "political situation". Did the others not join SIAI because they thought SIAI was in a bad political situation? (This seems unlikely to me.) Or are you referring to the overall lack of qualified, recruitable researchers as a "political situation"? If you are, why do you think this new organization would be able to do better?
(Or did you perhaps not learn the full story, and thought SIAI stopped this effort for political reasons?)
I was trying to quickly gauge vague interest in a vague notion.
I won't give that evidence here.
(I won't substantiate that claim here.)
I will not clarify this.
The answer to your question isn't among your list of possible answers.
I find this stressful; it's why I make token attempts to communicate in extremely abstract or indirect ways with Less Wrong, despite the apparent fruitlessness. But there's really nothing for it.
If you can't say anything, don't say anything.
I like this post, but I think that it suffers from two things that make it badly written:
Many times (starting with the title) the phrasing chosen suggests that you are attacking the basic decision-theoretic principle that one should the take the action with the highest expected utility (or give to the charity with the highest expected marginal value resulting from the donation). But you're not attacking this; you're attacking a way to incorrectly calculate expected utility by using only information that can be easily quantified and leaving out information that's harder to quantify. This is certainly a correct point, and a good one to make, but it's not the point that the title suggests, and many commenters have already been confused by this.
Pascal's mugging should be left out entirely. For one thing, it's a deliberately counterintuitive situation, so your point that we should trust our intuitions (as manifestations of our unquantifiable prior) doesn't obviously apply here. Furthermore, it's clear that the outcome of not giving the mugger money is not normally (or log-normally) distributed, with a decent chance of producing any value between 0 and 2X. In fact, it's a bimoda
I'm pretty sure that I endorse the same method you do, and that the "EEV" approach is a straw man.
It's also the case that while I can endorse "being hesitant to embrace arguments that seem to have anti-common-sense implications (unless the evidence behind these arguments is strong) ", I can't endorse treating the parts of an argument that lack strong evidence (e.g. funding SIAI is the best way to help FAI) as justifications for ignoring the parts that have strong evidence (e.g. FAI is the highest EV priority around). In a case like that, the rational thing to do is to investigate more or find a third alternative, not to go on with business as usual.
I'm pretty sure that I endorse the same method you do, and that the "EEV" approach is a straw man.
The post doesn't highlight you as an example of someone who uses the EEV approach and I agree that there's no evidence that you do so. That said, it doesn't seem like the EEV approach under discussion is a straw man in full generality. Some examples:
As lukeprog mentions, Anna Salamon gave the impression of using the EEV approach in one of her 2009 Singularity Summit talks.
One also sees this sort of thing on LW from time to time, e.g. [1], [2].
As Holden mentions, the issue came up in the 2010 exchange with Giving What We Can.
Thus, when aiming to maximize expected positive impact, it is not advisable to make giving decisions based fully on explicit formulas.
I love that you don't seem to argue against maximizing EV, but rather to argue that a certain method, EEV, is a bad way to maximize EV. If this was stated at the beginning of the article I would have been a lot less initially skeptical.
Here's what I think is true and important about this post: some people will try to explicitly estimate expected values in ways that don't track the real expected values, and when they do this, they'll make bad decisions. We should avoid these mistakes, which may be easy to fall into, and we can avoid some of them by using regressions of the kind described above in the case of charity cost-effectiveness estimates. As Toby points out, this is common ground between GiveWell and GWWC. Let me list a what I take to be a few points of disagreement.
I think that after making an appropriate attempt to gather evidence, the result of doing the best expected value calculation that you can is by far the most important input into a large scale philanthropic decision. We should think about the result of the calculation makes sense, we should worry if it is wildly counterintuitive, and we should try hard to avoid mistakes. But the result of this calculation will matter more than most kinds of informal reasoning, especially if the differences in expected value are great. I think this will be true for people who are competent with thinking in terms of subjective probabilities and expected value...
The majority of the work that this adjustment does is due to the assumption that an action with high variance is practically as likely to greatly harm as to greatly help, and thus the long positive tail is nearly canceled out by the long negative tail. For some Pascal's Muggings (like the original Wager), this may be valid, but for others it's not.
If Warren Buffett offers to play a hand of poker with you, no charge if he wins and he gives you a billion if he loses, some skepticism about the setup might be warranted- but to say "it would be better for me if we played for $100 of your money instead" seems preposterous. (Since in this case there's no negative tail, an adjustment based only on mean and variance is bound to screw up.)
...and an asteroid-prevention program is extremely likely to either do nothing or save the whole world. Modeling it with a normal distribution means pretending that it's almost as likely to cause billions of deaths (compared to the baseline of doing nothing) as it is to save billions of lives.
This post seems confused about utility maximisation.
It's possible for an argument to fail to consider some evidence and so mislead, but this isn't a problem with expected utility maximisation, it's just assigning an incorrect distribution for the marginal utilities. Overly formal analyses can certainly fail for real-world problems, but half-Bayesian ad-hoc mathematics won't help.
EDIT: The mathematical meat of the post is the linked-to analysis done by Dario Amodei. This is perfectly valid. But the post muddies the mathematics by comparing the unbiased measurement considered in that analysis with estimates of charities' worth. The people giving these estimates will have already used their own priors, and so you should only adjust their estimates to the extent to which your priors differ from theirs.
I was having trouble understanding the first example of EEV, until I read this part of Will Crouch's original comment:
We tend to assume, in the absence of other information, that charities are average at implementing their intervention, whereas you seem to assume that charities are bad at implementing their intervention, until you have been shown concrete evidence that they are not bad at implementing their intervention.
I agree this is wrong. They failed to consider that charities that are above average will tend to make information available showing that they are above average, so absence of information in this case is Bayesian evidence that a charity is below average. Relevant LW post: http://lesswrong.com/lw/ih/absence_of_evidence_is_evidence_of_absence/
This seems so vague and abstract.
Let me suggest a concrete example: the existential risk of asteroid impacts. It is pretty easy to estimate the distribution of time till the next impact big enough to kill all humans. Astronomy is pretty well understood, so it is pretty easy to estimate the cost of searching the sky for dangerous objects. If you imagine this as an ongoing project, there is the problem of building lasting organizations. In the unlikely event that you find an object that will strike in a year, or in 30, there is the more difficult problem of estimating the chance it will be dealt with.
It would be good to see your take on this example, partly to clarify this article and partly to isolate some objections from others.
This was, in fact, the first example I ever brought Holden. IMHO he never really engaged with it, but he did find it interesting and maintained correspondence which brought him to the FAI point. (all this long before I was formally involved with SIAI)
How Not To Sort By Average Ranking explains how you should actually choose which restaurant to go to. BeerAdvocate's method is basically a hack, with no general validity. Why is the minimum number of review ten? That number should in fact depend on the variance of reviews, I think.
That's precisely why it is arbitrary -- it's a cultural artifact, not an inherently meaningful level.
but because it is the standard value, you can be more confident that they didn't "shop around" for the p value that was most convenient for the argument they wanted to make. It's the same reason people like to see quarterly data for a company's performance - if a company is trying to raise capital and reports its earnings for the period "January 6 - April 12", you can bet that there were big expenses on January 5 and April 13 that they'd rather not include. This is much less of a worry if they are using standard accounting periods.
Hello all,
Thanks for the thoughtful comments. Without responding to all threads, I'd like to address a few of the themes that came up. FYI, there are also interesting discussions of this post at The GiveWell Blog , Overcoming Bias , and Quomodocumque (the latter includes Terence Tao's thoughts on "Pascal's Mugging").
On what I'm arguing. There seems to be confusion on which of the following I am arguing:
(1) The conceptual idea of maximizing expected value is problematic.
(2) Explicit estimates of expected value are problematic and can't be taken literally.
(3) Explicit estimates of expected value are problematic/can't be taken literally when they don't include a Bayesian adjustment of the kind outlined in my post.
As several have noted, I do not argue (1). I do aim to give with the aim of maximizing expected good accomplished, and in particular I consider myself risk-neutral in giving.
I strongly endorse (3) and there doesn't seem to be disagreement on this point.
I endorse (2) as well, though less strongly than I endorse (3). I am open to the idea of formally performing a Bayesian adjustment, and if this formalization is well done enough, taking the adjusted expected-value est...
Interesting! But let's go back to the roots...
You're proposing to equip an agent with a prior over the effectiveness of its actions instead of (in addition to?) a prior over possible worlds. Will such an agent be Bayesian-rational, or will it exhibit weird preference reversals? If the latter, do you see that as a problem? If the former, Bayesian-rationality means the agent must behave as though its actions were governed only by some prior over possible worlds; what does that prior look like?
This is classic. "Should I give him a dollar, or kill him as quickly as possible? [insert abstract consequentialist reasoning.] So I think I'll kill him as quickly as possible."
It's intuitively plausible that a Solomonoff type prior would (at least approximately) yield such an assumption.
But even if "intuitively plausible" equates to, say, 0.9999 probability, that's insufficient to disarm Pascal's Mugging. I think there's at least 0.0001 chance that a better approximate prior distribution for "value of an action" is one with a "heavy tail", e.g., one with infinite variance.
Minor tweaks suggested...
There are some formatting issues. For example there is an extra space below the heading 'The approach we oppose: "explicit expected-value" (EEV) decisionmaking' instead of above it, and the heading 'Informal objections to EEV decisionmaking' is just blended into the middle of a paragraph, along with the first sentence below it. The heading 'Approaches to Bayesian adjustment that I oppose' is formatted differently than the others are.
Use 'a' instead of 'an' here:
pre-existing view of how cost-effective an donation
Add 'and' before '(b)' here:
(a) have significant room for error (b) ...
You may want to add 'marginal' before 'value' here; I'm not sure that EEV proponents neglect the issue of marginal value:
I estimate that each dollar spent on Program P has a value of V
In this paragraph, you may want to link to this video as an example:
We've encountered numerous people who argue that charities working on reducing the risk of sudden human extinction must be the best ones to support...
For example, at 7:15 in the video, Anna says:
...Don't be afraid to write down estimates, even if the unknowns are very large, or even if you don't know very muc
I think other commenters have had a similar idea, but here's one way to say it.
It seems to me that the proposition you are attacking is not exactly the one you think you are attacking. I think you think you are attacking the proposition "charitable donations should be directed to the highest EV use, regardless of the uncertainty around the EV, as long as the EV estimate is unbiased," when the proposition you are really attacking is "the analysis generating some of these very uncertain, but very high EV effect estimates is flawed, and the tru...
I have a number of issues with your criticisms of EEV
In such a world, when people decided that a particular endeavor/action had outstandingly high EEV, there would (too often) be no justification for costly skeptical inquiry of this endeavor/action.
I'm not sure this is true, sceptical inquiry can have a high expected value when it helps you work out what is a better use of limited resources. In particular, my maths might be wrong, but I think that in a case with an action that has low probability of producing a large gain, any investigation that will c...
The article seems to be well written, clearly structured, honest with no weasel words, with concrete examples and graphs - all symptoms of a great post. In the same time, I am not sure what it is precisely saying. So I am confused.
The initial description of EEV seems pretty standard: calculate the expected gain from all possible actions and choose the best one. Then, the article criticises that approach as incorrect, giving examples like this:
...It seems fairly clear that a restaurant with 200 Yelp reviews, averaging 4.75 stars, ought to outrank a restaura
Upvoted.
I got that feeling after reading this. "Man, this sounds like common sense, and I've never thought about it like this before." - The mark of a really good argument.
Best article on LW in recent memory. Thank you for cross-posting it, and for your work with GiveWell.
I don't have many upvotes to give you, but I will shake down my budget and see what if anything I can donate.
Disclosure: I have done volunteer work for GiveWell and have discussed the possibility of taking a job with GiveWell at some point in the future.
Your stated prior would cause you to ignore even strong evidence in favour of an existential risk charity. It is therefore wrong (at least in this domain).
I'm not sure I'm intuiting the transformation to and from log-normals. My intuition is that since the mean of a log-normal with location u scale s is e^(u+s^2/2) rather than e^u, when we end up with a mean log, transforming back into a mean tacks the s^2/2 back on (aka we're back to value ~ X rather than value ~ 0). Maybe I'm missing something, I haven't gone through to rederive your results, but even if everything's right I think the math could be made more clear.
Great post! We need to see this kind of reasoning made explicit!
I don't understand the calculations used in the pascal's mugging section. would you please provide some more examples where all the calculations are explicit?
"Philanthropy’s Success Stories"
...I see impressive choices of causes and organizations; I don’t see impressive “tactics,” i.e., choices of projects or theories of change. This may simply be a reflection of the Casebook’s choice of approach and focus. There are many cases in which I found myself agreeing with the Casebook that a foundation had chosen an important and overlooked problem to put its money toward, but few (if any) cases where its strategy within the sector seemed particularly intricate, clever, noteworthy or crucial to its success. Th
The crucial characteristic of the EEV approach is that it does not incorporate a systematic preference for better-grounded estimates over rougher estimates. It ranks charities/actions based simply on their estimated value, ignoring differences in the reliability and robustness of the estimates.
Uncertainty in estimates of the expected value of an intervention tend to have the effect of naturally reducing it - since there are may ways to fail and few ways to succeed.
For instance think about drug trials. If someone claims that their results say there's a ...
just under 1/X.
That's a beautiful result, and it certainly feels like the calculation passes the "adds to normality" test. Thanks for the great post!
Relevant earlier paper with much the same idea but on existential risks: "Probing the Improbable: Methodological Challenges for Risks with Low Probabilities and High Stakes"
An interesting mathematical response: https://johncarlosbaez.wordpress.com/2011/08/19/bayesian-computations-of-expected-utility/
A bit late, but I think it is worth distinguishing two types of adjustments in this post. Typically, we evaluate alternative actions in terms of achieving a proxy goal, such as preventing deaths due to a particular disease. We attempt to compute the expected effect on the proxy goal of the alternatives. One adjustment is uncertainty in that calculation, such as whether the intervention works in theory, whether the charity is competent to carry it out, whether the charity has room for additional funding.
The other kind of adjustment is uncertainty in matchi...
There seems to be nothing in EEV that penalizes relative ignorance or relatively poorly grounded estimates, or rewards investigation and the forming of particularly well grounded estimates. If I can literally save a child I see drowning by ruining a $1000 suit, but in the same moment I make a wild guess that this $1000 could save 2 lives if put toward medical research, EEV seems to indicate that I should opt for the latter.
I don't understand this objection. What sort of subjective probability are we meant to be ascribing to the 'wild guess'? If less tha...
Did I summarize your point correctly:
Edit: not saying that I agree with this, just checking if my understanding is not off-base.
I have been waiting for someone to formalize this objection to Pascal's mugging for a long time, and I'm very happy that now that it's been done it's been done very well.
???
What precisely is the objection to Pascal's Mugging in the post? Just that the probability for the mugger being able to deliver goes down with N? This objection has been given thousands of times, and the counter response is that the probability can't go down fast enough to outweigh increase in utility. This is formalised here.
On the 'Yelp' examples: I looked at the yelp.com website, and it appears that it lets you rate things on a scale of 1 to 5 stars.
A thing with 200 reviews and an average of 4.75 seems like an example of humongous ballot-stuffing. Either that or nearly everyone on yelp.com votes 4 or 5 nearly all the time, so either way the example seems a bad one.
I'm pretty sure that I endorse the same method you do, and that the "EEV" approach is a straw man.
It's also the case that while I can endorse "being hesitant to embrace arguments that seem to have anti-common-sense implications (unless the evidence behind these arguments is strong) ", I can't endorse treating the parts of an argument that lack strong evidence (e.g. funding SIAI is the best way to help FAI) as justifications for ignoring the parts that have strong evidence (e.g. FAI is the highest EV priority around). In a case like that, the rational thing to do is to investigate more or find a third alternative, not to go on with business as usual.
I can't endorse treating the parts of an argument that lack strong evidence (e.g. funding SIAI is the best way to help FAI) as justifications for ignoring the parts that have strong evidence (e.g. FAI is the highest EV priority around). In a case like that, the rational thing to do is to investigate more or find a third alternative, not to go on with business as usual.
Agree here. Do you think that there's a strong case for direct focus on the FAI problem rather than indirectly working toward FAI via nuclear deproliferation [1] [2]? If so I'd be interest...
Note: I am cross-posting this GiveWell Blog post, after consulting a couple of community members, because it is relevant to many topics discussed on Less Wrong, particularly efficient charity/optimal philanthropy and Pascal's Mugging. The post includes a proposed "solution" to the dilemma posed by Pascal's Mugging that has not been proposed before as far as I know. It is longer than usual for a Less Wrong post, so I have put everything but the summary below the fold. Also, note that I use the term "expected value" because it is more generic than "expected utility"; the arguments here pertain to estimating the expected value of any quantity, not just utility.
While some people feel that GiveWell puts too much emphasis on the measurable and quantifiable, there are others who go further than we do in quantification, and justify their giving (or other) decisions based on fully explicit expected-value formulas. The latter group tends to critique us - or at least disagree with us - based on our preference for strong evidence over high apparent "expected value," and based on the heavy role of non-formalized intuition in our decisionmaking. This post is directed at the latter group.
We believe that people in this group are often making a fundamental mistake, one that we have long had intuitive objections to but have recently developed a more formal (though still fairly rough) critique of. The mistake (we believe) is estimating the "expected value" of a donation (or other action) based solely on a fully explicit, quantified formula, many of whose inputs are guesses or very rough estimates. We believe that any estimate along these lines needs to be adjusted using a "Bayesian prior"; that this adjustment can rarely be made (reasonably) using an explicit, formal calculation; and that most attempts to do the latter, even when they seem to be making very conservative downward adjustments to the expected value of an opportunity, are not making nearly large enough downward adjustments to be consistent with the proper Bayesian approach.
This view of ours illustrates why - while we seek to ground our recommendations in relevant facts, calculations and quantifications to the extent possible - every recommendation we make incorporates many different forms of evidence and involves a strong dose of intuition. And we generally prefer to give where we have strong evidence that donations can do a lot of good rather than where we have weak evidence that donations can do far more good - a preference that I believe is inconsistent with the approach of giving based on explicit expected-value formulas (at least those that (a) have significant room for error (b) do not incorporate Bayesian adjustments, which are very rare in these analyses and very difficult to do both formally and reasonably).
The rest of this post will:
The approach we oppose: "explicit expected-value" (EEV) decisionmaking
We term the approach this post argues against the "explicit expected-value" (EEV) approach to decisionmaking. It generally involves an argument of the form:
Examples of the EEV approach to decisionmaking:
The crucial characteristic of the EEV approach is that it does not incorporate a systematic preference for better-grounded estimates over rougher estimates. It ranks charities/actions based simply on their estimated value, ignoring differences in the reliability and robustness of the estimates. Informal objections to EEV decisionmaking There are many ways in which the sort of reasoning laid out above seems (to us) to fail a common sense test.
In the remainder of this post, I present what I believe is the right formal framework for my objections to EEV. However, I have more confidence in my intuitions - which are related to the above observations - than in the framework itself. I believe I have formalized my thoughts correctly, but if the remainder of this post turned out to be flawed, I would likely remain in objection to EEV until and unless one could address my less formal misgivings.
Simple example of a Bayesian approach vs. an EEV approach
It seems fairly clear that a restaurant with 200 Yelp reviews, averaging 4.75 stars, ought to outrank a restaurant with 3 Yelp reviews, averaging 5 stars. Yet this ranking can't be justified in an EEV-style framework, in which options are ranked by their estimated average/expected value. How, in fact, does Yelp handle this situation?
Unfortunately, the answer appears to be undisclosed in Yelp's case, but we can get a hint from a similar site: BeerAdvocate, a site that ranks beers using submitted reviews. It states:
In other words, BeerAdvocate does the equivalent of giving each beer a set number (currently 10) of "average" reviews (i.e., reviews with a score of 3.66, which is the average for all beers on the site). Thus, a beer with zero reviews is assumed to be exactly as good as the average beer on the site; a beer with one review will still be assumed to be close to average, no matter what rating the one review gives; as the number of reviews grows, the beer's rating is able to deviate more from the average.
To illustrate this, the following chart shows how BeerAdvocate's formula would rate a beer that has 0-100 five-star reviews. As the number of five-star reviews grows, the formula's "confidence" in the five-star rating grows, and the beer's overall rating gets further from "average" and closer to (though never fully reaching) 5 stars.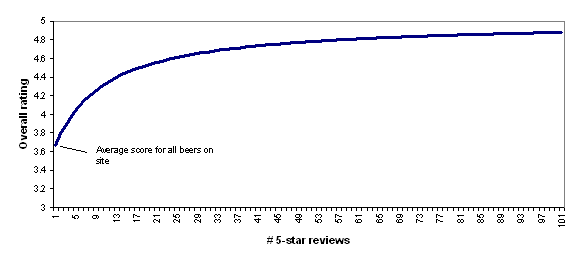
I find BeerAdvocate's approach to be quite reasonable and I find the chart above to accord quite well with intuition: a beer with a small handful of five-star reviews should be considered pretty close to average, while a beer with a hundred five-star reviews should be considered to be nearly a five-star beer.
However, there are a couple of complications that make it difficult to apply this approach broadly.
Applying Bayesian adjustments to cost-effectiveness estimates for donations, actions, etc.
As discussed above, we believe that both Giving What We Can and Back of the Envelope Guide to Philanthropy use forms of EEV analysis in arguing for their charity recommendations. However, when it comes to analyzing the cost-effectiveness estimates they invoke, the BeerAdvocate formula doesn't seem applicable: there is no "number of reviews" figure that can be used to determine the relative weights of the prior and the estimate.
Instead, we propose a model in which there is a normally (or log-normally) distributed "estimate error" around the cost-effectiveness estimate (with a mean of "no error," i.e., 0 for normally distributed error and 1 for lognormally distributed error), and in which the prior distribution for cost-effectiveness is normally (or log-normally) distributed as well. (I won't discuss log-normal distributions in this post, but the analysis I give can be extended by applying it to the log of the variables in question.) The more one feels confident in one's pre-existing view of how cost-effective an donation or action should be, the smaller the variance of the "prior"; the more one feels confident in the cost-effectiveness estimate itself, the smaller the variance of the "estimate error."
Following up on our 2010 exchange with Giving What We Can, we asked Dario Amodei to write up the implications of the above model and the form of the proper Bayesian adjustment. You can see his analysis here. The bottom line is that when one applies Bayes's rule to obtain a distribution for cost-effectiveness based on (a) a normally distributed prior distribution (b) a normally distributed "estimate error," one obtains a distribution with
The following charts show what this formula implies in a variety of different simple hypotheticals. In all of these, the prior distribution has mean = 0 and standard deviation = 1, and the estimate has mean = 10, but the "estimate error" varies, with important effects: an estimate with little enough estimate error can almost be taken literally, while an estimate with large enough estimate error ends ought to be almost ignored.
In each of these charts, the black line represents a probability density function for one's "prior," the red line for an estimate (with the variance coming from "estimate error"), and the blue line for the final probability distribution, taking both the prior and the estimate into account. Taller, narrower distributions represent cases where probability is concentrated around the midpoint; shorter, wider distributions represent cases where the possibilities/probabilities are more spread out among many values. First, the case where the cost-effectiveness estimate has the same confidence interval around it as the prior: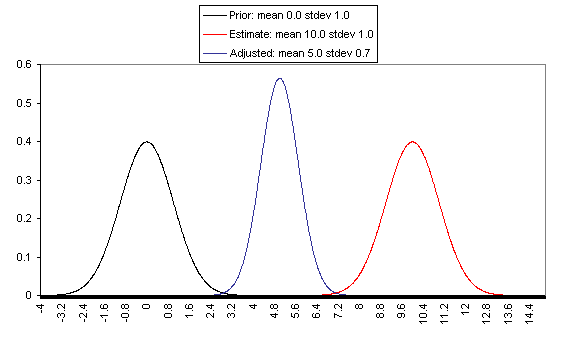
If one has a relatively reliable estimate (i.e., one with a narrow confidence interval / small variance of "estimate error,") then the Bayesian-adjusted conclusion ends up very close to the estimate. When we estimate quantities using highly precise and well-understood methods, we can use them (almost) literally.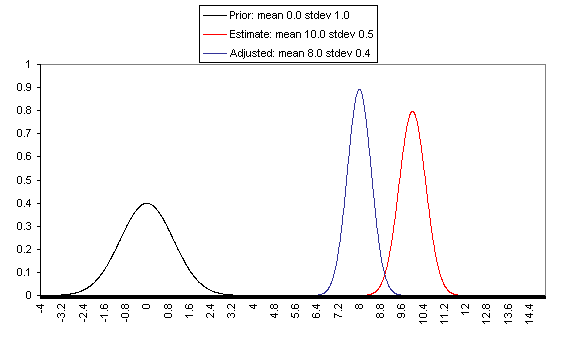
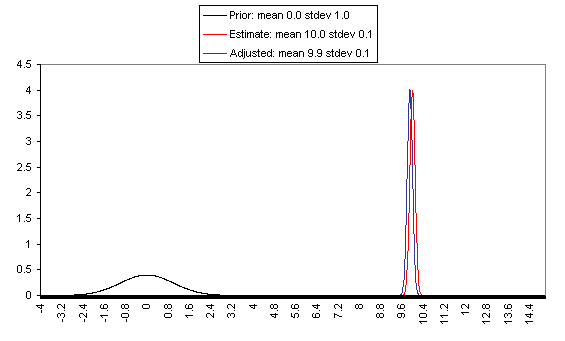
On the flip side, when the estimate is relatively unreliable (wide confidence interval / large variance of "estimate error"), it has little effect on the final expectation of cost-effectiveness (or whatever is being estimated). And at the point where the one-standard-deviation bands include zero cost-effectiveness (i.e., where there's a pretty strong probability that the whole cost-effectiveness estimate is worthless), the estimate ends up having practically no effect on one's final view.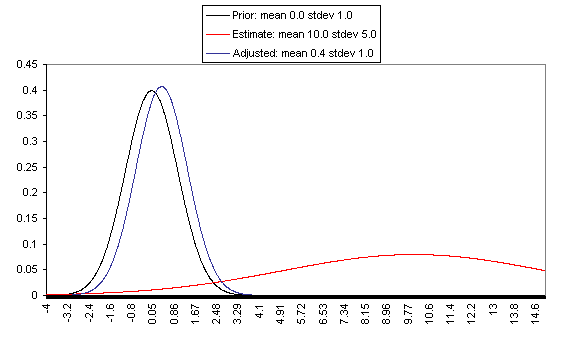
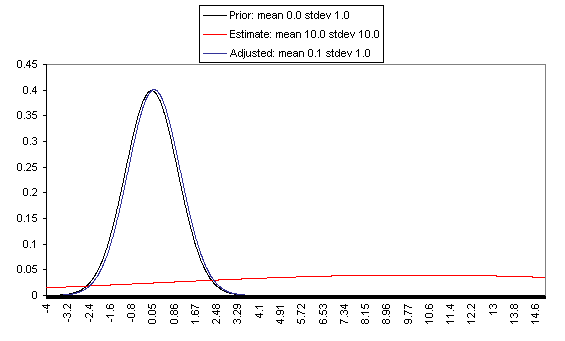
The details of how to apply this sort of analysis to cost-effectiveness estimates for charitable interventions are outside the scope of this post, which focuses on our belief in the importance of the concept of Bayesian adjustments. The big-picture takeaway is that just having the midpoint of a cost-effectiveness estimate is not worth very much in itself; it is important to understand the sources of estimate error, and the degree of estimate error relative to the degree of variation in estimated cost-effectiveness for different interventions.
Pascal's Mugging
Pascal's Mugging refers to a case where a claim of extravagant impact is made for a particular action, with little to no evidence:
Non-Bayesian approaches to evaluating these proposals often take the following form: "Even if we assume that this analysis is 99.99% likely to be wrong, the expected value is still high - and are you willing to bet that this analysis is wrong at 99.99% odds?"
However, this is a case where "estimate error" is probably accounting for the lion's share of variance in estimated expected value, and therefore I believe that a proper Bayesian adjustment would correctly assign little value where there is little basis for the estimate, no matter how high the midpoint of the estimate.
Say that you've come to believe - based on life experience - in a "prior distribution" for the value of your actions, with a mean of zero and a standard deviation of 1. (The unit type you use to value your actions is irrelevant to the point I'm making; so in this case the units I'm using are simply standard deviations based on your prior distribution for the value of your actions). Now say that someone estimates that action A (e.g., giving in to the mugger's demands) has an expected value of X (same units) - but that the estimate itself is so rough that the right expected value could easily be 0 or 2X. More specifically, say that the error in the expected value estimate has a standard deviation of X.
An EEV approach to this situation might say, "Even if there's a 99.99% chance that the estimate is completely wrong and that the value of Action A is 0, there's still an 0.01% probability that Action A has a value of X. Thus, overall Action A has an expected value of at least 0.0001X; the greater X is, the greater this value is, and if X is great enough then, then you should take Action A unless you're willing to bet at enormous odds that the framework is wrong."
However, the same formula discussed above indicates that Action X actually has an expected value - after the Bayesian adjustment - of X/(X^2+1), or just under 1/X. In this framework, the greater X is, the lower the expected value of Action A. This syncs well with my intuitions: if someone threatened to harm one person unless you gave them $10, this ought to carry more weight (because it is more plausible in the face of the "prior" of life experience) than if they threatened to harm 100 people, which in turn ought to carry more weight than if they threatened to harm 3^^^3 people (I'm using 3^^^3 here as a representation of an unimaginably huge number).
The point at which a threat or proposal starts to be called "Pascal's Mugging" can be thought of as the point at which the claimed value of Action A is wildly outside the prior set by life experience (which may cause the feeling that common sense is being violated). If someone claims that giving him/her $10 will accomplish 3^^^3 times as much as a 1-standard-deviation life action from the appropriate reference class, then the actual post-adjustment expected value of Action A will be just under (1/3^^^3) (in standard deviation terms) - only trivially higher than the value of an average action, and likely lower than other actions one could take with the same resources. This is true without applying any particular probability that the person's framework is wrong - it is simply a function of the fact that their estimate has such enormous possible error. An ungrounded estimate making an extravagant claim ought to be more or less discarded in the face of the "prior distribution" of life experience.
Generalizing the Bayesian approach
In the above cases, I've given quantifications of (a) the appropriate prior for cost-effectiveness; (b) the strength/confidence of a given cost-effectiveness estimate. One needs to quantify both (a) and (b) - not just quantify estimated cost-effectiveness - in order to formally make the needed Bayesian adjustment to the initial estimate.
But when it comes to giving, and many other decisions, reasonable quantification of these things usually isn't possible. To have a prior, you need a reference class, and reference classes are debatable.
It's my view that my brain instinctively processes huge amounts of information, coming from many different reference classes, and arrives at a prior; if I attempt to formalize my prior, counting only what I can name and justify, I can worsen the accuracy a lot relative to going with my gut. Of course there is a problem here: going with one's gut can be an excuse for going with what one wants to believe, and a lot of what enters into my gut belief could be irrelevant to proper Bayesian analysis. There is an appeal to formulas, which is that they seem to be susceptible to outsiders' checking them for fairness and consistency.
But when the formulas are too rough, I think the loss of accuracy outweighs the gains to transparency. Rather than using a formula that is checkable but omits a huge amount of information, I'd prefer to state my intuition - without pretense that it is anything but an intuition - and hope that the ensuing discussion provides the needed check on my intuitions.
I can't, therefore, usefully say what I think the appropriate prior estimate of charity cost-effectiveness is. I can, however, describe a couple of approaches to Bayesian adjustments that I oppose, and can describe a few heuristics that I use to determine whether I'm making an appropriate Bayesian adjustment.
Approaches to Bayesian adjustment that I oppose
I have seen some argue along the lines of "I have a very weak (or uninformative) prior, which means I can more or less take rough estimates literally." I think this is a mistake. We do have a lot of information by which to judge what to expect from an action (including a donation), and failure to use all the information we have is a failure to make the appropriate Bayesian adjustment. Even just a sense for the values of the small set of actions you've taken in your life, and observed the consequences of, gives you something to work with as far as an "outside view" and a starting probability distribution for the value of your actions; this distribution probably ought to have high variance, but when dealing with a rough estimate that has very high variance of its own, it may still be quite a meaningful prior.
I have seen some using the EEV framework who can tell that their estimates seem too optimistic, so they make various "downward adjustments," multiplying their EEV by apparently ad hoc figures (1%, 10%, 20%). What isn't clear is whether the size of the adjustment they're making has the correct relationship to (a) the weakness of the estimate itself (b) the strength of the prior (c) distance of the estimate from the prior. An example of how this approach can go astray can be seen in the "Pascal's Mugging" analysis above: assigning one's framework a 99.99% chance of being totally wrong may seem to be amply conservative, but in fact the proper Bayesian adjustment is much larger and leads to a completely different conclusion.
Heuristics I use to address whether I'm making an appropriate prior-based adjustment
Conclusion