Interpreting Quantum Mechanics in Infra-Bayesian Physicalism

Yegreg

This work was inspired by a question by Vanessa Kosoy, who also contributed several of the core ideas, as well as feedback and mentorship.

Abstract

We outline a computationalist interpretation of quantum mechanics, using the framework of infra-Bayesian physicalism. Some epistemic and normative aspects of this interpretation are illuminated by a number of examples and theorems.

1. Introduction

Infra-Bayesian physicalism was introduced as a framework to investigate the relationship between a belief about a joint computational-physical universe and a corresponding belief about which computations are realized in the physical world, in the context of "infra-beliefs". Although the framework is still somewhat tentative and the definitions are not set in stone, it is interesting to explore applications in the case of quantum mechanics.

1.1. Discussion of the results

Quantum mechanics has been notoriously difficult to interpret in a fully satisfactory manner. Investigating the question through the lens of computationalism, and more specifically in the setting of infra-Bayesian physicalism provides a new perspective on some of the questions via its emphasis on formalizing aspects of metaphysics, as well as its focus on a decision-theoretic approach. Naturally, some questions remain, and some new interesting questions are raised by this framework itself.

The toy setup can be described on the high level as follows (with details given in Sections 2 to 4). We have an "agent": in this toy model simply consisting of a policy, and a memory tape to record observations. The agent interacts with a quantum mechanical "environment": performing actions and making observations. We assume the entire agent-environment system evolves unitarily. We'll consider the agent having complete Knightian uncertainty over its own policy, and for each policy the agent's beliefs about the "universe" (the joint agent-environment system) is given by the Born rule for each observable, without any assumption on the correlation between observables (formally given by the free product). We can then use the key construction in infra-Bayesian physicalism — the bridge transform — to answer questions about the agent's corresponding beliefs about what copies of the agent (having made different observations) are instantiated in the given universe.

In light of the falsity of Claims 4.15 and 4.17, we can think of the infra-Bayesian physicalist setup as a form of many-worlds interpretation. However, unlike the traditional many-worlds interpretation, we have a meaningful way of assigning probabilities to (sets of) Everett branches, and Theorem 4.19 shows statistical consistency with the Copenhagen interpretation. In contrast with the Copenhagen interpretation, there is no "collapse", but we do assume a form of the Born rule as a basic ingredient in our setup. Finally, in contrast with the de Broglie–Bohm interpretation, the infra-Bayesian physicalist setup does not privilege particular observables, and is expected to extend naturally to relativistic settings. See also Section 8 for further discussion on properties that are specific to the toy setting and ones that are more inherent to the framework. It is worth pointing out that the author is not an expert in quantum interpretations, so a lot of opportunities are left open for making connections with the existing literature on the topic.

1.2. Outline

In Section 2 we describe the formal setup of a quantum mechanical agent-environment system. In Section 3 we recall some of the central constructions in infra-Bayesian physicalism, then in Section 4 we apply this framework to the agent-environment system. In Sections 4.2 and 4.3 we write down various statements relating quantities arising in the infra-Bayesian physicalist framework to the Copenhagen interpretation of quantum mechanics. While Section 4.2 focuses on "epistemic" statements, Section 4.3 is dedicated to the "normative" aspects. A general theme in both sections is that the stronger, "on the nose" relationships between the interpretations fail, while certain weaker "asymptotic" relationships hold. In Section 5.1 we construct counterexamples to the stronger claims, and in in Sections 6 and 7 we prove the weaker claims relating the interpretations. In Section 8 we discuss which aspects of our setup are for the sake of simplicity in the toy model, and which are properties of the broader theory.

2. Setup

First, we'll describe a standard abstract setup for a simplified agent-environment joint system. We have the following ingredients:

A finite set of possible actions of the agent.
A finite set $O$ of possible observations of the agent. We'll write $E = O \times A$ , the set of observation-action pairs.
For technical reasons it will be convenient to add a symbol $0$ for "blank", and fix a bijection $E_{+} = E ⊔ {0} ≅ Z / N$ preserving $0$ , where $N = | O | \cdot | A | + 1.$ We'll use this bijection to treat $E_{+}$ as an abelian group implicitly.
A Hilbert space $H^{e}$ corresponding to states of the environment.
Fix a finite time horizon^[1] $T \in N$ . A classical state of a cyclic, length $T$ memory tape is a function $τ : Z / T \to E_{+}$ . Let ${Tp}_{T}$ be the set of all classical tape states.
A Hilbert space $H^{g}$ with orthonormal basis $∣ ∣ ψ_{τ}^{g} ⟩$ for $τ \in Tp$ , corresponding to the quantum state of the agent.
For each $a \in A$ a unitary map of the environment $U_{a} : H^{e} \to H^{e}$ , describing the "result of the action".
A projection-valued measure $P$ on $O$ , valued in $H^{e}$ (giving projections $P_{o} : H^{e} \to H^{e}$ for each observation $o \in O$ ).
Let $H = H^{g} \otimes H^{e}$ be the state space of the joint agent-environment system.

Remark 2.1. It would be interesting to consider a setting where the agent is allowed to choose the observation in each step (e.g. have the projection-valued measure $P$ depend on the action taken). For simplicity we'll work with a fixed observation as described above.

Definition 2.2. Let $O^{\leq T} = t \leq T ⨆ t \in N O^{t}$ $E^{\leq T} = t \leq T ⨆ t \in N E^{t}$ be the set of observation histories and observation-action histories respectively, i.e. finite strings of observations (resp. observation-action pairs) up to length $T$ . There's a natural map $obs : E^{\leq T} \to O^{\leq T},$ extracting the string of observations from a string of observation-action pairs. We'll call a function $π : O^{\leq T} \to A$ a policy. For two histories $h_{1}, h_{2}$ (of either type), we'll sometimes write $h_{1} ⊏ h_{2}$ to mean $h_{1}$ is a (not necessarily proper) prefix (i.e. initial substring) of $h_{2}$ .

Remark 2.3. We only consider deterministic policies here. It's not immediately clear how one would generalize Definition 2.7 to randomized policies. In fact, we can always (and is perhaps more principled to) think of our source of randomness for a randomized policy to be included in the environment, so we don't lose out on generality by only considering deterministic policies. For example, if the source of our randomness is a quantum coin flip, then our approach offers a convenient way of modeling this by including the coin as a factor of $H^{e}$ , i.e. part of the environment subsystem.

Definition 2.4. For a tape state $τ : Z / T \to E_{+}$ and an observation-action pair $ε \in E$ , let $mem (τ, ε) : Z / T \to E_{+}$ be the state of the tape after writing the pair $ε$ to the tape, defined by $mem (τ, ε) (n) = {\begin{matrix} τ (n - 1) & n \neq 0 τ (- 1) + ε & n = 0. \end{matrix}$

Remark 2.5. Choosing a group structure on $E_{+}$ is in order to make the map $mem (-, ε) : Tp \to Tp$ invertible, which in turn makes the map $U_{π}^{o}$ in Definition 2.7 unitary.

Definition 2.6. Let the "history extraction" map $hist : Tp \to E^{\leq T}$ be defined by $hist (τ) = (τ (N - 1), \dots, τ (0)) \in E^{N},$ where $0 \leq N \leq T$ is largest such that there's no $0 \leq n < N$ with $τ (n) = 0$ (i.e. so that the $[0, N)$ portion of the tape contains no blanks).

Definition 2.7 (Time evolution of a policy). For each policy $π : O^{\leq T} \to A$ , we define the single time-step unitary evolution operator $U_{π}$ on $H$ as the composite of an "observation" and an "action" operator $U_{π} = U_{A, π} \circ U_{O, π}$ , where $\begin{matrix} U_{O, π} (∣ ∣ ψ_{τ}^{g} ⟩ \otimes P_{o} | ψ^{e} ⟩) & = ∣ ∣ ψ_{mem (τ, (o, a))}^{g} ⟩ \otimes P_{o} | ψ^{e} ⟩ & for all o \in O U_{A, π} (∣ ∣ ψ_{τ}^{g} ⟩ \otimes | ψ^{e} ⟩) & = ∣ ∣ ψ_{τ}^{g} ⟩ \otimes U_{a} | ψ^{e} ⟩ & for a = π (obs (hist (τ))) \end{matrix}$ The time evolution after $t \in N$ time-steps is given by $U_{π}^{t} = U_{π} \circ \dots \circ U_{π}$ , i.e. $U_{π}$ composed with itself $t$ times.

Remark 2.8. As defined above, the first step in the evolution is an observation, so we never use the value of the policy on the empty observation string. In this respect it would be more natural to start with an action instead, but it would make some of the notation and the examples more cumbersome, so we sacrifice a bit of naturality for the sake of simplicity overall.

Lemma 2.9. The operator $U_{π}$ is unitary on $H$ .

Proof. The operator $U_{A, π}$ is clearly unitary since each $U_{a}$ is. We can see that $U_{O, π}$ is unitary as follows. Choose an orthonormal basis $∣ ∣ ψ_{o, i}^{e} ⟩$ of $P_{o} H^{e}$ for each $o \in O$ , so together they form an orthonormal basis for $H^{e}$ (note that the range of $i$ might vary for varying $o$ ). Then $∣ ∣ ψ_{τ}^{g} ⟩ \otimes ∣ ∣ ψ_{o, i}^{e} ⟩$ forms an orthonormal basis for $H$ , and $U_{O, π}$ permutes this basis, hence is unitary. $\begin{matrix} □ \end{matrix}$

3. Prerequisites

We recall some definitions and lemmas within infra-Bayesianism. This is in order to make the current article fairly self-contained, all the relevant notions here were introducted in [IBP], [BIMT] and [LBIMT]. In particular we omit proofs in this section, all the relevant proofs can be found in the articles listed.

3.1. Ultracontributions

First of all, we work with a notion of belief intended to incorporate a form of Knightian uncertainty. Formally, this means that we work with sets of distributions (or rather "contributions" turn out to be a more flexible tool).

Definition 3.1. Given a finite set $X$ , a contribution $μ$ is a non-negative measure on $X$ , such that $μ (X) \leq 1$ . We denote the set of contributions $Δ^{c} X$ . A contribution is a distribution if $μ (X) = 1$ , so we have $Δ X \subset Δ^{c} X$ .

There's a natural order on $Δ^{c} X$ , given by pointwise comparison.

Definition 3.2. We call a subset $A \subset Δ^{c} X$ downward closed if for $μ \in A$ , $ν \leq μ$ implies $ν \in A$ .

As a subspace of $R^{X}$ , the set $Δ^{c} X$ inherits a metric and a convex structure.

Definition 3.3. We call a closed, convex, downward closed subset $Θ \subset Δ^{c} X$ a homogenious ulta-contribution (HUC for short). We denote the set of HUCs by $□ X$ .

We'll work with HUCs as our central formal notion of belief in this article. The exact properties required (closed, convex and downward closed) should be illuminated by Lemma 3.6.

Definition 3.4. Given a HUC $Θ \in □ X$ , and a function $f : X \to [0, 1]$ , we define the expected value $E_{Θ} [f] = max θ \in Θ E_{θ} [f] = max θ \in Θ \sum x \in X θ (x) f (x) .$

Thinking of $f$ as a loss function, this is a worst-case expected value, given Knightian uncertainty over the probabilities.

Remark 3.5. It's worth mentioning that the prefix "infra" originates from the concept of infradistributions, which is the notion corresponding to ultracontributions, in the dual setup of utility functions instead of loss functions. We still often use the term "infra" in phrases such as infra-belief or infra-Bayesianism, but now simply carrying the connotation of a "weaker form" of belief etc., compared to the Bayesian analog.

Lemma 3.6. For $Θ \in □ X$ , the expected value defines a convex, monotone, homogeneous functional $E_{Θ} [-] : [0, 1]^{X} \to [0, 1]$ .

Lemma 3.7. There is a duality $Θ \mapsto E_{Θ}$ , between $□ X$ (i.e. closed, convex, and downward closed subsets of $Δ^{c} X$ ) and convex, monotone, and homogeneous functionals $[0, 1]^{X} \to [0, 1]$ .

For a functional $F : [0, 1]^{X} \to [0, 1]$ , the inverse map in the duality is given by $F \mapsto Θ_{F} = ⋂ f : X \to [0, 1] {θ \in Δ^{c} X : E_{θ} [f] \leq F [f]} .$

3.2. Some constructions

For the current article to be more self-contained, we spell out a few definitions used in this discussion.

Definition 3.8. Given a map of finite sets $f : X \to Y$ , we define the pushforward $f_{*} : Δ^{c} X \to Δ^{c} Y$ to be given by the pushforward measure. We use the same notation to denote the pushforward on HUCs, $f_{*} : □ X \to □ Y$ , given by forward image, that is $f_{*} (Θ) = {f_{*} (θ) \in Δ^{c} Y | θ \in Θ} .$ Equivalently, in terms of the expectation values we have for $g : Y \to [0, 1]$ $E_{f_{*} (Θ)} [g] = E_{Θ} [g \circ f] .$

Definition 3.9. Given a collection of finite sets $X_{i}$ , and HUCs $Θ_{i} \in □ X_{i}$ , we define the free product $⋈ i Θ_{i} \in □ (\prod i X_{i})$ as follows. For a contribution $θ \in Δ^{c} \prod_{i} X_{i}$ we have $θ \in ⋈_{i} Θ_{i}$ if and only if for each $j$ , $({pr}_{j})_{*} (θ) \in Θ_{j} \subset Δ^{c} X_{j},$ where ${pr}_{j} : \prod_{i} X_{i} \to X_{j}$ is projection onto the $i$ th factor.

The free product thus specifies the allowed marginal values, but puts no further restriction on the possible correlations.

Definition 3.10 (Total uncertainty). The state of total (Knightian) uncertainty $⊤_{X} \in □ X$ is defined as $⊤_{X} = Δ^{c} X,$ i.e. the subset of all contributions.

Definition 3.11 (Semidirect product). Given a map $β : X \to □ Y$ , and an element $Θ \in □ X$ , we can define the semidirect product $Θ ⋉ β \in □ (X \times Y)$ . This is easier to write down in terms of the expectation functionals, as follows. For $g : X \times Y \to [0, 1]$ , define $E_{Θ ⋉ β} [g] = E_{Θ} [E_{β (x)} [g (x, -)]] .$ Here $E_{β (x)} [g (x, -)]$ is the function $X \to [0, 1]$ , whose value at $x \in X$ is given by by taking expected value with respect to $β (x) \in □ Y$ of the function $g (x, -) : Y \to [0, 1]$ .

As a subset of $Δ^{c} (X \times Y)$ , $⊤_{X} ⋉ β$ can be understood as the convex hull of the $δ_{x} \times θ$ for all $x \in X$ and all $θ \in β (x) \subset Δ^{c} Y$ . For $Θ ⋉ β$ one needs to further restrict to contributions that project down into $Θ \subset Δ^{c} X$ .

3.3. The bridge transform

The key construction we'll be considering in infra-Bayesian physicalism is the bridge transform. This construction is aimed at answering the question "given a belief about the joint computational-physical universe, what should our corresponding belief be about which computations are realized in the physical universe?".

We'll discuss these notions in a bit more detail, but for now both the physical universe $Φ$ and the computational universe $Γ$ are just assumed to be finite sets.

Definition 3.12. Given $Θ \in □ (Γ \times Φ)$ , the bridge transform of $Θ$ , $Br (Θ) \in □ (Γ \times 2^{Γ} \times Φ)$ is defined as follows (cf. [IBP Definition 1.1]). For a contribution $θ \in Δ^{c} (Γ \times 2^{Γ} \times Φ)$ we have $θ \in Br (Θ)$ if and only if for any $s : Γ \to Γ$ , under the composite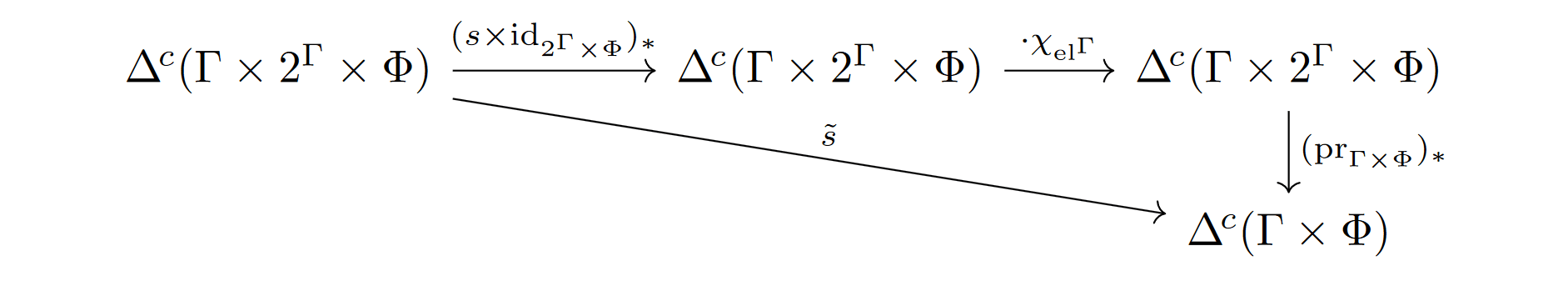 we have $~ s (θ) \in Θ \subset Δ^{c} (Γ \times Φ)$ .

Remark 3.13. The use of all endomorphism $s : Γ \to Γ$ in Definition 3.12, although concise, doesn't feel fully principled as of now. We would typically think of the computational universe $Γ$ as the set of all possible assignments of outputs to programs, i.e. $Γ = Σ^{R}$ , for a certain output alphabet $Σ$ , and a set of programs $R$ (see Definition 4.1). In this context, $Γ^{Γ}$ feels somewhat unnatural. That being said, in the current discussion we mainly use the fact that $Γ^{Γ}$ acts transivitely on $Γ$ , so it's possible that these results would survive in some form under a modified definition of the bridge transform.

For easy reference, we spell out [IBP Proposition 2.10]:

Lemma 3.14 (Refinement). Given a mapping between physical universes $f : Φ_{1} \to Φ_{2}$ , we ha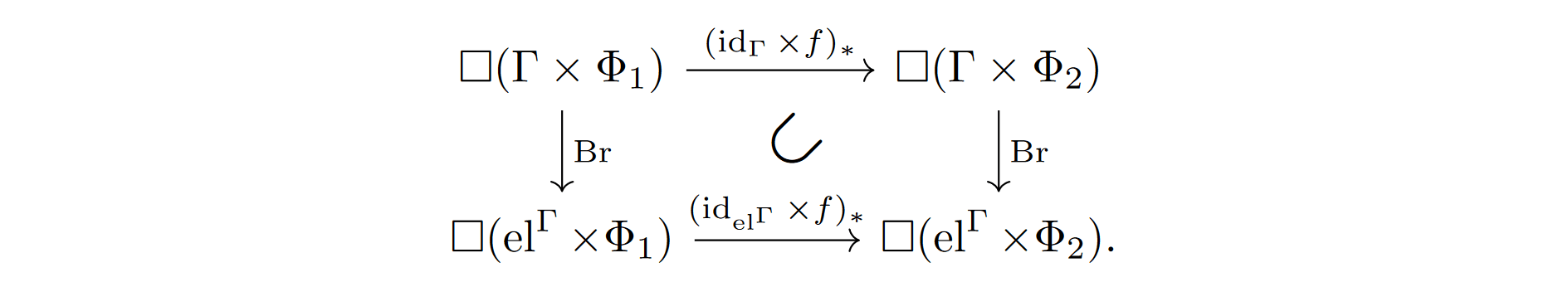ve That is, for a belief $Θ \in □ (Φ_{1} \times Γ)$ we have $({id}_{{el}^{Γ}} \times f)_{*} (Br (Θ)) \subset Br (({id}_{Γ} \times f)_{*} (Θ)) .$

4. An infra-Bayesian physicalist interpretation

We'll work with a certain specialized setup of [IBP].

Definition 4.1. Let the set of "programs" $R = O^{\leq T}$ , the "output alphabet" $Σ = A$ , and the set of "computational universe states" $Γ = Σ^{R} = A^{O^{\leq T}}$ be the set of policies up to time horizon $T$ . We'll write ${el}^{Γ} = {(π, α) \in Γ \times 2^{Γ} : π \in α} .$

Definition 4.2. Let a "universal observable" $B$ be a triple $(V_{B}, Q_{B}, t_{B}),$ where $V_{B}$ is a finite set (of "observation outcomes"), $Q_{B}$ is a projection-valued measure on $V_{B}$ , valued in $H$ (giving projections $Q_{B} (v) : H \to H$ for each $v \in V_{B}$ ), and an "observation time" $t_{B} \in N_{< T}$ . Let $U$ be the set of all universal observables, up to the natural notion of equivalence.

Remark: We use the term "universal observable" here to distinguish between observables of the "universe" (i.e. the joint agent-environment system) from the observations of the environment by the agent.

Definition 4.3 (Initial state). Fix a normalized (norm $1$ ) initial state $∣ ∣ ψ_{0}^{e} ⟩ \in H^{e}$ of the environment, and let $∣ ∣ ψ_{0}^{g} ⟩$ be the state of the agent corresponding to an empty memory tape, i.e. $τ : Z / T \to E$ given by $τ (n) = 0$ for all $n$ . Let $| ψ_{0} ⟩ = ∣ ∣ ψ_{0}^{g} ⟩ \otimes ∣ ∣ ψ_{0}^{e} ⟩ \in H$ be the initial state of the joint system.

Definition 4.4. For a policy $π \in Γ$ , let the marginal distribution of the universal observable $B$ be defined according to the Born rule: $β_{B} (v | π) = ∥ Q_{B} (v) U_{π}^{t_{B}} | ψ_{0} ⟩ ∥^{2} .$ I.e. the norm square of the vector obtained by evolving the universe following policy $π$ for $t_{B}$ time-steps from the initial state, and then projecting onto the observation subspace corresponding to the universal observation $v \in V_{B}$ . So $β_{B} (- | π) \in Δ V_{B} .$

Definition 4.5. Let $Φ_{U} = \prod B \in U V_{B}$ be the set of "all possible states of the universe" (more precisely the set of all possible outcomes of all observations on the joint agent-environment system). More generally, define $Φ_{S}$ analogously for any subset $S \subset U$ .

Definition 4.6. For a finite subset $F \subset U$ , let $β_{F} (π) = ⋈ B \in F β_{B} (- | π) \in □ Φ_{F}$ be the free product of the $β_{B}$ , as defined in Definition 3.9. For varying $π$ this defines an ultrakernel $β_{F} : Γ \to □ Φ_{F},$ and the associated semidirect product $Θ_{F} = ⊤_{Γ} ⋉ β_{F} \in □ (Γ \times Φ_{F}) .$ Taking the bridge transform and projecting out the physical factor $Φ_{F}$ : $□ (Γ \times Φ_{F}) Br - \to □ (Γ \times 2^{Γ} \times Φ_{F}) {pr}_{*} - - \to □ (Γ \times 2^{Γ}),$ we get $Θ_{F}^{*} = {pr}_{*} (Br (Θ_{F})) \in □ (Γ \times 2^{Γ}) .$

If $F_{1} \subset F_{2} \subset U$ , we have a natural "refinement" map $p : Φ_{F_{2}} \to Φ_{F_{1}}$ , given by projecting out the additional factors in $Φ_{F_{2}}$ . By Lemma 3.14, we have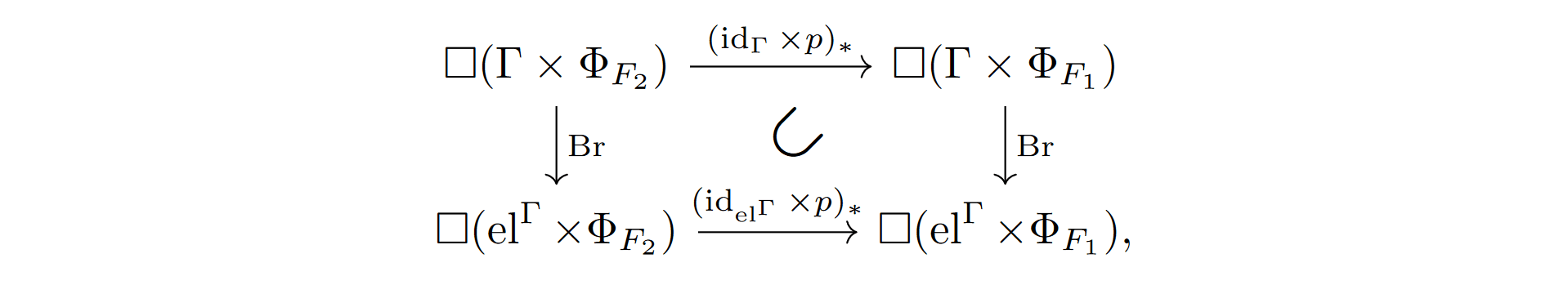 Diagram for refinement so $Θ_{F_{2}}^{*} \subset Θ_{F_{1}}^{*}$ . Inspired by this, we have the following.

Definition 4.7. Let $Θ_{U}^{*} = ⋂ F \subset U Θ_{F}^{*},$ where the intersection is over all finite subsets of $U$ .

4.1. Copenhagen interpretation

Definition 4.8. Let $h \in E^{\leq T}$ be an observation-action history, and denote by $Q_{h} : H \to H$ the projection corresponding to the proposition "the memory tape recorded history $h$ ". More precisely $Q_{h} = Q_{h}^{g} \otimes {id}_{H^{e}}$ , where $Q_{h}^{g} ∣ ∣ ψ_{τ}^{g} ⟩ = {\begin{matrix} ∣ ∣ ψ_{τ}^{g} ⟩ & if hist (τ) = h 0 & otherwise. \end{matrix}$

Definition 4.9. Given a sequence of observation-action pairs $h \in E^{n}$ , let $h_{\leq m} \in E^{\leq m}$ denote the truncated history (i.e. the image under projecting out the last $n - m$ components of $E^{n}$ if $n > m$ , and $h$ itself if $n \leq m$ ).

In the Copenhagen interpretation the "universe" (i.e. the joint system of the agent and the environment) collapses after each observation of the agent.

Definition 4.10. Given a policy $π : O^{\leq T} \to A$ , the initial state $| ψ_{0} ⟩ \in H$ , and a sequence of observation-action pairs $h \in E^{n}$ , we can define $| ψ_{t} ⟩ = Q_{h_{\leq t}} U_{π} | ψ_{t - 1} ⟩$ for $t > 0$ recursively. Then according to the Copenhagen interpretation, the probability of observing $h$ is $Cop (h | π) = ∥ | ψ_{n} ⟩ ∥^{2} .$

Lemma 4.11. Collapsing at each step is the same as collapsing at the end, that is $| ψ_{t} ⟩ = Q_{h_{\leq t}} U_{π}^{t} | ψ_{0} ⟩ .$

Proof. The claim is true for $t = 0, 1$ by definition. Assume it's true for $t - 1$ , so $| ψ_{t - 1} ⟩ = Q_{h_{\leq t - 1}} U_{π}^{t - 1} | ψ_{0} ⟩ .$ Let's write $U_{π}^{t - 1} | ψ_{0} ⟩ = \sum τ \in Tp ∣ ∣ ψ_{τ}^{g} ⟩ \otimes | φ_{τ}^{e} ⟩,$ so $| ψ_{t - 1} ⟩ = \sum \begin{matrix} τ \in Tp hist (τ) = h_{\leq t - 1} \end{matrix} ∣ ∣ ψ_{τ}^{g} ⟩ \otimes | φ_{τ}^{e} ⟩ .$ Then if $a = π (obs (h_{\leq t - 1})) \in A$ , we have $| ψ_{t} ⟩ = \sum \begin{matrix} τ \in Tp hist (τ) = h_{\leq t} \end{matrix} ∣ ∣ ψ_{τ}^{g} ⟩ \otimes P_{h (t)} U_{a} | φ_{τ}^{e} ⟩,$ while $U_{π}^{t} | ψ_{0} ⟩ = \sum \begin{matrix} τ \in Tp o \in O \end{matrix} ∣ ∣ ψ_{mem (τ, (o, a))}^{g} ⟩ \otimes P_{o} U_{π (hist (τ))} | φ_{τ}^{e} ⟩ .$ Now $Q_{h_{\leq t}} ∣ ∣ ψ_{mem (τ, (o, a))}^{g} ⟩ = 0$ unless $(o, a) = h (t)$ and $hist (τ) = h_{\leq t - 1}$ , hence $Q_{h_{\leq t}} U_{π}^{t} | ψ_{0} ⟩ = | ψ_{t} ⟩$ as claimed. $\begin{matrix} □ \end{matrix}$

4.2. Relating the two interpretations

Since $Θ_{U}^{*} \in □ {el}^{Γ}$ , we can take expectations of functions $f : {el}^{Γ} \to [0, 1]$ , in particular indicator functions $χ_{q}$ for $q \subset {el}^{Γ}$ .

Definition 4.12. For a policy $π \in Γ$ , and a tuple of observations $h \in O^{n}$ , define $α_{h | π} = {γ \in Γ | γ (h) = π (h)} \subset Γ,$ and let $q_{h | π} = {(π, α) \in {el}^{Γ} | α \subset α_{h | π}} \subset {el}^{Γ} .$

Remark 4.13. In what follows we'll assume $| A | > 1$ . This assures that the set of policies is richer than the set of histories (i.e. $| Γ | > | O^{\leq T} |)$ . Much of the following fails in the degenerate case $| A | = 1$ .

When considering the infra-Bayesian physicalist interpretation of a quantum event $h$ , we'll consider the expected value $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})] .$ As defined in Definition 4.6, $Θ_{U}$ can be thought of as the infra-belief $⊤_{Γ} ⋉ β_{U} \in □ (Γ \times Φ_{U}),$ which is a joint belief over the computational-physical world, with complete Knightian uncertainty over the policy of the agent (as a representation of "free will"), and for each policy the corresponding belief about the physical world is as given by the unitary quantum evolution of the agent-environment system under the given policy. The bridge transform $Θ_{U}^{*} \in □ {el}^{Γ}$ of $Θ_{U}$ then packages the relevant beliefs about which computational facts are manifest in the physical world. The subset $α_{h | π}$ corresponds to the proposition "the policy outputs action $a = π (h)$ upon observing $h$ ", and hence $q_{h | π}$ corresponds to the belief "the physical world witnesses the output of the policy on $h$ to be $a = π (h)$ (which is to say there's a version of the agent instantiated in the physical world that observed history $h$ , and acted $a$ )". We'll be investigating various claims about the quantity $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})],$ which is the ultraprobability (i.e. the highest probability for the given Knightian uncertainty) of the agent following policy $π$ and $h$ not being observed (i.e. no agent being instantiated acting on history $h$ ).

Remark 4.14. It might at first seem more natural to consider the complement instead, that is $χ_{π} χ_{q_{h | π}}$ , which corresponds to the agent following policy $π$ , and history $h$ being observed. However, it turns out that $E_{Θ_{U}^{*}} [χ_{π} χ_{q_{h | π}}] = 1$ always. This can be understood intuitively via refinement (see Lemma 3.14): we can always extend our model of the physical world to include a copy of the agent instantiated on history $h$ , so the highest probability of $h$ being observed will be $1$ . This is also related to the monotonicity principle discussed in [IBP]. Thus although at first glance this might seem less natural, in our setup it's more meaningful to study the ultraprobability of the complement, i.e. of $h$ not being observed. Note that since we're working with convex instead of linear expectation functionals (see Lemma 3.7), the complementary ultraprobabilities will typically sum to something greater than one.

We first state Claims 4.15 and 4.17 relating the IBP and Copenhagen interpretations "on the nose", which both turn out to be false in general. Then we state the weaker Theorem 4.19, which is true, and establishes a form of asymptotic relationship between the two interpretations.

Claim 4.15. The two interpretations agree on the probability that a certain history is not realized given a policy. That is, $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})] = 1 - Cop (h | π) .$

This claim turns out to be false in general, and we give a counterexample in Counterexample 5.3. Note, however, that the claim seems to be true in the limit with many actions (i.e. $| A | \to \infty$ ), which would warrant further study. Now consider the following definition concerning two copies of the agent being instantiated.

Definition 4.18. For a policy $π \in Γ$ , and two tuples of observations $h_{1}, h_{2} \in O^{n}$ , define $α_{h_{1}, h_{2} | π} = {γ \in Γ | γ (h_{i}) = π (h_{i}) for i = 1, 2} \subset Γ,$ and let $q_{h_{1}, h_{2} | π} = {(π, α) \in {el}^{Γ} | α \subset α_{h_{1}, h_{2} | π}} \subset {el}^{Γ} .$

Claim 4.17. There is only one copy of the agent (i.e. the agent is not instantiated on multiple histories, there are no "many worlds"). That is, if neither of $h_{1}, h_{2} \in O^{n}$ is a prefix of the other, then $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h_{1}, h_{2} | π}})] = 1.$

This claim is the relative counterpart of Claims 4.15 and fails as well in general (see Counterexample 5.5). Again, however, this claim might hold in the $| A | \to \infty$ limit.

Definition 4.18. An event is a subset of histories $E \subset O^{T}$ . We define the corresponding $q_{E | π} = ⋃ h \in E q_{h | π} \subset {el}^{Γ},$ and $Cop (E | π) = \sum h \in E Cop (h | π) .$

Theorem 4.19. The ultraprobability of an agent not being instantiated on a certain event can be bounded via functions of the (Copenhagen) probability of the event. More precisely, $1 - \sqrt{(2 - Cop (E | π)) Cop (E | π)} \leq E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{E | π}})] \leq 1 - Cop (E | π) .$

Proof. We prove the upper bound in Section 6.1 and the lower bound in Section 6.2. $\begin{matrix} □ \end{matrix}$

Due to the failure of Claims 4.15 and 4.17, we can think of the infra-Bayesian physicalist setup as a form of many-worlds interpretation. However, since $\sqrt{(2 - Cop (E | π)) Cop (E | π)} \to 0 as Cop (E | π) \to 0,$ the above Theorem 4.19 shows statistical consistency with the Copenhagen interpretation in the sense that observations that are unlikely according to the Born rule have close to $1$ ultraprobability of not being instantiated (while very likely observations have close to $0$ ultraprobability of uninstantiation).

Remark 4.20. For simplicity we assumed $E$ only contains entire histories (i.e. ones of maximal length $T$ ). It's easy to modify the definitions to account for partial histories. The inequalities in Theorem 4.19 remain true even if $E$ includes partial histories, and the proofs are easy to adjust. We avoid doing this here in order to keep the notation cleaner. However, it's worth noting some important points here. For a partial history $h$ , let $H \subset O^{T}$ be the set of all completions of $h$ , i.e. $H = {~ h \in O^{T} : h ⊏ ~ h} .$ Then we have $Cop (h | π) = Cop (H | π) = \sum ~ h \in H Cop (~ h | π) .$ On the other hand, $q_{h | π} \neq q_{H | π} = ⋃ ~ h \in H q_{~ h | π},$ so there is an important difference here between the two interpretations, which would warrant further discussion. In particular, under the infra-Bayesian physicalist interpretation it can happen that $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{H | π}})] > E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})]$ for a partial history $h$ and its set of completions $H$ . This could be loosely interpreted as Everett branches "disappearing", as the ultraprobability of an agent not being instantiated on the partial history $h$ is less than that of the agent not being instantiated on any completion of that history.

4.3. Decision theory

To shed more light on the way the infra-Bayesian physicalist interpretation functions, it is interesting to consider the decision theory of the framework, along with the epistemic considerations above.

Definition 4.21. Consider a loss function $L : D \to R_{\geq 0},$ where $D = E^{T}$ is the set of destinies. We can then construct the physicalized loss function (cf. [IBP Definition 3.1]) $L^{phys} : {el}^{Γ} \to R_{\geq 0},$ given by $L^{phys} (γ, α) = min h \in X_{α} max \begin{matrix} d \in D h ⊏ d \end{matrix} L (d),$ where $X_{α}$ is the set of histories witnessed by $α$ , that is $X_{α} = {h \in E^{\leq T} | \forall g a ⊏ h, \forall ~ γ \in α : ~ γ (obs (g)) = a} .$ Note that in our simplified context, $L^{phys} (γ, α)$ doesn't depend on $γ$ .

Definition 4.22. We can define the worst-case expected physicalized loss associated to a policy $π$ by $L^{IBP} (π) = E_{Θ_{U}^{*}} [χ_{π} \cdot L^{phys}] .$ Under the Copenhagen model, we would instead simply consider $L^{Cop} (π) = E_{Cop} [L | π] = \sum d \in D Cop (d | π) L (d) .$

Remark 4.23. Given a policy $π \in Γ$ , we can consider the set of "fair" counterfactuals (cf. [IBP Definition 1.5]) $\begin{matrix} C_{fair}^{π} = {(γ, α) \in {el}^{Γ} | & \forall h \in O^{\leq T} : (\forall ~ γ \in α, \forall ~ h ⊏ h : ~ γ (~ h) = γ (~ h)) ⟹ γ (h) = π (h)}, \end{matrix}$ i.e. where if $α$ witnesses the history $h$ , then $γ$ agrees with $π$ on that history. This definition is in contrast with the "naive" counterfactuals we considered above (when writing $χ_{π}$ ): $C_{naive}^{π} = {(γ, α) \in {el}^{Γ} | γ = π} .$ In Definition 4.22 above, and generally whenever we use $χ_{π}$ , we could have used the indicator function of $C_{fair}^{π}$ instead. The choice of counterfactuals affects the various expected values, however, all of the theorems in this article remain true (and Claims 4.15 and 4.17 remain false) for both naive and fair counterfactuals. We thus work with naive counterfactuals for the sake of simplicity.

Similarly to Section 4.2, the "on the nose" claim relating the two interpretations fails, but we have an asymptotic relationship which holds.

Claim 4.24. The two interpretations agree on the loss of any policy: $L^{IBP} (π) = L^{Cop} (π) .$

Again, this turns out to be false, and we give a simple counterexample in Counterexample 5.6.

To allow discussing the asymptotic behavior, assume now that we incur a loss at each timestep, given by $ℓ : E = O \times A \to R_{\geq 0},$ and we consider the total loss $L = T \sum t = 1 ℓ_{t} : D \to R_{\geq 0} .$ We might hope that we could have at least the following.

Claim 4.25. The two interpretations agree on the loss of any policy asymptotically: $L^{IBP} (π) \sim L^{Cop} (π),$ i.e. the difference is bounded sublinearly in $T$ .

This claim is still false in general for essentially the same reason as Claim 4.24 since certain policies might involve a one-off step that then affect the entire asymptotic loss. We give a detailed explanation in Counterexample 5.7. We do however have the following.

Theorem 4.26. If the resulting MDP is communicating (see Definition 7.8), then for any policy $π$ we have $L^{Cop} (π^{*}) - o (T) \leq L^{IBP} (π) \leq L^{Cop} (π),$ where $π^{*}$ is a Copenhagen-optimal policy. In particular, optimal losses for the IBP and Copenhagen frameworks agree asymptotically.

Proof. See Theorem 7.1 for the upper bound and Theorem 7.21 for the lower bound. $\begin{matrix} □ \end{matrix}$

5. Examples

We'll look at a few concrete examples in detail, firstly to gain some insight into how Claims 4.15 and 4.17 fail in general, and secondly to see how our framework operates in the famously puzzling Wigner's friend scenario.

5.1. Counterexamples

We'll construct simple counterexamples to Claims 4.15 and 4.17 in the smallest non-degenerate case, i.e. when $| O | = 2$ and $| A | = 2$ , and $T = 1$ . Let $O = {o_{0}, o_{1}}$ and $A = {a_{0}, a_{1}}$ . There are four policies in this case (ignoring the value of the policies on the empty input, which is irrelevant in our setting, see Remark 2.8), which we'll abbreviate as $π_{00}, π_{01}, π_{10}, π_{11}$ , where $\begin{matrix} π_{i j} (o_{0}) & = a_{i} π_{i j} (o_{1}) & = a_{j} . \end{matrix}$ Assume $h = o_{0}$ , and $π = π_{00}$ , so $α_{h | π} = {π_{00}, π_{01}}$ .

Recall [IBP Lemma 1]:

Lemma 5.1. For $ρ \in Δ^{c} {el}^{Γ} \times Φ$ , we have $ρ \in Br (Θ)$ if and only if for each $s : Γ \to Γ$ and $g : Γ \times Φ \to [0, 1]$ $E_{ρ} [~ g] \leq E_{Θ} [g],$ where $~ g : {el}^{Γ} \times Φ \to [0, 1]$ is given by $γ, α, x \mapsto χ_{s (γ) \in α} \cdot g (s (γ), x)$ .

Lemma 5.2. Let $β : Γ \to Δ Φ$ be a kernel, $Θ = ⊤_{Γ} ⋉ β$ , and $Θ^{*} = {pr}_{*} (Br (Θ))$ as above. Then $E_{Θ^{*}} [χ_{π} (1 - χ_{q_{h | π}})] = E_{(β (π_{10}) + β (π_{11})) \land β (π_{00})} [1] .$

Proof. To obtain a lower bound (although we'll only use the upper bound for the counterexample), define the contribution $ρ \in Δ^{c} ({el}^{Γ} \times Φ)$ by $ρ = δ_{π_{00}, {π_{00}, π_{10}}} \times ϕ_{10} + δ_{π_{00}, {π_{00}, π_{11}}} \times ϕ_{11},$ where $ϕ_{10}, ϕ_{11} \in Δ^{c} Φ$ are such that $ϕ_{10} \leq β (π_{10}),$ $ϕ_{11} \leq β (π_{11}),$ and $ϕ_{10} + ϕ_{11} = (β (π_{10}) + β (π_{11})) \land β (π_{00}) .$ One possible such choice is $ϕ_{10} = β (π_{10}) \land β (π_{00})$ $ϕ_{11} = β (π_{11}) \land (β (π_{00}) - ϕ_{10}) .$ Then it's easy to verify that $ρ \in Br (Θ)$ , and $E_{ρ} [χ_{π} (1 - χ_{q_{h | π}})] = E_{(β (π_{10}) + β (π_{11})) \land β (π_{00})} [1] .$ To obtain an upper bound, fix $x_{0} \in Φ$ , and use Lemma 5.1 for constant $s = π_{00}$ , and $g (γ, x) = χ_{γ = π_{00}} \cdot χ_{x = x_{0}}$ . We have $~ g (γ, α, x) = χ_{π_{00} \in α} \cdot g (π_{00}, x) = χ_{π_{00} \in α} \cdot χ_{x = x_{0}},$ and so $\begin{matrix} E_{ρ} [χ_{π_{00} \in α} \cdot χ_{x = x_{0}}] = E_{ρ} [~ g] \leq E_{Θ} [χ_{γ = π_{00}} \cdot χ_{x = x_{0}}] = E_{β (π_{00})} [χ_{x = x_{0}}] . \\ (1) \end{matrix}$ Analogously for $π_{10}$ and $π_{11}$ we get $\begin{matrix} E_{ρ} [χ_{π_{10} \in α} \cdot χ_{x = x_{0}}] \leq E_{Θ} [χ_{γ = π_{10}} \cdot χ_{x = x_{0}}] = E_{β (π_{10})} [χ_{x = x_{0}}], \\ (2) \end{matrix}$ and $\begin{matrix} E_{ρ} [χ_{π_{11} \in α} \cdot χ_{x = x_{0}}] \leq E_{Θ} [χ_{γ = π_{11}} \cdot χ_{x = x_{0}}] = E_{β (π_{11})} [χ_{x = x_{0}}] . \\ (3) \end{matrix}$

Now, $χ_{π} (1 - χ_{q_{h | π}}) χ_{x = x_{0}} \leq χ_{π_{00} \in α} \cdot χ_{x = x_{0}},$ so by $(1)$ we get $\begin{matrix} E_{ρ} [χ_{π} (1 - χ_{q_{h | π}}) χ_{x = x_{0}}] \leq E_{β (π_{00})} [χ_{x = x_{0}}] . \\ (4) \end{matrix}$

We also have $1 - χ_{q_{h | π}} \leq χ_{π_{10} \in α} + χ_{π_{11} \in α}$ , since $π_{10} \notin α$ and $π_{11} \notin α$ together would imply $α \subset α_{h | π_{00}}$ . Thus $χ_{π} (1 - χ_{q_{h | π}}) χ_{x = x_{0}} \leq (χ_{π_{10} \in α} + χ_{π_{11} \in α}) \cdot χ_{x = x_{0}},$ so adding $(2)$ and $(3)$ , we obtain $\begin{matrix} E_{ρ} [χ_{π} (1 - χ_{q_{h | π}}) χ_{x = x_{0}}] \leq E_{β (π_{10}) + β (π_{11})} [χ_{x = x_{0}}] . \\ (5) \end{matrix}$ Now, since both $(4)$ and $(5)$ hold, we get $E_{ρ} [χ_{π} (1 - χ_{q_{h | π}}) χ_{x = x_{0}}] \leq E_{(β (π_{10}) + β (π_{11})) \land β (π_{00})} [χ_{x = x_{0}}] .$ Finally, summing over $x_{0} \in Φ$ we have the required upper bound $E_{Θ^{*}} [χ_{π} (1 - χ_{q_{h | π}})] = E_{(β (π_{10}) + β (π_{11})) \land β (π_{00})} [1] .$ $\begin{matrix} □ \end{matrix}$

Counterexample 5.3. Let $H^{e}$ be a qubit state space, and $∣ ∣ ψ_{0}^{e} ⟩ = | + ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩) .$ Let $U_{a_{0}} = U_{a_{1}} = {id}_{H^{e}}$ . Let the observation $P$ correspond to measuring the qubit, so $P_{o_{0}}, P_{o_{1}}$ are projections onto $| 0 ⟩$ and $| 1 ⟩$ respectively. Then Claim 4.15 fails in this setup.

Proof. We have $| ψ_{0} ⟩ = ∣ ∣ ψ_{0}^{g} ⟩ \otimes ∣ ∣ ψ_{0}^{e} ⟩ = | 0 ⟩ \otimes \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩),$ and so $U_{π_{00}} | ψ_{0} ⟩ = \frac{1}{\sqrt{2}} (| o_{0} a_{0} ⟩ \otimes | 0 ⟩ + | o_{1} a_{0} ⟩ \otimes | 1 ⟩),$ $U_{π_{10}} | ψ_{0} ⟩ = \frac{1}{\sqrt{2}} (| o_{0} a_{1} ⟩ \otimes | 0 ⟩ + | o_{1} a_{0} ⟩ \otimes | 1 ⟩),$ $U_{π_{11}} | ψ_{0} ⟩ = \frac{1}{\sqrt{2}} (| o_{0} a_{1} ⟩ \otimes | 0 ⟩ + | o_{1} a_{1} ⟩ \otimes | 1 ⟩) .$ Now consider the universal observable $B$ which is measurement along the vector $| v ⟩$ and its complement, where $| v ⟩ = \frac{1}{2 \sqrt{3}} (3 | o_{0} a_{0} ⟩ \otimes | 0 ⟩ + | o_{1} a_{0} ⟩ \otimes | 1 ⟩ - | o_{0} a_{1} ⟩ \otimes | 0 ⟩ + | o_{1} a_{1} ⟩ \otimes | 1 ⟩)$ I.e. we have $V_{B} = {v, v^{⊥}}$ , and $Q_{B} (v) = P_{v},$ $Q_{B} (v^{⊥}) = P_{v^{⊥}},$ where $P_{v}$ , $P_{v^{⊥}}$ are projections in $H = H^{g} \otimes H^{e}$ onto $| v ⟩$ and its ortho-complement respectively. Then we have the following values for $β_{B}$ for the various policies:

	$π_{00}$	$π_{10}$	$π_{11}$
$β_{B} (v)$	2/3	0	0
$β_{B} (v^{⊥})$	1/3	1	1

This can be seen by noticing that $| v ⟩$ is perpendicular to both $U_{π_{10}} | ψ_{0} ⟩$ and $U_{π_{11}} | ψ_{0} ⟩$ , while $⟨ v ∣ ∣ U_{π_{00}} ψ_{0} ⟩ = \frac{2}{\sqrt{6}}$ , so $β_{B} (v | π_{00}) = | ⟨ v ∣ ∣ U_{π_{00}} ψ_{0} ⟩ |^{2} = \frac{2}{3} .$ This means that for this $B$ we have $(β_{B} (π_{10}) + β_{B} (π_{11})) \land β_{B} (π_{00}) [1] = 1 / 3.$ If $F_{B} = {B}$ , by Lemma 5.2 we have $E_{Θ_{F_{B}}^{*}} [χ_{π} (1 - χ_{q_{h | π}})] = E_{(β_{B} (π_{10}) + β_{B} (π_{11})) \land β_{B} (π_{00})} [1] = 1 / 3.$ Now, by definition $Θ_{U}^{*} \subset Θ_{F_{B}}^{*}$ , so we also have $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})] \leq 1 / 3 < 1 - Cop (h | π) = \frac{1}{2} .$ $\begin{matrix} □ \end{matrix}$

Although we won't need the exact value here, we remark to the interested reader that in the above setup of Counterexample 5.3, the ultraprobability attains the lower bound of Theorem 4.19, that is $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{h | π}})] = 1 - \sqrt{3 / 4} \approx 0.134.$

We can extend the above counterexample to apply to Claim 4.17, via the following.

Lemma 5.4. Let $β : Γ \to Δ Φ$ be a kernel, $Θ = ⊤_{Γ} ⋉ β$ , and $Θ^{*} = {pr}_{*} (Br (Θ))$ as above. Then for $h_{1} = o_{0}$ , $h_{2} = o_{1}$ , $E_{Θ^{*}} [χ_{π} (1 - χ_{q_{h_{1}, h_{2} | π}})] = E_{(β (π_{10}) + β (π_{01}) + β (π_{11})) \land β (π_{00})} [1] .$

Proof. Analogous to Lemma 5.2. $\begin{matrix} □ \end{matrix}$

Counterexample 5.5. In the setup of Counterexample 5.3, Claim 4.17 fails too, that is $E_{Θ^{*}} [χ_{π} (1 - χ_{q_{h_{1}, h_{2} | π}})] < 1.$

Proof. Consider projecting onto the three vectors $| v_{1} ⟩ = U_{π_{00}} | ψ_{0} ⟩ = \frac{1}{\sqrt{2}} (| o_{0} a_{0} ⟩ \otimes | 0 ⟩ + | o_{1} a_{0} ⟩ \otimes | 1 ⟩),$ $| v_{2} ⟩ = U_{π_{11}} | ψ_{0} ⟩ = \frac{1}{\sqrt{2}} (| o_{0} a_{1} ⟩ \otimes | 0 ⟩ + | o_{1} a_{1} ⟩ \otimes | 1 ⟩),$ and $\begin{matrix} | v_{3} ⟩ = \frac{1}{\sqrt{2}} (U_{π_{01}} | ψ_{0} ⟩ - U_{π_{10}} | ψ_{0} ⟩) = \frac{1}{2} (| o_{0} a_{0} ⟩ \otimes | 0 ⟩ - | o_{1} a_{0} ⟩ \otimes | 1 ⟩ - | o_{0} a_{1} ⟩ \otimes | 0 ⟩ + | o_{1} a_{1} ⟩ \otimes | 1 ⟩) . \end{matrix}$ Then the corresponding probabilities are

	$π_{00}$	$π_{01}$	$π_{10}$	$π_{11}$
$β_{B} (v_{1})$	1	1/4	1/4	0
$β_{B} (v_{2})$	0	1/2	1/2	0
$β_{B} (v_{3})$	0	1/4	1/4	1

So we have $E_{(β_{B} (π_{10}) + β_{B} (π_{01}) + β_{B} (π_{11})) \land β_{B} (π_{00})} [1] = 1 / 2 < 1.$ Then again, by refinement, this implies that $E_{Θ^{*}} [χ_{π} (1 - χ_{q_{h_{1}, h_{2} | π}})] \leq 1 / 2 < 1$ as well. $\begin{matrix} □ \end{matrix}$

Counterexample 5.6. Claim 4.24 fails in the setup of Counterexample 5.3, with loss given by $ℓ : O \times A \to R_{\geq 0},$ $ℓ (o, a) = {\begin{matrix} 0 if o = o_{0} 1 if o = o_{1} . \end{matrix}$

Proof. In this case $L^{phys} (γ, α) = {\begin{matrix} 0 if \forall ~ γ \in α : ~ γ (o_{0}) = γ (o_{0}) 1 otherwise. \end{matrix}$ Notice that for this $L^{phys}$ we actually have $χ_{π} \cdot L^{phys} = χ_{π} (1 - χ_{q_{o_{0} | π}}),$ so by the considerations in Counterexample 5.3, we also have (for any policy $π$ ) $L^{IBP} (π) \leq 1 / 3 < 1 / 2 = L^{Cop} (π),$ showing failure of Claim 4.24. $\begin{matrix} □ \end{matrix}$

Counterexample 5.7. The setup of Counterexample 5.6, run over time horizon $T$ instead of just a single timestep shows the failure of the asymptotic claim Claim 4.25 in general.

Proof. The point is that in this setup the entire loss is determined by the outcome of the first observation: if we observe $o_{0}$ , we'll incur $0$ loss during the entire time, while if we observe $o_{1}$ first, we're "stuck" in that state, and hence incur a total loss equal to $T$ . Due to this, we have $L^{IBP} (π) \leq \frac{T}{3} ⋦ \frac{T}{2} = L^{Cop} (π),$ for any policy $π$ . $\begin{matrix} □ \end{matrix}$

Note that in the above setup, we get "stuck" in the states after the initial observation because the MDP itself is not communicating. However, even for communicating MDPs (for example if we choose $U_{a_{1}}$ to be a rotation by $π / 4$ ) certain policies will get stuck (for example the policy that always chooses $a_{0}$ corresponding to $U_{a_{0}} = id$ ). So we see this behavior whenever the asymptotic loss is dependent on a few initial steps. On the other hand, for example if $π$ is a stationary policy, and the resulting Markov chain is irreducible, then we can obtain a concentration bound on the loss (e.g. via the central limit theorem, [Dur96^[2], 5.6.6.]), and use an argument similar to Theorem 7.21 to show that $L^{IBP}$ and $L^{Cop}$ indeed agree asymptotically under such assumptions.

5.2. Wigner's friend

We'll consider a scenario originally attributed to Wigner, and we'll work in an extension of the setting introduced in [BB19^[3]]. For brevity, we'll omit detailed computations in this section and focus on the higher level ideas instead. Consider a joint system consisting of three parts, a spin- $\frac{1}{2}$ particle $S$ , a friend $F$ in a lab, making observations of $S$ , and Wigner $W$ making observations of the lab (the joint friend-particle system $F S$ ). Figure of the joint system containing Wigner, the friend and a qubit Let the observation and action sets of the agents $F$ and $W$ be $O_{F} = {o_{0}^{F}, o_{1}^{F}},$ $A_{F} = {a_{0}^{F}, a_{1}^{F}},$ $O_{W} = {L_{00}^{+}, L_{00}^{-}, L_{11}^{+}, L_{11}^{-}},$ $A_{W} = {a_{0}^{W}, a_{1}^{W}},$ respectively. Assume the state spaces for $F$ and $W$ are given by their individual memory tape states $H_{F}$ and $H_{W}$ as described in Section 2. Suppose the spin- $\frac{1}{2}$ particle is initially in the state $∣ ∣ ψ_{0}^{S} ⟩ = | + ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩) \in H_{S} .$ The friend then measures $S$ in the ${| 0 ⟩, | 1 ⟩}$ basis, and performs an action $a_{F} \in A_{F}$ according to the policy $π^{F} \in Γ_{F} = A_{F}^{O_{F}} .$ The lab $L = F S$ then evolves unitarily to the state $| ψ_{L} ⟩ = \frac{1}{\sqrt{2}} ({∣ ∣ o_{0}^{F} π^{F} (o_{0}^{F}) ⟩}_{F} {| 0 ⟩}_{S} + {∣ ∣ o_{1}^{F} π^{F} (o_{1}^{F}) ⟩}_{F} {| 1 ⟩}_{S}),$ where $o_{0}^{F}, o_{1}^{F} \in O_{F}$ correspond to $F$ observing $0$ or $1$ respectively. Finally, suppose Wigner measures the lab $L = F S$ in the following basis: $\begin{matrix} ∣ ∣ L_{00}^{+} ⟩ & = \frac{1}{\sqrt{2}} ({∣ ∣ o_{0}^{F} a_{0}^{F} ⟩}_{F} {| 0 ⟩}_{S} + {∣ ∣ o_{1}^{F} a_{0}^{F} ⟩}_{F} {| 1 ⟩}_{S}), ∣ ∣ L_{00}^{-} ⟩ & = \frac{1}{\sqrt{2}} ({∣ ∣ o_{0}^{F} a_{0}^{F} ⟩}_{F} {| 0 ⟩}_{S} - {∣ ∣ o_{1}^{F} a_{0}^{F} ⟩}_{F} {| 1 ⟩}_{S}), ∣ ∣ L_{11}^{+} ⟩ & = \frac{1}{\sqrt{2}} ({∣ ∣ o_{0}^{F} a_{1}^{F} ⟩}_{F} {| 0 ⟩}_{S} + {∣ ∣ o_{1}^{F} a_{1}^{F} ⟩}_{F} {| 1 ⟩}_{S}), ∣ ∣ L_{11}^{-} ⟩ & = \frac{1}{\sqrt{2}} ({∣ ∣ o_{0}^{F} a_{1}^{F} ⟩}_{F} {| 0 ⟩}_{S} - {∣ ∣ o_{1}^{F} a_{1}^{F} ⟩}_{F} {| 1 ⟩}_{S}) . \end{matrix}$ So the two $L_{00}$ vectors correspond to states of the lab where the action of $F$ was $a_{0}^{F}$ (regardless of observation), and $L_{11}$ vectors correspond to states where the action was $a_{1}$ . Technically these four vectors are not a basis of the full $H_{L} = H_{F} \otimes H_{S}$ , since $dim (H_{L}) = 8$ . Nevertheless, $| ψ_{L} ⟩$ always falls within the four dimensional subspace spanned by these. If we wanted to be more precise, we could add further observation(s) to $O_{W}$ , corresponding to the complement of this four dimensional subspace, but this wouldn't affect our discussion here, and would introduce additional notation.

Now let's assume $F$ follows the constant policy $π_{00}^{F} (o_{i}^{F}) = a_{0}^{F}$ (for $i = 0, 1$ ). Then Wigner will observe $L_{00}^{+}$ with probability $1$ . Yet, if the friend $F$ believes that having observed $o_{i}^{F}$ , the state of the lab collapsed to ${∣ ∣ o_{i}^{F} a_{0}^{F} ⟩}_{F} {| i ⟩}_{S}$ , then the friend would expect Wigner to observe $L_{00}^{+}$ or $L_{00}^{-}$ with probability $\frac{1}{2}$ each. Thus, within collapse theories we have an apparent conflict between the predictions of Wigner and the friend.

We can model this scenario within IBP by taking $Γ = Γ_{F} \times Γ_{W} = A_{F}^{O_{F}} \times A_{W}^{O_{W}}$ be the pairs of policies of Wigner and the friend. Analogously to Definition 4.6 we can define $Φ_{U}$ as the joint outcome of all observables on the joint triple system $W F S$ , a kernel $β_{U} : Γ \to □ Φ_{U}$ , and the corresponding belief $Θ_{U} = ⊤_{Γ} ⋉ β_{U} \in □ (Γ \times Φ_{U}),$ and its projected bridge transform $Θ_{U}^{*} \in □ {el}^{Γ}$ . To be more precise we would again build this out of finite subsets of $U$ , as in Definition 4.7.

Given this setup, we can write down various definitions. For $h^{W} \in O_{W}$ , let $α_{h^{W} | π^{W}} = {(γ^{F}, γ^{W}) \in Γ | γ^{W} (h^{W}) = π^{W} (h^{W})} \in 2^{Γ},$ $q_{h^{W} | π^{W}} = {α \in 2^{Γ} | α \subset α_{h^{W} | π^{W}}} \subset 2^{Γ} .$ Then we can compute $E_{Θ_{U}^{*}} [χ_{π_{00}^{F}, π^{W}} (1 - χ_{q_{L_{00}^{+} | π^{W}}})] = 0,$ i.e. the observation $L_{00}^{+}$ of Wigner is certain to be instantiated if $F$ follows the policy $π_{00}^{F}$ .

We can also write down other quantities, for example for $h^{F} \in O_{F}$ , $h^{W} \in O_{W}$ , we can define $α_{h^{F}, h^{W} | π^{F}, π^{W}} = {(γ^{F}, γ^{W}) \in Γ | γ^{W} (h^{W}) = π^{W} (h^{W}), γ^{F} (h^{F}) = π^{F} (h^{F})} \in 2^{Γ},$ and the analogous $q_{h^{F}, h^{W} | π^{F}, π^{W}}$ . The quantity $E_{Θ_{U}^{*}} [χ_{π_{00}^{F}, π^{W}} (1 - χ_{q_{o_{0}, L_{00}^{+} | π_{00}^{F}, π^{W}}})]$ would then be the ultraprobability of the pair ( $W$ observing $L_{00}^{+}$ , $F$ observing $o_{0}$ ) being uninstantiated. We can estimate the value of this ultraprobability using techniques similar to Section 6 to be around $0.35$ .

This setting is helpful to differentiate the decision theory of IBP from a collapse theory. For example, consider a loss function $ℓ : O_{W} \to R_{\geq 0}$ that depends only on Wigner's observation, with values: $\begin{matrix} ℓ (L_{00}^{+}) & = 0, ℓ (L_{00}^{-}) & = 1, ℓ (L_{11}^{+}) & = 0.1, ℓ (L_{11}^{-}) & = 0.1. \end{matrix}$ Now suppose the friend is trying to minimize $ℓ$ .^[4] Then assuming a unitary evolution of the lab, clearly $π_{00}^{F}$ is the optimal policy. However, if the friend assumes a collapse of the lab after her observation, then always choosing action $a_{1}^{F} \in A_{F}$ avoids ever having an overlap with the high-loss $L_{00}^{-}$ , making the constant $a_{1}^{F}$ policy $π_{11}^{F} \in Γ_{F}$ optimal under the collapse interpretation.

We can consider this decision problem within IBP by working with the physicalized loss function $ℓ^{phys} : {el}^{Γ} \to R_{\geq 0}$ (cf. Definition 4.21), given by ^[5] $ℓ^{phys} (γ, α) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} 0 if \forall ~ γ \in α : {~ γ}^{W} (L_{00}^{+}) = γ^{W} (L_{00}^{+}) 0.1 else if \forall ~ γ \in α : {~ γ}^{W} (L_{11}^{+}) = γ^{W} (L_{11}^{+}) 0.1 else if \forall ~ γ \in α : {~ γ}^{W} (L_{11}^{-}) = γ^{W} (L_{11}^{-}) 1 otherwise. \end{matrix}$ Then in IBP the friend would look for the policy minimizing the loss $ℓ^{IBP} (π^{F}) = E_{Θ_{U}^{*}} [χ_{π^{F}} \cdot ℓ^{phys}] .$ We can verify that the minimal loss $ℓ^{IBP} (π^{F}) = 0$ occurs exactly when $π^{F} = π_{00}^{F}$ as expected, in contrast with the collapse interpretation.

6. Bounds on the ultraprobabilities

We'll make use of the following observation.

Lemma 6.1. For a given history $h \in O^{t}$ , if two policies $π_{1}, π_{2} \in Γ$ agree on all prefixes of $h$ , i.e. $π_{1} (~ h) = π_{2} (~ h) for all ~ h ⊏ h,$ then $Q_{h} U_{π_{1}}^{t} | ψ_{0} ⟩ = Q_{h} U_{π_{2}}^{t} | ψ_{0} ⟩,$ where $Q_{h}$ is the projection corresponding to the observation $obs (τ) = h$ , i.e. the memory tape having recorded $h$ .

Proof. For $t = 1$ we have $U_{π_{1}} | ψ_{0} ⟩ = \sum o \in O | o π_{1} (o) ⟩ \otimes U_{π_{1} (o)} P_{o} ∣ ∣ ψ_{0}^{e} ⟩,$ and similarly for $π_{2}$ . Now for $h = o_{i}$ we have $Q_{h} U_{π_{1}} | ψ_{0} ⟩ = | o_{i} π_{1} (o_{i}) ⟩ \otimes U_{π_{1} (o_{i})} P_{o_{i}} ∣ ∣ ψ_{0}^{e} ⟩ = Q_{h} U_{π_{2}} | ψ_{0} ⟩,$ since $π_{1} (h) = π_{2} (h)$ by assumption. For $t > 1$ we can proceed by induction, using Lemma 4.11. $\begin{matrix} □ \end{matrix}$

6.1. Upper bound

To prove an upper bound on the expectation value, we can coarsen our set of physical states to only include measurements of the memory tape.

Let $D = E^{T} \subset {Tp}_{T}$ be the set of destinies.

Definition 6.2. Let $B_{D}$ be the universal observable corresponding to reading the destiny off the memory tape at time $t_{B_{D}} = T$ . That is, $V_{B_{D}} = D$ , and for $d \in D$ $Q_{B_{D}} (d) : H^{g} \to H^{g}$ is given by $∣ ∣ ψ_{τ}^{g} ⟩ \otimes | ψ^{e} ⟩ \mapsto {\begin{matrix} ∣ ∣ ψ_{τ}^{g} ⟩ \otimes | ψ^{e} ⟩ & if τ = d 0 & otherwise . \end{matrix}$

Definition 6.3. Let $Q \subset Γ \times D$ be the relation of a destiny being compatible with a policy. That is, $(π, d) \in Q$ for $d = (o_{1}, a_{1}, \dots, o_{T}, a_{T})$ if and only if $a_{i} = π (o_{1}, \dots, o_{i})$ for each $1 \leq i \leq T$ .

Let $F_{D} = {B_{D}}$ , and note that $Φ_{F_{D}} = V_{B_{D}} = D$ . Let $β_{F_{D}} : Γ \to Δ D$ be the corresponding kernel.

Lemma 6.4. The kernel $β_{F_{D}} : Γ \to Δ D$ is a PoCK for $Q$ .

Proof. This is essentially saying that whenever $π_{1}, π_{2} \in Γ$ are both compatible with a destiny $d \in D$ , then $β_{F_{D}} (d | π_{1}) = β_{F_{D}} (d | π_{2}) .$ This claim follows by Lemma 6.1. $\begin{matrix} □ \end{matrix}$

Then by [IBP Proposition 4.1] we have

Lemma 6.5. The bridge transform equals $Br (Θ_{F_{D}}) = [⊤_{Γ} ⋉ (Q^{- 1} ⋊ β_{F_{D}})]^{↓} .$ In particular, for a monotone increasing (in $2^{Γ}$ ) function $f : Γ \times 2^{Γ} \to [0, 1]$ , we have $\begin{matrix} \begin{matrix} E_{Θ_{F_{D}}^{*}} [f] = max γ \in Γ E_{β_{F_{D}} (γ)} [f (γ, -) \circ Q^{- 1}] . \end{matrix} \\ (1) \end{matrix}$

For $g = χ_{q_{E | π}}$ (note that $g$ is monotone decreasing) and $d \in D$ we have $g (γ, -) \circ Q^{- 1} (d) = 1$ if

$γ = π$ ,
$π \in Q^{- 1} (d)$ , and
$Q^{- 1} (d) \subset α_{h | π}$ for some $h \in E$ .

Lemma 6.6. We have $Q^{- 1} (d) \subset α_{h | π}$ if and only if $h = obs (d)$ and $a_{T} = π (h)$ (where $d = (o_{1}, a_{1}, \dots, o_{T}, a_{T})$ as before).

Proof. If $h = obs (d)$ and $a_{T} = π (h)$ , then $(γ, d) \in Q$ implies $γ (h) = a_{T} = π (h)$ , so $Q^{- 1} (d) \subset α_{h | π}$ .

For the converse, assume $Q^{- 1} (d) \subset α_{h | π}$ . First choose $γ \in Q^{- 1} (d)$ (which is always non-empty). In particular $γ (h) = a_{T}$ , so $γ \in α_{h | π}$ means $π (h) = a_{T}$ as well.

Now assume $h \neq obs (d)$ . Then choose $γ^{'} \in Γ$ as follows. For $~ h \in O^{\leq T}$ , let $γ^{'} (~ h) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} a_{i} & if ~ h = (o_{1}, \dots, o_{i}) {~ a}_{T} \neq a_{T} & if ~ h = h a_{1} (arbitrary) & otherwise. \end{matrix}$ Then $γ^{'} \in Q^{- 1} (d) ∖ α_{h | π}$ , contradiction. $\begin{matrix} □ \end{matrix}$

We therefore have $E_{β_{F_{D}} (γ)} [χ_{q_{E | π}} (γ, -) \circ Q^{- 1}] = ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} \sum h \in E \sum \begin{matrix} d \in Q (π) h = obs (d) \end{matrix} β_{F_{D}} (π) (d) & if γ = π 0 & otherwise . \end{matrix}$ Here $\sum h \in E \sum \begin{matrix} d \in Q (π) h = obs (d) \end{matrix} β_{F_{D}} (π) (d) = Cop (E | π),$ so by applying $(1)$ of Lemma 6.5 to the monotone increasing $f = χ_{π} (1 - χ_{q_{E | π}})$ , we have $E_{Θ_{F_{D}}^{*}} [χ_{π} (1 - χ_{q_{E | π}})] = 1 - Cop (E | π),$ since $χ_{π} (γ, α) = 0$ whenever $γ \neq π$ so the ${max}_{γ \in Γ}$ is attained when $γ = π$ . Since $Θ_{U}^{*} \subset Θ_{F_{D}}^{*}$ by definition, we have Proposition 6.7. $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{E | π}})] \leq 1 - Cop (E | π) .$

6.2. Lower bound

Definition 6.8. For ease of notation we'll write $C_{E | π} := 1 - \sqrt{(2 - Cop (E | π)) Cop (E | π)} .$

Theorem 6.9. We have a lower bound $E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{E | π}})] \geq C_{E | π} .$

Proof. We'll exhibit a contribution $ρ_{E | π} \in Δ^{c} {el}^{Γ}$ (Definition 6.12) such that $ρ_{E | π} \in Θ_{U}^{*}$ (Proposition 6.18). The constructed $ρ_{E | π}$ has (Lemma 6.13) $E_{ρ_{E | π}} [χ_{π} (1 - χ_{q_{E | π}})] = C_{E | π},$ which in turn will show that $\begin{matrix} E_{Θ_{U}^{*}} [χ_{π} (1 - χ_{q_{E | π}})] = max ρ \in Θ_{U}^{*} E_{ρ} [χ_{π} (1 - χ_{q_{E | π}})] \geq E_{ρ_{E | π}} [χ_{π} (1 - χ_{q_{E | π}})] = C_{E | π} . \end{matrix}$ $\begin{matrix} □ \end{matrix}$

The rest of this section is dedicated to spelling out the results that are used in the proof outline above.

Lemma 6.10. Let $| a ⟩, | b ⟩, | c ⟩$ be a set of three orthonormal vectors, and $| ϕ ⟩ = α | a ⟩ + β | b ⟩,$ $| ψ ⟩ = α | a ⟩ + β | c ⟩,$ where $α, β \in C$ with $| α |^{2} + | β |^{2} = 1$ . Then the trace distance between the density matrices $ρ = | ϕ ⟩ ⟨ ϕ |$ and $σ = | ψ ⟩ ⟨ ψ |$ is $d_{t r} (ρ, σ) = \frac{1}{2} ∥ ρ - σ ∥_{1} = \sqrt{1 - | α |^{4}} .$

Proof. In the basis given by $| a ⟩, | b ⟩, | c ⟩$ , the matrix of $ρ - σ$ is $⎛ ⎜ ⎜ ⎝ \begin{matrix} | α |^{2} & α ¯ β & 0 ¯ α β & | β |^{2} & 0 0 & 0 & 0 \end{matrix} ⎞ ⎟ ⎟ ⎠ - ⎛ ⎜ ⎜ ⎝ \begin{matrix} | α |^{2} & 0 & α ¯ β 0 & 0 & 0 ¯ α β & 0 & | β |^{2} \end{matrix} ⎞ ⎟ ⎟ ⎠ = ⎛ ⎜ ⎜ ⎝ \begin{matrix} 0 & α ¯ β & - α ¯ β ¯ α β & | β |^{2} & 0 - ¯ α β & 0 & - | β |^{2} . \end{matrix} ⎞ ⎟ ⎟ ⎠$ The eigenvalues of this (rank 2) matrix are $0$ , and $\pm \sqrt{1 - | α |^{4}}$ , so the sum of the absolute values of the eigenvalues is $∥ ρ - σ ∥_{1} = 0 + \sqrt{1 - | α |^{4}} + \sqrt{1 - | α |^{4}} = 2 \sqrt{1 - | α |^{4}} .$ $\begin{matrix} □ \end{matrix}$

Lemma 6.11. For two policies $π_{1}, π_{2}$ , let $Π_{12} = {d \in O^{T} : \forall h ⊏ d, π_{1} (h) = π_{2} (h)},$ $E_{12} = O^{T} ∖ Π_{12} .$ Then for any $B \in U$ , $E_{β_{B} (π_{1}) \land β_{B} (π_{2})} [1] \geq C_{E_{12} | π_{1}} .$

Proof. Roughly speaking, since $π_{1}$ and $π_{2}$ only differ outside of $Π_{12}$ , if the event $Π_{12}$ was observed then $π_{1}$ and $π_{2}$ behave identically. More precisely, let $h_{B} \in O^{t_{B}}$ be a sequence of observations up to time $t_{B}$ . Then, if $h_{B} ⊏ d$ for some $d \in Π_{12}$ , by Lemma 6.1 we have $\begin{matrix} \begin{matrix} Q_{h_{B}} U_{π_{1}}^{t_{B}} | ψ_{0} ⟩ = Q_{h_{B}} U_{π_{2}}^{t_{B}} | ψ_{0} ⟩ . \end{matrix} \\ (1) \end{matrix}$ Without loss of generality we'll assume $t_{B} = T$ from now on. Now, $U_{π_{1}}^{T} | ψ_{0} ⟩ = \sum h \in O^{T} Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩ = \sum h \in Π_{12} Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩ + \sum h \in O^{T} ∖ Π_{12} Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩,$ and similarly for $π_{2}$ . Write $| π_{1} \cap π_{2} ⟩ := \sum h \in Π_{12} Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩ = \sum h \in Π_{12} Q_{h} U_{π_{2}}^{T} | ψ_{0} ⟩,$ where the two sums are equal by $(1)$ . Also write $| π_{1} ∖ π_{2} ⟩ := \sum h \in O^{T} ∖ Π_{12} Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩,$ and $| π_{2} ∖ π_{1} ⟩ := \sum h \in O^{T} ∖ Π_{12} Q_{h} U_{π_{2}}^{T} | ψ_{0} ⟩,$ so that $U_{π_{1}}^{T} | ψ_{0} ⟩ = | π_{1} \cap π_{2} ⟩ + | π_{1} ∖ π_{2} ⟩,$ and $U_{π_{2}}^{T} | ψ_{0} ⟩ = | π_{1} \cap π_{2} ⟩ + | π_{2} ∖ π_{1} ⟩ .$ The three vectors $| π_{1} \cap π_{2} ⟩$ , $| π_{1} ∖ π_{2} ⟩$ , $| π_{2} ∖ π_{1} ⟩$ are orthogonal (since all of their $H^{g}$ components are), and $∥ | π_{1} \cap π_{2} ⟩ ∥^{2} = \sum h \in Π_{12} ∥ Q_{h} U_{π_{1}}^{T} | ψ_{0} ⟩ ∥^{2} = \sum h \in Π_{12} Cop (h | π_{1}) = Cop (Π_{12} | π_{1}) .$ From this, using Lemma 6.10, we can compute the trace distance between $ρ_{π_{1}} = ∣ ∣ U_{π_{1}}^{T} ψ_{0} ⟩ ⟨ U_{π_{1}}^{T} ψ_{0} ∣ ∣$ and $ρ_{π_{2}} = ∣ ∣ U_{π_{2}}^{T} ψ_{0} ⟩ ⟨ U_{π_{2}}^{T} ψ_{0} ∣ ∣$ to be $d_{t r} (ρ_{π_{1}}, ρ_{π_{2}}) = \frac{1}{2} ∥ ρ_{π_{1}} - ρ_{π_{2}} ∥_{1} = \sqrt{1 - ∥ | π_{1} \cap π_{2} ⟩ ∥^{4}} = \sqrt{1 - Cop (Π_{12} | π_{1})^{2}} .$

Now, for any measurement $Q_{B}$ , if we write $β_{B} (v | π_{1}) = ∥ Q_{B} (v) U_{π_{1}}^{T} | ψ_{0} ⟩ ∥^{2}$ for the distribution of outcomes, where $v \in V_{B}$ . Then the total variation distance between the distributions $β_{B} (- | π_{1})$ and $β_{B} (- | π_{2})$ is bounded above by the trace distance. That is, $d_{T V} (β_{B} (- | π_{1}), β_{B} (- | π_{2})) = \frac{1}{2} \sum v \in V_{B} | β_{B} (v | π_{1}) - β_{B} (v | π_{2}) | \leq d_{t r} (ρ_{π_{1}}, ρ_{π_{2}}) .$ So the overlap is bounded below as claimed $\begin{matrix} E_{β_{B} (π_{1}) \land β_{B} (π_{2})} [1] = 1 - d_{T V} (β_{B} (- | π_{1}), β_{B} (- | π_{2})) \geq 1 - d_{t r} (ρ_{π_{1}}, ρ_{π_{2}}) = 1 - \sqrt{1 - Cop (Π_{12} | π_{1})^{2}} = C_{E_{12} | π_{1}} . \end{matrix}$ $\begin{matrix} □ \end{matrix}$

Definition 6.12. Given a policy $π$ and an event $E \subset O^{T}$ , choose ${~ π}_{E} \in Γ$ such that $\begin{matrix} {~ π}_{E} (h) \neq π (h) whenever \forall d \in D : h ⊏ d ⟹ d \in E {~ π}_{E} (h) = π (h) otherwise. \end{matrix}$ Note that we are using $| A | > 1$ here to allow the choice satisfying the first condition. That is, ${~ π}_{E}$ agrees with $π$ on all histories except for the ones whose completions all lie in $E$ . Let $ρ_{E | π} = C_{E | π} \cdot δ_{π, {π, {~ π}_{E}}} \in Δ^{c} {el}^{Γ} .$

Lemma 6.13. We have $E_{ρ_{E | π}} [χ_{π} (1 - χ_{q_{E | π}})] = C_{E | π} .$

Proof. The claim follows since ${π, {~ π}_{E}} \subset̸ α_{h | π}$ for any $h \in E$ . $\begin{matrix} □ \end{matrix}$

Definition 6.14. Let $ϕ_{B} = \frac{C_{E | π}}{E_{β_{B} (π) \land β_{B} ({~ π}_{E})} [1]} β_{B} (π) \land β_{B} ({~ π}_{E}) .$

Lemma 6.15. The contribution $ϕ_{B}$ has mass $C_{E | π}$ , i.e. $E_{ϕ_{B}} [1] = C_{E | π}$ . Moreover, $ϕ_{B} \leq β_{B} (π) \land β_{B} ({~ π}_{E}) .$

Proof. The mass follows from the definition. The inequality in the second claim follows by taking $π_{1} = π$ and $π_{2} = {~ π}_{E}$ in Lemma 6.11, and noticing that the $E_{12}$ in the lemma equals $E$ in this case. $\begin{matrix} □ \end{matrix}$

Lemma 6.16. For finite $F \subset U$ , let $ϕ_{F} = \frac{1}{C_{E | π}^{| F | - 1}} \prod B \in F ϕ_{B} \in Δ^{c} Φ_{F} .$ Then $ϕ_{F} \in β_{F} (π) \cap β_{F} ({~ π}_{E}) \subset Δ^{c} Φ_{F}$ .

Proof. For any $f \in F$ , consider the projection ${pr}_{f} : Φ_{F} = \prod B \in F V_{B} \to V_{f} .$ Then under $({pr}_{f})_{*} : Δ^{c} Φ_{F} \to Δ^{c} V_{f}$ we have $({pr}_{f})_{*} (ϕ_{F}) = \frac{1}{C_{E | π}^{| F | - 1}} ϕ_{f} \prod B \in F ∖ {f} E_{ϕ_{B}} [1] = \frac{C_{E | π}^{| F | - 1}}{C_{E | π}^{| F | - 1}} ϕ_{f} = ϕ_{f} \leq β_{f} (π) \land β_{f} ({~ π}_{E}),$ where the last inequality follows from Lemma 6.15. Since this is true for all $f$ , we have $ϕ_{F} \in ⋈ B \in F β_{B} (π) = β_{F} (π) \in □ Φ_{F},$ and also $ϕ_{F} \in β_{F} ({~ π}_{E})$ , hence $ϕ_{F} \in β_{F} (π) \cap β_{F} ({~ π}_{E})$ . $\begin{matrix} □ \end{matrix}$

Proposition 6.17. For each finite $F \subset U$ , we have $δ_{π, {π, {~ π}_{E}}} \times ϕ_{F} \in Br (Θ_{F}) \subset Δ^{c} ({el}^{Γ} \times Φ_{F}),$ and hence $ρ_{E | π} = C_{E | π} \cdot δ_{π, {π, {~ π}_{E}}} \in {pr}_{*} (Br (Θ_{F})) = Θ_{F}^{*} .$

Proof. Let $s : Γ \to Γ$ be an endomorphism of the computational universe. We need to verify that for any such $s$ , under the composite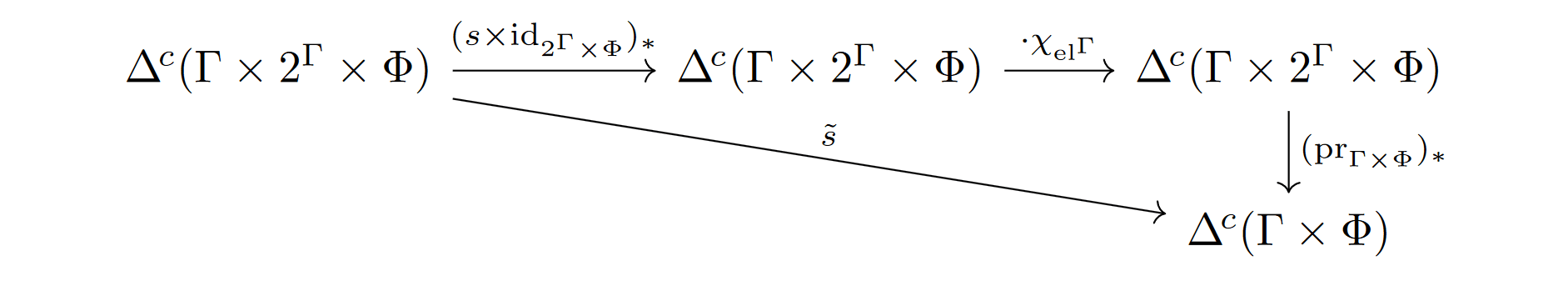 Commutative diagram defining the bridge transform we have $~ s (δ_{π, {π, {~ π}_{E}}} \times ϕ_{F}) \in Θ_{F}$ . Since $ρ_{E | π} = C_{E | π} \cdot δ_{π, {π, {~ π}_{E}}}$ , we have $χ_{{el}^{Γ}} \neq 0$ only when $s (π) = π$ or $s (π) = {~ π}_{E}$ . For these cases, we have

If $s (π) = π$ , then $~ s (δ_{π, {π, {~ π}_{E}}} \times ϕ_{F}) = δ_{π} \times ϕ_{F} \in Θ_{F},$ since $ϕ_{F} \in β_{F} (π)$ by Lemma 6.16.
If $s (π) = {~ π}_{E}$ , then $~ s (δ_{π, {π, {~ π}_{E}}} \times ϕ_{F}) = δ_{{~ π}_{E}} \times ϕ_{F} \in Θ_{F},$ since $ϕ_{F} \in β_{F} ({~ π}_{E})$ as well by Lemma 6.16. $\begin{matrix} □ \end{matrix}$

Proposition 6.18. We have $ρ_{E | π} = C_{E | π} \cdot δ_{π, {π, {~ π}_{E}}} \in Θ_{U}^{*} .$

Proof. This follows immediately from Proposition 6.17 and the Definition 4.7 of $Θ_{U}^{*}$ . $\begin{matrix} □ \end{matrix}$

7. Asymptotic convergence

7.1. Upper bound

Theorem 7.1. For any policy $π$ , $L^{IBP} (π) \leq L^{Cop} (π),$ where the two sides are as in Definition 4.22.

Proof. Using the notation from Section 6, we can apply $(1)$ of Lemma 6.5 to the monotone increasing $f = χ_{π} \cdot L^{phys}$ , to get $E_{Θ_{F_{D}}^{*}} [χ_{π} \cdot L^{phys}] = E_{β_{F_{D}} (π)} [L^{phys} \circ Q^{- 1}],$ since the maximum over $γ \in Γ$ is attained when $γ = π$ , due to the $χ_{π}$ factor. We have that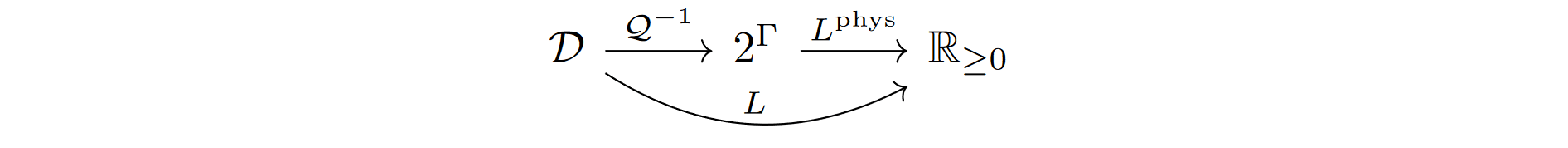 Diagram of recovering subjective loss from its physicalized version commutes, i.e. $L = L^{phys} \circ Q^{- 1}$ . To see this, note that $h \in X_{Q^{- 1} (d)}$ if and only if $h ⊏ d$ , by an argument analogous to Lemma 6.6, hence $L^{phys} (Q^{- 1} (d)) = min h ⊏ d max ~ d ⊐ h L (d) = L (d) .$ Therefore, $E_{β_{F_{D}} (π)} [L^{phys} \circ Q^{- 1}] = E_{β_{F_{D}} (π)} [L] = L^{Cop} (π),$ and so by refinement $L^{IBP} (π) = E_{Θ_{U}^{*}} [χ_{π} \cdot L^{phys}] \leq E_{Θ_{F_{D}}^{*}} [χ_{π} \cdot L^{phys}] = L^{Cop} (π) .$ $\begin{matrix} □ \end{matrix}$

7.2. Asymptotic behavior of communicating MDPs

This section introduces some general definitions and lemmas in the theory of Markov decision processes. Our main goal here is to state and prove Proposition 7.17, concerning the asymptotic behavior of a communicating MDP. None of these results are to be considered original, but are intended as an overview for the reader, as well as a way to establish the exact form of an asymptotic bound that we need (which we couldn't find verbatim in the literature).

Definition 7.2. Let a finite Markov decision process (MDP) be given by the following data (cf. [Put94^[6] Section 2.1]).

A finite set of states $S$ ,
a finite set of actions $A$ ,
a transition kernel $κ : S \times A \to Δ S$ ,
and a loss function $ℓ : S \times A \to R$ .

Remark 7.3. The above setting is not the most general one (for example, we could let the set of actions $A_{s}$ depend on the state, or allow the loss function $ℓ : S \times A \to Δ R$ to be stochastic). The simplifying assumptions we make in the above definition are mostly for the ease of discussion rather than strictly necessary. Some of the results might need additional assumptions in the more general setting, e.g. for Proposition 7.17 we might want to assume that a stochastic $ℓ$ is still bounded.

Definition 7.4. For $t \in N$ , let $H_{t} = (S \times A)^{t} \times S$ be the set of histories up to time $t$ , $H = ⨆ t < T H_{t}$ be histories up to some time horizon $T$ , and $Γ = (Δ A)^{H}$ be the set of (randomized, history-dependent, cf. [Put94^[6:1] Section 2.1.4]) policies.

Remark 7.5. We allow randomized policies here, simply because our discussion in this subsection fits naturally with that generality, and also since it seems common to do so in the classical MDP literature. Note however that optimal policies for an MDP can always be chosen to be deterministic, so our discussion is still compatible with the quantum case, where we only allowed deterministic policies (cf. Remark 2.3).

Definition 7.6 (Time evolution of an MDP). For a given policy $π : H \to Δ A$ , and an initial state $h_{0} \in Δ S$ , we can define recursively for each $t \in N$ a distribution $σ_{t}^{π} \in Δ H_{t}$ as follows. Take $σ_{0}^{π} = h_{0}$ , and consider $H_{t} π_{t} - \to Δ A .$ We can then form $α_{t}^{π} = σ_{t}^{π} ⋉ π_{t} \in Δ (S \times A)^{t + 1}$ . Now we can compose $(S \times A)^{t + 1} {pr}_{t + 1} - -- \to S \times A κ \to Δ S,$ where ${pr}_{i}$ is projection onto the $i$ ^th factor. Then we can let $σ_{t + 1}^{π} = α_{t}^{π} ⋉ [κ \circ {pr}_{t + 1}] \in Δ H_{t + 1} .$ We let $σ^{π} | σ_{0} := σ_{T}^{π}$ be the resulting distribution on destinies $D = H_{T}$ , $σ^{π} | σ_{0} \in Δ D .$ More generally, we can begin with a condition at time $k$ , given by $h_{k} \in Δ H_{k}$ , and follow the time evolution above to a distribution $σ^{π} | h_{k} \in Δ D .$ For a subset $U \subset D$ , we'll write $P_{π} [U | h_{k}]$ for the probability of $U$ , and for a function $f : D \to R$ , we'll write $E_{π} [f | h_{k}]$ for the expected value of $f$ with respect to $σ^{π} | h_{k}$ .

Definition 7.7. For $t = 1, \dots, T$ , define $ℓ_{t} : D \to R$ by $ℓ_{t} (d) = ℓ ({pr}_{t} (d)) .$ and let $L_{t} : D \to R$ be the total loss $L_{t} = T \sum τ = t ℓ_{τ} .$

Definition 7.8. We call an MDP communicating (cf [Put94^[6:2] Section 8.3]), if for any pair of states $s_{1}, s_{2} \in S$ , there exists a policy $π \in Γ$ and a time $n \in N$ such that $P_{π} [{pr}_{n}^{S} (d) = s_{2} | δ_{s_{1}}] > 0,$ where ${pr}_{n}^{S}$ extracts the $n$ ^th state of a destiny. Roughly speaking, a communicating MDP allows navigating between any two states with non-zero probability.

We now have all the definitions involved Proposition 7.17, our main result in this section. In the following, we'll introduce various definitions and lemmas that we'll make use of in the proof.

Definition 7.9. For a destiny $d \in D$ and a state $s \in S$ , define $θ_{s} : D \to Z_{+}$ by $θ_{s} (d) = min ({θ \in Z_{+} : {pr}_{θ}^{S} (d) = s} \cup {T + 1}),$ that is the first time at which state $s$ occurs (or $T + 1$ if $s$ doesn't occur). Let $Arr : S \times S \to R$ be given by $Arr (s_{1}, s_{2}) = min π \in Γ E_{π} [θ_{s_{2}} | δ_{s_{1}}],$ that is the minimum expected arrival time to $s_{2}$ , starting from $s_{1}$ .

Lemma 7.10. For a communicating MDP, there is a constant $N$ such that for any time horizon $T$ , $Arr (s_{1}, s_{2}) \leq N,$ for all $s_{1}, s_{2} \in S$ .

Proof. Let $s_{1}, s_{2} \in S$ be two states where the maximum ${max}_{s_{i} \in S} Arr (s_{1}, s_{2})$ is attained. Since the MDP is communicating, there exists a policy $π \in Γ$ and a time $n \in N$ such that $P_{π} [{pr}_{n}^{S} (d) = s_{2} | δ_{s_{1}}] = p > 0.$ Following this $π$ for $n$ timesteps (assuming $n < T$ , otherwise $Arr (s_{1}, s_{2}) \leq n / p$ trivially), we get $\begin{matrix} \begin{matrix} Arr (s_{1}, s_{2}) \leq \sum ~ s \in S P_{π} [{pr}_{n}^{S} (d) = ~ s | δ_{s_{1}}] (Arr (~ s, s_{2}) + n), \end{matrix} \\ (1) \end{matrix}$ by conditioning the state we land on on the $n$ ^th step. Now, $\begin{matrix} \sum ~ s \in S P_{π} [{pr}_{n}^{S} (d) = ~ s | δ_{s_{1}}] (Arr (~ s, s_{2}) + n) \leq ⎛ ⎝ \sum ~ s \in S ∖ {s_{2}} P_{π} [{pr}_{n}^{S} (d) = ~ s | δ_{s_{1}}] (Arr (~ s, s_{2}) + n) ⎞ ⎠ + p n \leq (1 - p) (Arr (s_{1}, s_{2}) + n) + p n, \\ (2) (3) \end{matrix}$ where $(2)$ follows from the assumption on the policy $π$ arriving to $s_{2}$ with probability $p$ after $n$ steps, and $(3)$ follows from our assumption on $Arr (s_{1}, s_{2})$ being maximal (so $Arr (~ s, s_{2}) \leq Arr (s_{1}, s_{2})$ ). Combining with $(1)$ , we get $Arr (s_{1}, s_{2}) \leq (1 - p) (Arr (s_{1}, s_{2}) + n) + p n,$ so $Arr (s_{1}, s_{2}) \leq \frac{n}{p} .$ $\begin{matrix} □ \end{matrix}$

Definition 7.11. For $t \in Z_{+}$ , let the value function $V_{t} : D \to R$ be given by $V_{t} (d) = min π \in Γ E_{π} [L_{t} | δ_{{pr}_{< t} (d)}],$ i.e. the minimal expected remaining loss after time $t$ , assuming the state at time $t$ agrees with $d$ . Here ${pr}_{< t} : D \to H_{t - 1}$ truncates to an initial history.

Remark 7.12. As defined above, the value function depends on the entire history ${pr}_{< t} (d) \in (S \times A)^{t - 1} \times S = H_{t - 1}$ , up to time $t$ . It turns out (see [Put94^[6:3] Theorem 4.4.2.]) that in fact it's determined by the last state, $s_{t} = {pr}_{t}^{S} (d)$ , of this history. By slight abuse of notation, we'll write $V_{t} : S \to R$ for the resulting function as well.

Lemma 7.13. For a communicating MDP, there exists a constant $K$ , such that for any time horizon $T$ , $max s \in S V_{t} (s) - min s \in S V_{t} (s) \leq K .$

Proof. Let $s_{1} \in {a r g m a x}_{s \in S} V_{t} (s)$ , and $s_{2} \in {a r g m i n}_{s \in S} V_{t} (s)$ . By Lemma 7.10, $Arr (s_{1}, s_{2}) \leq N$ , and let $π_{12}$ be a policy that attains $Arr (s_{1}, s_{2}) = min π \in Γ E_{π} [θ_{s_{2}} | δ_{s_{1}}] .$ Let $π_{2}^{*}$ be a policy that attains $V_{t} (s_{2}) = min π \in Γ E_{π} [L_{t} | σ_{t} = δ_{s_{2}}] .$ Now construct a policy $~ π = ‘ ‘ π_{12} ⊔ π_{2}^{*} "$ as follows. In words, $~ π$ follows $π_{12}$ from $s_{1}$ until arriving at $s_{2}$ , and from then on follows $π_{2}^{*}$ . Formally, we can write for a history $h \in H$ , $~ π (h) = {\begin{matrix} π_{12} ({pr}_{\geq t} (h)) if {pr}_{i}^{S} (h) \neq s_{2} for any t \leq i π_{2}^{*} ({pr}_{\geq k} (h)) where k \in N is smallest such that {pr}_{t + k}^{S} (h) = s_{2} . \end{matrix}$ (Note that we use ${pr}_{\geq i}$ as a way of shifting the history in time, for example ${pr}_{\geq 3} (s_{1} a_{1} s_{2} a_{2} s_{3} a_{3} s_{4} a_{4} s_{5}) = s_{3} a_{3} s_{4} a_{4} s_{5}$ .) Now, we have $V_{t} (s_{1}) \leq E_{~ π} [L_{t} | σ_{t} = δ_{s_{1}}],$ and we can write $L_{t} (d) = k - 1 \sum τ = 0 ℓ_{t + τ} + L_{t + k},$ where $k \in N$ is smallest such that ${pr}_{t + k}^{S} (d) = s_{2}$ . Here $k - 1 \sum τ = 0 ℓ_{t + τ} \leq k \cdot max ℓ,$ $L_{t + k} \leq L_{t} - k \cdot min ℓ,$ so $\begin{matrix} E_{~ π} [L_{t} | σ_{t} = δ_{s_{1}}] \leq E_{~ π} [θ_{s_{2}} | δ_{s_{1}}] \cdot max ℓ + E_{~ π} [L_{t} | δ_{s_{2}}] - E_{~ π} [θ_{s_{2}} | δ_{s_{1}}] \cdot min ℓ = E_{π_{2}^{*}} [L_{t} | δ_{s_{2}}] + E_{π_{12}} [θ_{s_{2}} | δ_{s_{1}}] (max ℓ - min ℓ) = V_{t} (s_{2}) + Arr (s_{1}, s_{2}) (max ℓ - min ℓ) \leq V_{t} (s_{2}) + K, \end{matrix}$

for $K = N (max ℓ - min ℓ)$ , where $N$ is as in Lemma 7.10. To summarize in words, starting from $s_{1}$ we can make it to $s_{1}$ in at most $N$ expected timesteps, accumulating at most $N \cdot max ℓ$ loss in expectation. Then we can follow the optimal policy starting at time $t + k$ from $s_{2}$ , and accumulate $V_{t + k} (s_{2})$ loss, which is at most $k \cdot min ℓ$ different from $V_{t} (s_{2})$ . Putting these together, we get $V_{t} (s_{1}) - V_{t} (s_{2}) \leq K = N (max ℓ - min ℓ)$ . $\begin{matrix} □ \end{matrix}$

Lemma 7.14. For any policy $π$ , and any $d \in D$ , $V_{t} (d) \leq E_{π} [ℓ_{t} + V_{t + 1} | δ_{{pr}_{< t} (d)}] .$

Proof. By the optimality of $V_{t} (d)$ , we have $V_{t} (d) = min a \in A q_{t} (s_{t}, a),$ where $s_{t} = {pr}_{t}^{S} (d)$ is the $t$ ^th state, and $q_{t} (s_{t}, a) = ℓ (s_{t}, a) + \sum s_{t + 1} \in S P_{κ} [s_{t + 1} | s_{t}, a] V_{t + 1} (s_{t + 1}) .$ On the other hand, $E_{π} [ℓ_{t} + V_{t + 1} | δ_{{pr}_{< t} (d)}] = E_{a \sim π (d_{< t})} [q (s_{t}, a)],$ i.e. the expected value of $q_{t} (s_{t}, a)$ when the action $a$ is distributed according to the policy $π (d_{< t}) \in Δ A$ . The inequality now follows. $\begin{matrix} □ \end{matrix}$

Definition 7.15. Let $D_{t} = ℓ_{t} - V_{t} + V_{t + 1} : D \to R$ .

Lemma 7.16. We have for any policy $π$ and initial state $h_{k} \in Δ H_{k}$ with $k < t$ , $E_{π} [D_{t} | h_{k}] \geq 0,$ and $| D_{t} | \leq C,$ for $C = max ℓ - min ℓ + K$ , where $K$ is as in Lemma 7.13.

Proof. Since, by Lemma 7.14 we have $E_{π} [D_{t} | δ_{h}] \geq 0$ for any history $h \in H_{t - 1}$ , the same holds for any distribution of histories, in particular also for the $σ_{t - 1}^{π} \in Δ H_{t - 1}$ given by the time evolution of $h_{k}$ . We also have $min s \in S V_{t} (s) \leq V_{t} \leq max s \in S V_{t} (s),$ $min s \in S V_{t} (s) - max ℓ \leq V_{t + 1} \leq max s \in S V_{t} (s) - min ℓ,$ from which $| D_{t} | \leq C$ follows. $\begin{matrix} □ \end{matrix}$

Proposition 7.17. For a communicating MDP, there is a constant $C$ such that for any policy $π$ and initial state $h_{0}$ , $P_{π} [L_{1} \leq L^{*} - ϵ | h_{0}] < δ$ holds whenever $ϵ^{2} > 2 T C^{2} log \frac{1}{δ},$ where $L^{*} = min π \in Γ E_{π} [L_{1} | h_{0}]$ is the minimal expected loss. In words, it's unlikely (under any policy and initial state) for the total loss to be much below the minimal expected loss.

Proof. We have $L_{1} - V_{1} = T \sum t = 1 D_{t},$ where $Y_{t} = \sum_{τ = 1}^{t} D_{τ}$ is a bounded sub-martingale by Lemma 7.16, so by Azuma's inequality we get $P_{π} [(L_{1} - V_{1} \leq - ϵ) | h_{0}] \leq exp (\frac{- ϵ^{2}}{2 T C^{2}}) .$ Since this holds for all $h_{0}$ , and $L^{*} = E_{h_{0}} [V_{1}]$ , we also get the stated result. $\begin{matrix} □ \end{matrix}$

7.3. Lower bound

We can use the result above to obtain a lower bound on $L^{IBP}$ .

Definition 7.18. Assume we have the setup of a system given in Section 2, and furthermore that $O$ is a complete set of observations (so each $P_{o}$ has a 1-dimensional image). Then given a loss function $ℓ : O \times A \to R_{\geq 0}$ , there's a Markov decision process associated with this setting, where the set of states is $S = O$ , and the transition probabilities $κ : S \times A \to Δ S$ are given via the Born rule: $P_{κ} [o_{2} | o_{1}, a] = ∥ P_{o_{2}} U_{a} ∣ ∣ ψ_{o_{1}} ⟩ ∥^{2},$ where $∣ ∣ ψ_{o_{1}} ⟩$ is a unit vector in the image of $P_{o_{1}}$ .

Remark 7.19. It might be interesting to also consider the case where $O$ is incomplete. In this case there's an associated POMDP (partially obvervable Markov decision process). Note, however that a priori this POMDP will have infinitely many states (all rays in the image of $P_{o}$ for each $o \in O$ ). We won't pursue this direction here.

Remark 7.20. To understand the structure of the resulting MDP a little better, consider the following. For two observations $o_{1}, o_{2}$ , let's say that $o_{1} \geq o_{2}$ ( $o_{2}$ can be reached from $o_{1}$ ) if $⟨ ψ_{o_{2}} ∣ ∣ U_{a} ∣ ∣ ψ_{o_{1}} ⟩ \neq 0$ for some $a \in A$ , and take the transitive closure of this relationship. The resulting relationship is in fact also symmetric and reflexive. This follows because the unitary group is compact (since we assume $O$ is a finite and complete set of observations, so $H^{e}$ is finite dimensional), so powers of $U_{a}$ can approximate the identity and $U_{a}^{†} = U^{- 1}$ arbitrarily. Thus the MDP is a disjoint union of communicating components (the equivalence classes of the relation above). For generic ${U_{a} : a \in A}$ , we'll have a single equivalence class. Otherwise the first observation picks out a component, and the rest of the evolution remains within that component.

Theorem 7.21. If the associated MDP to a setup is communicating, then for any policy $π$ , we have $L^{*} - O (\sqrt{T log T}) \leq L^{IBP} (π),$ where $L^{*}$ is the minimal Copenhagen loss (i.e. $L^{*} = L^{Cop} (π^{*})$ for a Copenhagen-optimal policy $π^{*}$ ).

Proof. For $ϵ > 0$ , consider the event $E = {d \in D : L (d) \leq L^{*} - ϵ} .$ Choose a policy ${~ π}_{E}$ as in Definition 6.12. Then it's easy to verify using the definition of $L^{phys}$ , that $\begin{matrix} \begin{matrix} L^{phys} (π, {π, {~ π}_{E}}) \geq L^{*} - ϵ . \end{matrix} \\ (1) \end{matrix}$ Let $p = Cop (E | π)$ be the Copenhagen probability that the loss is at most $L^{*} - ϵ$ , given the policy $π$ . By Proposition 7.17 we have that $\begin{matrix} \begin{matrix} p \leq exp (- \frac{ϵ^{2}}{2 T C^{2}}) . \end{matrix} \\ (2) \end{matrix}$

By Proposition 6.18, we have $\begin{matrix} \begin{matrix} C_{E | π} \cdot δ_{π, {π, {~ π}_{E}}} \in Θ_{U}^{*}, \end{matrix} \\ (3) \end{matrix}$

for $C_{E | π} = 1 - \sqrt{p (2 - p)}$ . Therefore by $(1)$ and $(3)$ , we have $L^{IBP} = E_{Θ_{U}^{*}} [χ_{π} \cdot L^{phys}] \geq (L^{*} - ϵ) (1 - \sqrt{p (2 - p)}) .$ Here $p (2 - p) \leq 2 p$ , and using $(2)$ , we get $L^{IBP} \geq (L^{*} - ϵ) (1 - \sqrt{2} exp (- \frac{ϵ^{2}}{4 T C^{2}})) .$ To obtain an $O (\sqrt{T log T})$ bound, we can set $ϵ = C \sqrt{2 T log T}$ , which gives $L^{IBP} \geq (L^{*} - C \sqrt{2 T log T}) (1 - \sqrt{\frac{2}{T}}) = L^{*} - O (\sqrt{T log T}),$ since $L^{*} = O (T)$ . $\begin{matrix} □ \end{matrix}$

Note that Theorem 4.26 implies that any Copenhagen-optimal policy is also asymptotically IBP-optimal. The converse is also true, but requires a bit more work.

Theorem 7.22. If $¯ π$ is an IBP-optimal policy, then $L^{Cop} (¯ π) \leq L^{*} + o (T),$ where $L^{*}$ is the Copenhagen-optimal loss.

Proof. For $ϵ_{1}, ϵ_{2} > 0$ , consider the events $E_{- ϵ_{1}} = {d \in D : L (d) \leq L^{*} - ϵ_{1}},$ $E_{+ ϵ_{2}} = {d \in D : L (d) \leq L^{*} + ϵ_{2}} .$ On a high level, the proof goes as follows. We already know that the Copenhagen probability of $E_{- ϵ_{1}}$ is small. We'll show that for an IBP-optimal $¯ π$ , the complement of $E_{+ ϵ_{2}}$ also has small probability, so most of the probability mass is where the loss is between $L^{*} - ϵ_{1}$ and $L^{*} + ϵ_{2}$ , which will be sufficient to show that $L^{Cop} (¯ π)$ is not much bigger than $L^{*}$ .

Choose policies ${~ π}_{- ϵ_{1}}$ , ${~ π}_{+ ϵ_{2}}$ corresponding to $E_{- ϵ_{1}}$ and $E_{+ ϵ_{2}}$ as in Definition 6.12. Let $p_{1} = Cop (E_{- ϵ_{1}} | ¯ π),$ $p_{2} = Cop (E_{+ ϵ_{2}} | ¯ π),$ so $p_{2} \geq p_{1}$ . Again, by Proposition 6.18, $C_{- ϵ_{1}} \cdot δ_{¯ π, {¯ π, {~ π}_{- ϵ_{1}}}} \in Θ_{U}^{*},$ $C_{+ ϵ_{2}} \cdot δ_{¯ π, {¯ π, {~ π}_{+ ϵ_{2}}}} \in Θ_{U}^{*},$ where $C_{- ϵ_{1}} = 1 - \sqrt{p_{1} (2 - p_{1})},$ $C_{+ ϵ_{2}} = 1 - \sqrt{p_{2} (2 - p_{2})} .$ By Lemma 6.11, Proposition 7.24 applies as well, so in this case we also have $ρ = (C_{- ϵ_{1}} - C_{+ ϵ_{2}}) \cdot δ_{¯ π, {¯ π, {~ π}_{- ϵ_{1}}}} + C_{+ ϵ_{2}} \cdot δ_{¯ π, {¯ π, {~ π}_{+ ϵ_{2}}}} \in Θ_{U}^{*} .$ Hence $\begin{matrix} \begin{matrix} L^{IBP} (¯ π) = E_{Θ_{U}^{*}} [χ_{¯ π} \cdot L^{phys}] \geq E_{ρ} [χ_{¯ π} \cdot L^{phys}] \geq (L^{*} - ϵ_{1}) (\sqrt{p_{2} (2 - p_{2})} - \sqrt{p_{1} (2 - p_{1})}) + (L^{*} + ϵ_{2}) (1 - \sqrt{p_{2} (2 - p_{2})}) . \end{matrix} \\ (4) \end{matrix}$ Since $¯ π$ is IBP-optimal, we have for any Copenhagen-optimal policy $π^{*}$ , $\begin{matrix} \begin{matrix} L^{IBP} (¯ π) \leq L^{IBP} (π^{*}) \leq L^{Cop} (π^{*}) = L^{*} . \end{matrix} \\ (5) \end{matrix}$ From $(4)$ and $(5)$ together we have $(L^{*} - ϵ_{1}) (\sqrt{p_{2} (2 - p_{2})} - \sqrt{p_{1} (2 - p_{1})}) + (L^{*} + ϵ_{2}) (1 - \sqrt{p_{2} (2 - p_{2})}) \leq L^{*} .$ Rearranging, and using $\sqrt{p_{1} (2 - p_{1})} \leq \sqrt{2} exp (- \frac{ϵ_{1}^{2}}{4 T C^{2}})$ as before, we get $\sqrt{p_{2} (2 - p_{2})} \geq 1 - \frac{ϵ_{1} + (L^{*} - ϵ_{1}) \sqrt{2} exp (- \frac{ϵ_{1}^{2}}{4 T C^{2}})}{ϵ_{1} + ϵ_{2}},$ so choosing $ϵ_{1} = O (\sqrt{2 T log T})$ and $ϵ_{2} = O (T^{5 / 6})$ , we have $\sqrt{p_{2} (2 - p_{2})} \geq 1 - \frac{O (\sqrt{T log T})}{Θ (T^{5 / 6})} = 1 - O (\frac{\sqrt{log T}}{T^{1 / 3}}) .$ Hence $p_{2} \geq 1 - O (\frac{\sqrt[4]{log T}}{T^{1 / 6}}) .$ Therefore $L^{Cop} (¯ π) \leq p_{2} (L^{*} + ϵ_{2}) + (1 - p_{2}) O (T) \leq L^{*} + O (T^{5 / 6} \sqrt[4]{log T}) .$ $\begin{matrix} □ \end{matrix}$

We can likely improve on the exponent of $5 / 6$ via more sophisticated estimates, but we won't be needing that for the current level of our discussion.

Remark 7.23. More generally, we can see that an asymptotically Copenhagen-optimal policy is also asymptotically IBP-optimal, and vice versa. In light of Remark 7.20, this remains true even when we drop the assumption of the MDP consisting of a single communicating component. Theorems 7.21 and 7.22 can be applied to each component separately, thus the optimal policies still need to agree asymptotically. The two interpretations then weigh the asymptotic losses of the components differently based on the amplitude of the components in the initial state (the IBP interpretation is more optimistic in the sense that it typically considers the lower loss branches with more weight than the Copenhagen interpretation), hence Theorems 7.21 and 7.22 fail in the case of an initial state that is the superposition of multiple communicating components, but only due to the outcome of the first observation being irreversible in this case, which doesn't affect the claim about the optimal policies agreeing asymptotically.

We finish this section by spelling out the proof of the following.

Proposition 7.24. If $π, π_{1}, π_{2}$ are three policies such that for any $B \in U$ , $E_{β_{B} (π) \land β_{B} (π_{1})} [1] \geq C_{1},$ $E_{β_{B} (π) \land β_{B} (π_{2})} [1] \geq C_{2},$ for $C_{1} \geq C_{2}$ , then $ρ = (C_{1} - C_{2}) \cdot δ_{π, {π, π_{1}}} + C_{2} \cdot δ_{π, {π, π_{2}}} \in Θ_{U}^{*} .$

Proof. The proof is mostly analogous to Proposition 6.18, we highlight the additional ideas here. The claim reduces to Proposition 6.18 for $C_{1} = C_{2}$ , so we'll assume $C_{1} > C_{2}$ in the following. For $B \in U$ , let (cf. Definition 6.14) ${¯ ϕ}_{2 B} = β_{B} (π) \land β_{B} (π_{2}),$ $ϕ_{2 B} = \frac{C_{2}}{E_{{¯ ϕ}_{2 B}} [1]} {¯ ϕ}_{2 B},$ so $E_{ϕ_{2 B}} [1] = C_{2}$ , and $ϕ_{2 B} \leq {¯ ϕ}_{2 B} \leq β_{B} (π_{2})$ , since $E_{{¯ ϕ}_{2 B}} [1] \geq C_{2}$ by assumption. Now let ${¯ ϕ}_{1 B} = (β_{B} (π) - ϕ_{2 B}) \land β_{B} (π_{1}),$ $ϕ_{1 B} = \frac{C_{1} - C_{2}}{E_{{¯ ϕ}_{1 B}} [1]} {¯ ϕ}_{1 B},$ so $E_{ϕ_{1 B}} [1] = C_{1} - C_{2}$ , and $ϕ_{1 B} \leq {¯ ϕ}_{1 B} \leq β_{B} (π_{1})$ , since $E_{{¯ ϕ}_{1 B}} [1] \geq C_{1} - C_{2}$ by the assumption that $E_{β_{B} (π) \land β_{B} (π_{1})} [1] \geq C_{1}$ . Moreover, by construction $ϕ_{1 B} + ϕ_{2 B} \leq β_{B} (π)$ . We can then define for any finite $F \subset U$ , $ϕ_{1 F} = \frac{1}{(C_{1} - C_{2})^{| F | - 1}} \prod B \in F ϕ_{1 B} \in Δ^{c} Φ_{F},$ $ϕ_{2 F} = \frac{1}{C_{2}^{| F | - 1}} \prod B \in F ϕ_{2 B} \in Δ^{c} Φ_{F},$ so analogously to Lemma 6.16, we have $ϕ_{1 F} \in β_{F} (π_{1}),$ $ϕ_{2 F} \in β_{F} (π_{2}),$ $ϕ_{1 F} + ϕ_{2 F} \in β_{F} (π) .$ Using this, we can show that $\begin{matrix} θ_{F} = δ_{π, {π, π_{1}}} \times ϕ_{1 F} + δ_{π, {π, π_{2}}} \times ϕ_{2 F} \in Br (Θ_{F}) \subset Δ^{c} ({el}^{Γ} \times Φ_{F}) . \end{matrix}$

To see this, consider an endomorphism $s : Γ \to Γ$ , and let $~ s$ be as in Definition 3.12. The interesting cases are the following:

If $s (π) = π$ , then $~ s (θ_{F}) = δ_{π} \times (ϕ_{1 F} + ϕ_{2 F}) \in Θ_{F},$ since $ϕ_{1 F} + ϕ_{2 F} \in β_{F} (π)$ by the above.
If $s (π) = π_{i}$ for $i = 1, 2$ , then $~ s (θ_{F}) = δ_{π_{i}} \times ϕ_{i F} \in Θ_{F},$ since $ϕ_{i F} \in β_{F} (π_{i})$ as well by the above.

Therefore ${pr}_{*} (θ_{F}) = ρ \in Θ_{F}^{*} .$ Since this is true for arbitrary $F$ , we conclude $ρ \in Θ_{U}^{*}$ . $\begin{matrix} □ \end{matrix}$

8. Limitations

We mention some limitations of the setting, some of which as simply due to the toy nature of the model, others seem to be more inherent to infra-Bayesian physicalism.

8.1. Limitations of the toy setting

Although a central feature of infra-Bayesian physicalism is a lack of privilege for any observer, in the toy model we work with an explicit decomposition of the universe into agent and environment. Other toy assumptions are taking the "computational universe" $Γ$ to consist solely of the policy, and the explicit dependence of the time evolution on the policy. In a more realistic setting we would start with a non-Cartesian (not agent-centric) description of the universe, and a rich nexus of mathematical structure encoded in $Γ$ . The entanglement between the agent's policy and the physical state of the universe would then be encoded implicitly via a "theory of origin" whereby the agent arises in the given universe.

To spell the above out a little more, in a more realistic setting we could take $Σ = {⊤, ⊥}$ , and choose $R$ to be a sufficiently rich set of computations to include things like

$r =$ "a program computing the 11th decimal place digit of the amplitude squared of a certain path integral in some lattice QFT and verifying if it’s equal to 7".

Then $Γ = Σ^{R}$ will contain a lot of immediately inconsistent valuations, like the one where a certain digit is both equal to 7 and to 3. However, we can take a subset $Γ_{0} \subset Γ$ , which is "consistent enough", e.g. so that for every computation of the form "a certain digit in a given quantity equals $i$ ", exactly one of $i \in {0, \dots, 9}$ evaluates to $⊤$ , all others evaluate to $⊥$ . We would choose $Γ_{0}$ to be sufficiently small to produce a meaningful map $β : Γ_{0} \to □ Φ$ (describing a certain model of physics), e.g. so that the distribution of the momentum of a given field modeled in $Φ$ , at a point is given as specified by the values of the computations like $r$ above. We can then combine the mathematical/computational part of a hypothesis $Θ_{Γ} \in □ Γ$ (supported only on the sufficiently consistent part of the computational universe $Γ_{0} \subset Γ$ ) with $β$ to construct a corresponding joint hypothesis $Θ = Θ_{Γ} ⋉ β \in □ (Γ \times Φ)$ .

The notion of a "theory of origin" has not been formalized yet, but we informally discuss some ingredients here. Given the source code $G$ of the agent, and a policy $π$ , we can define the $π$ -counterfactual of $Θ$ as $Θ^{π} = ({pr}_{{el}^{Γ}})_{*} (Br (Θ)) \cap ⊤_{C^{π}} \in □ {el}^{Γ},$ where $C^{π}$ is the subset of universes compatible (by some notion) with the given policy $π$ (cf. [IBP Definition 1.5], also Remark 4.23). We can then look at the diameter of these counterfactuals in some metric, $diam ({Θ^{π} : π : O^{*} \to A}),$ as a measure of the extent to which the agent is realized in the given physical model (i.e. how entangled the agent's policy is with the world). Moreover, in a more realistic setting we would expect the entanglement between the policy and the world to come from "non-contrived" reasons (as opposed to our toy model, where we just postulated the dependence of the time evolution on the policy), which could be measured by some notion of complexity of the source code $G$ relative to the physical hypothesis $β$ (higher relative complexity means a less contrived theory of origin).

8.2. Limitations of the broader framework

The decision theory of infra-Bayesian physicalism is based on a computationalist loss function $L : {el}^{Γ} \to R_{\geq 0}$ . So the value of the loss is required to be determined by the state of the computational universe plus the fact of which computations are realized in the physical universe. This can lead to non-trivial translation problems from loss functions that are specified in more traditional terms. Moreover, the computationalist loss function is required to be monotonic (see monotonicity principle in [IBP]) in the computations realized, a requirement not immediately intuitive.

Working with a finite time horizon is convenient for technical reasons, but not expected to be strictly necessary. ↩︎
Richard Durrett. Probability: theory and examples. Duxbury Press, second edition, 1996. ↩︎
Veronika Baumann and Časlav Brukner. Wigner’s friend as a rational agent, 2019. ↩︎
If we wanted to work in a strictly subjectivist framework for the friend, we could include an additional observation of Wigner's memory tape by the friend, and have the loss function depend on the outcome of that observation. We don't expect this to make a significant difference for the present discussion. ↩︎
We could also require that $α$ witness $F$ having observed something, which would correspond to adding the condition that $(\forall ~ γ \in α : {~ γ}^{F} (o_{0}) = γ^{F} (o_{0})) or (\forall ~ γ \in α : {~ γ}^{F} (o_{1}) = γ^{F} (o_{1}))$ . We expect this would change some of the exact expected values of the loss, but not the optimal policy in this case. ↩︎
Martin L. Puterman. Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley & Sons, Inc., 1st edition, 1994 ↩︎ ↩︎ ↩︎ ↩︎

^{^}

Note that de Blanc's proposal is inapplicable here, since the quantum ontology is not a Markov decision process.

^{^}

To be clear, this is just a vague informal description, FCR is an actual rigorous mathematical framework.

^{^}

Note that de Blanc's proposal is inapplicable here, since the quantum ontology is not a Markov decision process.

^{^}

To be clear, this is just a vague informal description, FCR is an actual rigorous mathematical framework.

[-]Vanessa Kosoy3moΩ9210Review for 2024 Review

The interpretation of quantum mechanics is a philosophical puzzle that was baffling physicists and philosophers for about a century. In my view, this confusion is a symptom of us lacking a rigorous theory of epistemology and metaphysics. At the same time, creating such a theory seems to me like a necessary prerequisite for solving the technical AI alignment problem. Therefore, once we created a candidate theory of metaphysics (Formal Computation Realism (FCR), formerly known as infra-Bayesian Physicalism), the interpretation of quantum mechanics stood out as a powerful test case. In the work presented in this post, we demonstrated that FCR indeed passes this test (at least to a first approximation).

What is so confusing about quantum mechanics? To understand this, let's take a look at a few of the most popular pre-existing interpretations.

The Copenhagen Interpretation (CI) proposes a mathematical rule for computing the probabilities of observation sequences, via postulating the collapse of the wavefunction. For every observation, you can apply the Born Rule to compute the probabilities of different results, and once a result is selected, the wavefunction is "collapsed" by projecting it to the corresponding eigenspace.

CI seems satisfactory to a logical positivist: if all we need from a physical theory is computing the probabilities of observations, we have it. However, this is unsatisfactory for a decision-making agent if the agent's utility function depends on something other than its direct observations. For such an agent, CI offers no well-defined way to compute expected utility. Moreover, while normally decoherence ensures that the observations of all agents are in some sense "consistent", in principle it is theoretically possible to create a situation in which decoherence fails and CI will prescribe contradictory beliefs to different agents (as in the Wigner's friend thought experiment).

In CI, the wavefunction is merely a book-keeping device with no deep meaning of its own. In contrast, the Many Worlds Interpretation (MWI) takes a realist metaphysical stance, postulating that the wavefunction describes the objective physical state of the universe. This, in principle, admits meaningful unobservable quantities on which the values of agents can depend. However, the MWI has no mathematical rule for computing probabilities of observation sequences. If all "worlds" exist at the same time, there's no obvious reason to expect to see one of them rather than another. MWI proponents address this by handwaving into existence some "degree of reality" that some worlds posses more than others. However, the fundamental fact remains that there is no well-defined prescription for probabilities of observation sequences, unless we copy the prescription of CI: however the latter is inconsistent with the intent of MWI in cases when decoherence fails, such as Wigner's friend.

In principle, we can defend an MWI-based decision-theory in which the utility function is a self-adjoint operator on the Hilbert space and we are maximizing its expectation in the usual quantum-mechanical sense. Such a decision-theory can avoid the need for a well-defined probability distribution over observation sequences. However, it would leave us with an "ontological crisis": if our agent did not start out knowing quantum mechanics, how would it translate its values into this quantum mechanical form?^[1]

The De Broglie-Bohm Interpretation (DBBI) proposes that in addition to the wavefunction, we should also postulate a classical trajectory following a time-evolution law that depends on the wavefunction. This results in a realist theory with a well-defined distribution over observation sequences. However, it comes with two major issues:

The observations have to be a function of the positional variables only (and not of the momenta variables). This is probably false even for humans and hardly applicable for arbitrary agents.
The theory is not Lorentz invariant. This is disturbing in and of itself, but in particular it implies that e.g. the experiences of humans moving at relativistic speeds compared to the preferred frame of reference (whatever that is) are devoid of value (i.e. such humans apparently have no qualia), if we circumvented problem #1 somehow.

In my view, the real source of all the confusion is the lack of rigorous metaphysics: we didn't know (prior to this line of research), in full generality, what the type signature of a physical theory should be and how should we evaluate such a theory.

Enter Formal Computational Realism (FCR). According to FCR, the fundamental ontology in which all beliefs and values about the world should be expressed is computable logical facts plus the computational information content of the universe. The universe can contain information about computations (e.g., if someone calculated the 700th digit of pi, then the universe contains this information), and fundamentally this information is all there is^[2]. Moreover, given an algorithmic description of a physical theory plus the epistemic state of an agent in relation to computable logical facts, it is possible to formally specify the computational information content that this physical theory implies, from the perspective of the agent. The latter operation is called the "bridge transform".

To apply this to quantum mechanics, we need to choose a particular algorithmic description. The choice we settled on is fairly natural: We imagine all possible quantum observables as having marginal distributions that obey the Born rule, with the joint distribution being otherwise completely ambiguous (in the sense that imprecise probability allows distributions to be ambiguous, i.e. we have "Knightian uncertainty" about it). The latter is a natural choice, because quantum mechanics has no prescription for the joint distribution of noncommuting observables. The combined values of all observables is the "state" that the physical theory computes, and the agent's policy is treated as an unknown logical fact on which the computation depends.

Applying the bridge transform to the above operationalization of quantum mechanics, we infer the computational information content of the universe according to quantum mechanics, and then use the latter to extract the probabilities of various agent experiences. What we discover is as follows:

As in MWI, multiple copies of the agent experiencing different "Everett branches" can coexist.
Unlike MWI, not all Everett branches are instantiated, but only some (according to some well-defined probability distribution).
Assuming decoherence, the probability distribution is s.t. from the perspective of any copy of the agent, the universe seems to obey CI probabilities. That is, any statistical test that the agent can run will converge to confirming the CI distribution in the limit with probability 1, for all copies of the agent.
As opposed to CI, all agents have "consistent" expectations even when decoherence fails. We haven't fully formalized this claim, but it seems clear from the general nature of FCR, and we did it investigate it in the specific example of Wigner's friend.

As opposed to most pre-existing interpretations, the resulting formalism has precisely defined decision-theoretic prescriptions for an agent in any "weird" (i.e. not-decohering) situation like e.g. Wigner's friend. This only requires the agent's values to be specified in the FCR ontology (and in particular allows the agent to assign value to their own experiences, in some arbitrary history-dependent way, and/or the experiences of particular other agents).

In conclusion, FCR passed a non-trivial test here. It was not obvious to me that it would: before Gergely figured out the details, I wasn't sure that it's going to work at all. As such, I believe this to be a milestone result. (With some caveats: e.g. it needs to be rechecked for the non-monotonic version of the framework.)

^{^}
Note that de Blanc's proposal is inapplicable here, since the quantum ontology is not a Markov decision process.
^{^}
To be clear, this is just a vague informal description, FCR is an actual rigorous mathematical framework.

[-]Algon2mo20

We imagine all possible quantum observables as having marginal distributions that obey the Born rule

Dumb question, but does this approach of yours cash out to representing quantum states as a probability distribution function? How's this rich enough to represent interference of states and all that quantum phenomena absent from stochastic dynamics?

[-]Vanessa Kosoy2mo40

Strictly speaking, there's no result saying you can't represent quantum phenomena by stochastic dynamics (a.k.a. hidden variables). Indeed, e.g. the de Broglie-Bohm interpretation does exactly that. What does exist is Bell's inequality, which implies that it's impossible to represent quantum phenomena by local hidden variables (local = the distribution is the limit of causal graphs in which variables are localized in spacetime and causal connections only run along future-directed timelike (not superluminal) separations). Now, our framework doesn't even fall in the domain of Bell's inequality, since (i) we have supracontributions (in this post called "ultracontributions") instead of ordinary probability distributions (ii) we have multiple co-existing "worlds". AFAIK, Bell-inequality-based arguments against local hidden variables support neither i nor ii. As such, it is conceivable that our interpretation is in some sense "local". On the other hand, I don't know that it's local and have no strong reason to believe it.

[-]TAG2mo00

>The interpretation of quantum mechanics is a philosophical puzzle that was baffling physicists and philosophers for about a century. In my view, this confusion is a symptom of us lacking a rigorous theory of epistemology and metaphysics

They are symptoms of each other. Epistemology depends on ontology, ontology depends on the right interpretation of physics...which depends on epistemology.

>What is so confusing about quantum mechanics?

Recovering the appearance of a classical reality from a profoundly unclassical substructure.

>and CI will prescribe contradictory beliefs to different agents (as in the Wigner’s friend thought experiment).

It's important to notice that Wigners Friend only implies an inconsistency about when collapse occurred: there is no inconsistency between what Wigner and the Friend actually measure. So CI is still consistent as an instrumentalist theory. Indeed, you can cast it as an instrumentalist theory, by refusing to speak about collapse as a real process, and only requiring that observers make sharp real-valued observations for some unknown reason -- substituting an irrealist notion of measurement for collapse.

>In CI, the wavefunction is merely a book-keeping device with no deep meaning of its own. In contrast

If you are going to be realist about collapse, you need to be realist about WF's -- otherwise what is collapsing? Realism about both is consistent, irrealism about both is consistent.

>However, the MWI has no mathematical rule for computing probabilities of observation sequences. If all “worlds” exist at the same time, there’s no obvious reason to expect to see one of them rather than another. MWI proponents address this by handwaving into existence some “degree of reality” that some worlds posses more than others. However, the fundamental fact remains that there is no well-defined prescription for probabilities of observation sequences, unless we copy the prescription of CI: however the latter is inconsistent with the intent of MWI in cases when decoherence fails, such as Wigner’s friend.

"The" MWI is more than one thing. If you are talking about coherent superposition, then there is no need to invent a probabilistic weighting , since standard quantum mechemical measure (WF amplitude) gives you that via the Born rule. But we can tell.we are not in a macroscopic coherent superposition, because it would look weird. If you are talking about decoherent branching, it's not clear how or whether branches are weighted. That might matter for the purposes of physics, since the experimenter is only operating in one branch, and any other can have no effect. But for some other purposes , such as large world ethics, or anthropics, it might be nice to have weights for branches.

>and fundamentally this information is all there is

If you want to do decision theory, and not just probability theory , you need ontology, not just epistemology. But why would the process stop there? Is decision theory the most ambitious goal you can have?

Most of the current debate about metaphysics centres on consciousness. Physicalism, of a substantial kind, materialism, seems unable to explain phenomenal consciousness -- why should an insubstantial, information-only ontology fare any better? Rather than having anything extra to offer, it is more minimal. The same information can appear in different forms .. drinking the wine is not reading the label .. which is a strong hint that information is not there is.

[-]Mitchell_Porter2y20

Wouldn't an infra-Bayesian formalization be possible for any interpretation (whether ontological or epistemological) that is mathematically precise?

[-]Yegreg2y10

What do you mean by a mathematically precise interpretation? And what would it mean to have an infra-Bayesian formalization of any such interpretation?

What do you mean by a mathematically precise interpretation?

A mathematically precise ontological interpretation is one in which all the elementary properties of all the world(s) are unambiguously specified. A many-worlds example would be a Hartle multiverse in which histories are specified by a particular coarse-grained selection of observables. A one-world example would be a Bohmian universe with a definite initial condition and equation of motion.

A mathematically precise epistemological interpretation is one in which reality is divided into agent and environment, and e.g. the wavefunction is interpreted as implying subjective probabilities, likelihoods of possible experiences, and so forth.

what would it mean to have an infra-Bayesian formalization of any such interpretation?

My understanding of infra-Bayesianism is not as precise as I would wish, but isn't it basically a kind of decision theory that can apply within various possible worlds? So this would mean, implementing infra-Bayesian decision theory within the worlds of the interpretations above.

Thanks for clarifying. I'll try to answer the original question first, and then expand a little on the comparison with other interpretations that might help understand the motivation for this work a little better.

I'm imagining on the high level you have something like the following in mind (correct me if not). Suppose is all the possible states of the universe, and suppose we have a subset of possible worlds (the "multiverse") $M \subset Φ$ , then we might simply say we have Knightian uncertainty over the possible worlds, which would correspond to an infra-belief $Θ = ⊤_{M} \in □ Φ$ . Then if we have a loss function $L : Φ \to R$ , we might apply some decision rule, e.g. minimizing worst-case expected loss ${max}_{θ \in Θ} E_{θ} [L]$ (note that in this case this just turns out to be ${max}_{m \in M} L (m)$ ). Arguably, this is not a very good way to make decisions in a quantum multiverse, since we're completely ignoring the amplitudes of the different worlds.

The usual thing to do instead is to consider the distribution $θ_{M} = \sum_{m \in M} p_{m} m \in Δ Φ$ , where the probability $p_{m} = | α_{m} |^{2}$ , assuming $M$ is a decoherent set of worlds, and $α_{m}$ is the amplitude of world $m$ . Then we can consider minimizing the expected loss $E_{θ_{m}} [L]$ . Putting aside questions of subjective versus objective probabilities (and what the latter would mean), this high-level approach could cover various ontological interpretations, including the Bohmian view, and consistent histories (which is what Hartle uses).

I would say the main issue with the above approach is that it involves a choice of ontology $Φ$ as well as a choice of multiverse $M$ (note that these are both things that an agent inside the universe would construct). Even if we assumed that we do have a loss function $L : Φ \to R$ (which is already very questionable), the expected loss in general would still depend on the choice of the multiverse.

Infra-Bayesian physicalism is aiming to address some of these issues by providing a framework to talk about losses that translate meaningfully across ontologies.

Hello again. I regret that so much time has passed. My problem seems to be that I haven't yet properly understood everything that goes into the epistemology and decision-making of an infra-bayesian agent.

For example, I don't understand how this framework "translates across ontologies". I would normally think of ontologies as mutually exclusive possibilities, which can be subsumed into a larger framework by having a broad notion of possibility which includes all the ontologies as particular cases. Does the infra-bayesian agent think in some other way?

[-]Yegreg2y30

I would say the translation across ontologies is carried out by "computationalism" in this case, rather than infra-Bayesianism itself. That is, (roughly speaking) we consider which computations are instantiated in various ontologies, and base our loss function off of that. From this viewpoint infra-Bayesianism comes in as an ingredient of a specific implementation of computationalism (namely, infra-Bayesian physicalism). In this perspective the need for infra-Bayesianism is motivated by the fact that an agent needs to have Knightean uncertainty over part of the computational universe (e.g. the part relating to its own source code). Let me know if this helps clarify things.

LESSWRONG
LW

LESSWRONG
LW

34

Interpreting Quantum Mechanics in Infra-Bayesian Physicalism

34

Ω 19

Abstract

1. Introduction

1.1. Discussion of the results

1.2. Outline

2. Setup

3. Prerequisites

3.1. Ultracontributions

3.2. Some constructions

3.3. The bridge transform

4. An infra-Bayesian physicalist interpretation

4.1. Copenhagen interpretation

4.2. Relating the two interpretations

4.3. Decision theory

5. Examples

5.1. Counterexamples

5.2. Wigner's friend

6. Bounds on the ultraprobabilities

6.1. Upper bound

6.2. Lower bound

7. Asymptotic convergence

7.1. Upper bound

7.2. Asymptotic behavior of communicating MDPs

7.3. Lower bound

8. Limitations

8.1. Limitations of the toy setting

8.2. Limitations of the broader framework

34

Ω 19

34

Ω 19