Comment Permalink

Matt Vincent1mo20

typically don't interact non-trivially

Or, as Orwell would prefer, "typically interact trivially".

See in context

282 So You Want To Make Marginal Progress...

by johnswentworth

7th Feb 2025

5 min read

282

Once upon a time, in ye olden days of strange names and before google maps, seven friends needed to figure out a driving route from their parking lot in San Francisco (SF) down south to their hotel in Los Angeles (LA).

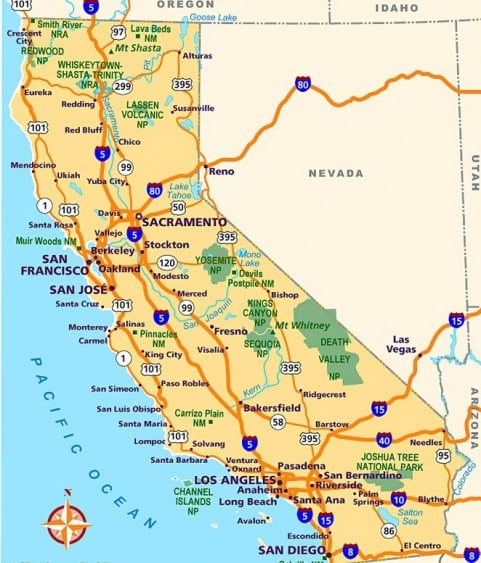
The first friend, Alice, tackled the “central bottleneck” of the problem: she figured out that they probably wanted to take the I-5 highway most of the way (the blue 5’s in the map above). But it took Alice a little while to figure that out, so in the meantime, the rest of the friends each tried to make some small marginal progress on the route planning.

The second friend, The Subproblem Solver, decided to find a route from Monterey to San Louis Obispo (SLO), figuring that SLO is much closer to LA than Monterey is, so a route from Monterey to SLO would be helpful. Alas, once Alice had figured out that they should take I-5, all The Subproblem Solver’s work was completely useless, because I-5 dodges the whole Monterey-to-SLO area entirely.

The third friend, The Forward Chainer, started from the parking lot in San Francisco and looked for a route which would generally just go south and a little east, toward LA, whenever possible. Alas, once Alice figured out that they should take I-5, The Forward Chainer’s work was completely useless, because it turned out that the fastest strategy was to head east from San Francisco (toward I-5), rather than south.

The fourth friend, The Backward Chainer, started from their hotel in LA and looked for a route which would generally just go north and a little west, toward San Francisco. Alas, this turned out to be completely useless in much the same way as The Forward Chainer’s work… though by dumb luck it was a “near miss”, in some sense, as only a few routes looked better than the I-5 by The Backward Chainer’s “go north and west from hotel” criterion.

The fifth friend, The Very General Helper, bought snacks for the trip. Snacks are great no matter the route. Everybody likes The Very General Helper, she’s great.

The sixth friend, The Clever One, realized that they’d probably need to stop for gas along the way, so she found a gas station about halfway between SF and LA. It was in Paso Robles, near the coast. Alas, once Alice figured out that they should take I-5, The Clever One’s work was also completely useless. The friends just found a different gas station on I-5 rather than make a detour all the way out to Paso Robles.

The seventh friend, The One Who Actually Thought This Through A Bit, realized upfront that once Alice figured out the main route, it would totally change all the subproblems her friends were tackling. So, she squinted at a map a bit, trying to figure out if there was any particular subproblem which would predictably generalize - a subproblem which would be useful to solve for any (or at least most) plausible choices made by Alice, without having to know in advance what main route Alice would go with. And she realized that the mountains just north of LA only had a couple easy passes through them - one for I-5, and another out by the coast (route 1). So, she tried to figure out routes from both I-5 and route 1 to their hotel in LA. Her work turned out to be useful: as soon as Alice figured out that they needed to take I-5 most of the way, The One Who Actually Thought This Through A Bit promptly offered a route from I-5 to their hotel in LA.

The Generalizable Lesson

Making marginal progress on a problem, i.e. tackling a non-bottlenecking subproblem, has a hidden extra requirement: a solution must generalize to work well with the whole wide class of possible solutions to other subproblems (especially the main bottleneck).

When tackling the bottleneck itself, one does not need to worry as much about this generalization requirement. Why? Well, the whole point of a “bottleneck” is that it’s the main hard/costly part; we’re perfectly happy to make other subproblems more difficult (on the margin) in exchange for solving the main bottleneck. So if a solution to the main bottleneck plays poorly with solutions to other subproblems, whatever, it’s cheaper to go find new solutions to those other subproblems than a new solution to the bottleneck.

But when solving a non-bottleneck problem, we have no such “out”. Solutions to our subproblem must generalize enough to work with solutions to other subproblems. And that’s a pretty tricky constraint, when we don’t already know how to solve the main bottleneck(s).

Application: <Your Research Field>

So let’s say you’re working on <your research field here>^[1]. You don’t fancy yourself one of the greatest minds in the field, you’re just trying to make a marginal contribution.

… alas, in this specific way your challenge is actually harder than solving the big hard central problems. Because your marginal contribution needs to be sufficiently generalizable to play well with whatever techniques are ultimately used to solve the big hard central problems… and you have no idea what those techniques might be. Indeed, probably one of the main reasons you’re aiming for a marginal contribution in the first place is to avoid needing to worry about those big hard central problems.

So you have basically two options, corresponding to The Very General Helper and The One Who Actually Thought This Through A Bit in the parable above.

The Very General Helper strategy: find a way to contribute which will be helpful no matter how the big hard central problems are solved. Remember that big hard problems are often solved in Weird Ways totally orthogonal to anything you ever considered, so your contribution had better be very robustly generalizably valuable.
The One Who Actually Thought This Through A Bit strategy: think through the big hard central problems enough to find some predictable aspect of them, some particular subproblem which will come up no matter how the big hard central problems are solved. Again, remember that big hard problems are often solved in Weird Ways totally orthogonal to anything you ever considered, so you better be very sure your subproblem will robustly and generalizably show up as a subproblem of any solution to the big hard central problems.

Notice the theme in both of these: robust generalization. If you do not choose robustly generalizable subproblems and find robustly generalizable solutions to them, then most likely, your contribution will not be small; it will be completely worthless. Once the bottleneck problems are sorted out, the problem will predictably look very different, because that’s what happens when a bottleneck is handled; your subproblem and solution need to generalize to that very different scenario in order to actually be useful.

^{^}
Ok, fine, it's AI alignment/safety.

Intellectual Progress (Individual-Level)Intellectual Progress (Society-Level)World ModelingRationality

Curated

282

Mentioned in

10Musings on Scenario Forecasting and AI

New Comment

42 comments, sorted by

top scoring

Click to highlight new comments since: Today at 5:15 PM

[-]ryan_greenblatt2mo*10833

This post seems to assume that research fields have big, hard central problems that are solved with some specific technique or paradigm.

This isn't always true. Many fields have the property that most of the work is on making small components work slightly better in ways that are very interoperable and don't have complex interactions. For instance, consider the case of making AIs more capable in the current paradigm. There are many different subcomponents which are mostly independent and interact mostly multiplicatively:

Better training data: This is extremely independent: finding some source of better data or better data filtering can be basically arbitrarily combined with other work on constructing better training data. That's not to say this parallelizes perfectly (given that work on filtering or curation might obsolete some prior piece of work), but just to say that marginal work can often just myopically improve performance.
Better architectures: This breaks down into a large number of mostly independent categories that typically don't interact non-trivially:
- All of attention, MLPs, and positional embeddings can be worked on independently.
- A bunch of hyperparameters can be better understood in parallel
- Better optimizers and regularization (often insights within a given optimizer like AdamW can be mixed into other optimizers)
- Often larger scale changes (e.g., mamba) can incorporate many or most components from prior architectures.
Better optimized kernels / code
Better hardware

Other examples of fields like this include: medicine, mechanical engineering, education, SAT solving, and computer chess.

I agree that paradigm shifts can invalidate large amounts of prior work (and this has occurred at some point in each of the fields I list above), but it isn't obvious whether this will occur in AI safety prior to human obsolescence. In many fields, this doesn't occur very often.

[-]johnswentworth2mo3914

This post seems to assume that research fields have big hard central problems that are solved with some specific technique or paradigm.
This isn't always true. [...]

I would say it is basically-always true, but there are some fields (including deep learning today, for purposes of your comment) where the big hard central problems have already been solved, and therefore the many small pieces of progress on subproblems are all of what remains.

And insofar as there remains some problem which is simply not solvable within a certain paradigm, that is a "big hard central problem", and progress on the smaller subproblems of the current paradigm is unlikely by-default to generalize to whatever new paradigm solves that big hard central problem.

I agree that paradigm shifts can invalidate large amounts or prior work, but it isn't obvious whether this will occur in AI safety.

I claim it is extremely obvious and very overdetermined that this will occur in AI safety sometime between now and superintelligence. The question which you'd probably find more cruxy is not whether, but when - in particular, does it come before or after AI takes over most of the research?

... but (I claim) that shouldn't be the cruxy question, because we should not be imagining completely handing off the entire alignment-of-superintelligence problem to early transformative AI; that's a recipe for slop. We ourselves need to understand a lot about how things will generalize beyond the current paradigm, in order to recognize when that early transformative AI is itself producing research which will generalize beyond the current paradigm, in the process of figuring out how to align superintelligence. If an AI assistant produces alignment research which looks good to a human user, but won't generalize across the paradigm shifts between here and superintelligence, then that's a very plausible way for us to die.

[-]ryan_greenblatt2mo252

I would say it is basically-always true, but there are some fields (including deep learning today, for purposes of your comment) where the big hard central problems have already been solved, and therefore the many small pieces of progress on subproblems are all of what remains.

Maybe, but it is interesting to note that:

A majority of productive work is occuring on small subproblems even if some previous paradigm change was required for this.
For many fields, (e.g., deep learning) many people didn't recognize (and potentially still don't recognize!) that the big hard central problem was already solved. This potentially implies it might be non-obvious whether this has been solved and making bets on some existing paradigm which doesn't obviously suffice can be reasonable.

Things feel more continuous to me than your model suggests.

And insofar as there remains some problem which is simply not solvable within a certain paradigm, that is a "big hard central problem", and progress on the smaller subproblems of the current paradigm is unlikely by-default to generalize to whatever new paradigm solves that big hard central problem.

It doesn't seem clear to me this is true in AI safety at all, at least for non-worst-case AI safety.

I claim it is extremely obvious and very overdetermined that this will occur in AI safety sometime between now and superintelligence.

Yes, I added "prior to human obsolescence" (which is what I meant).

Depending on what you mean by "superintelligence", this isn't at all obvious to me. It's not clear to me we'll have (or will "need") new paradigms before fully handing over all technical and strategic work to AIs which are capable enough to obsolete humans at all cognitive tasks. Doing this hand over doesn't directly require understanding whether the AI is specifically producing alignment work that generalizes. For instance, the system might pursue routes other than alignment work and we might determine its judgement/taste/epistimics/etc are good enough based on examining things other than alignment research intended to generalize beyond the current paradigm.

If by superintelligence, you mean wildly superhuman AI, it remains non-obvious to me that new paradigms are needed (though I agree they will pretty likely arise prior to this point due to AIs doing vast quantity of research if nothing else). I think thoughtful and laborious implementation of current paradigm strategies (including substantial experimentation) could directly reduce risk from handing off to superintelligence down to perhaps 25% and I could imagine being argued considerably lower.

[-]johnswentworth2mo1212

It's not clear to me we'll have (or will "need") new paradigms before fully handing over all technical and strategic work to AIs which are capable enough to obsolete humans at all cognitive tasks.

If you want to not die to slop, then "fully handing over all technical and strategic work to AIs which are capable enough to obsolete humans at all cognitive tasks" not a thing which happens at all until the full superintelligence alignment problem is solved. That is how you die to slop.

[-]ryan_greenblatt2mo90

"fully handing over all technical and strategic work to AIs which are capable enough to obsolete humans at all cognitive tasks"

Suppose we replace "AIs" with "aliens" (or even, some other group of humans). Do you agree that doesn't (necessarily) kill you due to slop if you don't have a full solution to the superintelligence alignment problem?

[-]johnswentworth2mo137

Aliens kill you due to slop, humans depend on the details.

The basic issue here is that the problem of slop (i.e. outputs which look fine upon shallow review but aren't fine) plus the problem of aligning a parent-AI in such a way that its more-powerful descendants will robustly remain aligned, is already the core of the superintelligence alignment problem. You need to handle those problems in order to safely do the handoff, and at that point the core hard problems are done anyway. Same still applies to aliens: in order to safely do the handoff, you need to handle the "slop/nonslop is hard to verify" problem, and you need to handle the "make sure agents the aliens build will also be aligned, and their children, etc" problem.

[-]johnswentworth2mo100

If by superintelligence, you mean wildly superhuman AI, it remains non-obvious to me that new paradigms are needed (though I agree they will pretty likely arise prior to this point due to AIs doing vast quantity of research if nothing else). I think thoughtful and laborious implementation of current paradigm strategies (including substantial experimentation) could directly reduce risk from handing off to superintelligence down to perhaps 25% and I could imagine being argued considerably lower.

I find it hard to imagine such a thing being at all plausible. Are you imagining that jupiter brains will be running neural nets? That their internal calculations will all be differentiable? That they'll be using strings of human natural language internally? I'm having trouble coming up with any "alignment" technique of today which would plausibly generalize to far superintelligence. What are you picturing?

[-]ryan_greenblatt2mo100

I think you might first reach wildly superhuman AI via scaling up some sort of machine learning (and most of that is something well described as deep learning). Note that I said "needed". So, I would also count it as acceptable to build the AI with deep learning to allow for current tools to be applied even if something else would be more competitive.

(Note that I was responding to "between now and superintelligence", not claiming that this would generalize to all superintelligences built in the future.)

I agree that literal jupiter brains will very likely be built using something totally different than machine learning.

[-]johnswentworth2mo62

Yeah ok. Seems very unlikely to actually happen, and unsure whether it would even work in principle (as e.g. scaling might not take you there at all, or might become more resource intensive faster than the AIs can produce more resources). But I buy that someone could try to intentionally push today's methods (both AI and alignment) to far superintelligence and simply turn down any opportunity to change paradigm.

[-]Ariel_1mo80

Other examples of fields like this include: medicine, mechanical engineering, education, SAT solving, and computer chess.

To give a maybe helpful anecdote - I am a mechanical engineer (though I now work in AI governance), and in my experience that isnt true at least for R&D (e.g. a surgical robot) where you arent just iterating or working in a highly standardized field (aerospace, hvac, mass manufacturing etc). The "bottleneck" in that case is usually figuring out the requirements (e.g. which surgical tools to support? whats the motion range, design envelope for interferences). If those are wrong, the best design will still be wrong.

In more standardized engineering fields the requirements (and user needs) are much better known, so perhaps the bottleneck now becomes a bunch of small things rather than one big thing.

[-]ryan_greenblatt1mo21

Importantly, this is an example of developing a specific application (surgical robot) rather than advancing the overall field (robots in general). It's unclear whether the analogy to an individual application or an overall field is more appropriate for AI safety.

[-]Ariel_1mo20

Good point. Thinking of robotics overall, it's much more of a bunch of small stuff than one big thing. Though it depends how far you "zoom out" I guess. Technically Linear Algebra itself, or the Jacobian, is an essential element of robotics. But could also zoom in on a different aspect and then say that "zero backlash gearboxes" (where Harmonic Drive is notable as it's much more compact and accurate than prev versions - but perhaps a still small effect in the big picture) are the main element. Or PID control, or high resolution encoders.

I'm not quite sure how to think of how these all fit together to form "robotics" and whether they are small elements of a larger thing, or large breakthroughs stacked over the course of many years (where they might appear small at that zoomed out level).

I think that if we take a snapshot in a specific time (e.g. 5 years) in robotics, there will often be one or very few large bottlenecks that are holding it back. Right now it is mostly ML/vision and batteries. 10-15 years ago, maybe it was the CPU real time processing latency or the motor power density. A bit earlier it might be gearbox. These things were fairly major bottlenecks until they got good enough that it switches to a minor revision/iteration regime (nowadays there's not much left to improve on gearboxes e.g., except for maybe in very specific use cases)

[-]Matt Vincent1mo20

typically don't interact non-trivially

Or, as Orwell would prefer, "typically interact trivially".

[-]Martin Randall2mo340

The fourth friend, Becky the Backward Chainer, started from their hotel in LA and...

Well, no. She started at home with a telephone directory. A directory seems intelligent but is actually a giant look-up table. It gave her the hotel phone number. Ring ring.

Heidi the Hotel Receptionist: Hello?

Becky: Hi, we have a reservation for tomorrow evening. I'm back-chaining here, what's the last thing we'll do before arriving?

Heidi: It's traditional to walk in through the doors to reception. You could park on the street, or we have a parking lot that's a dollar a night. That sounds cheap but it's not because we're in the past. Would you like to reserve a spot?

Becky: Yes please, we're in the past so our car's easy to break into. What's the best way to drive to the parking lot, and what's the best way to get from the parking lot to reception?

Heidi: We have signs from the parking lot to reception. Which way are you driving in from?

Becky: Ah, I don't know, Alice is taking care of that, and she's stepped out to get more string.

Heidi: Oh, sure, can't plan a car trip without string. In the future we'll have pet nanotech spiders that can make string for us, road trips will never be the same. Anyway, you'll probably be coming in via Highway 101, or maybe via the I-5, so give us a buzz when you know.

Becky: Sorry, I'm actually calling from an analogy, so we're planning everything in parallel.

Heidi: No worries, I get stuck in thought experiments all the time. Yesterday my friend opened a box and got a million dollars, no joke. Look, get something to take notes and I'll give you directions from the three main ways you could be coming in.

Becky: Ack! Hang on while I...

Gerald the General Helper: Here's a pen, Becky.

Trevor the Clever: Get off the phone! I need to call a gas station!

Susan the Subproblem Solver: Alice, I found some string and.... Hey, where's Alice?

[-]Ruby2mo246

This doesn't seem right. Suppose there are two main candidates for how to get there, I-5 and J-6 (but who knows, maybe we'll be surprised by a K-7) and I don't know which Alice will choose. Suppose I know there's already a Very General Helper and Kinda Decent Generalizer, then I might say "I assign 65% chance that Alice is going to choose the I-5 and will try to contribute having conditioned on that". This seems like a reasonable thing to do. It might be for naught, but I'd guess in many case the EV of something definitely helpful if we go down Route A is better than the EV of finding something that's helpful no matter the choice.

One should definitely track the major route they're betting on and make updates and maybe switch, but seems okay to say your plan is conditioning on some bigger plan.

[-]johnswentworth2mo1511

Yup, if you actually have enough knowledge to narrow it down to e.g. a 65% chance of one particular major route, then you're good. The challenging case is when you have no idea what the options even are for the major route, and the possibility space is huge.

[-]Ariel2mo215

Besides reiterating Ryan Greenblat's objection to the assumption of a single bottleneck problem, I would also like to add that there is apriori value in having many weakly generalizable solutions even if only few will have posteriori value.

Designing only best-worst-case subproblem solutions while waiting for Alice would be like restricting strategies in game to ones agnostic to the opponent's moves, or only founding startups that solve a modal person's problem. That's not to say that generalizability isn't a good quality, but I think the claim in the article goes a little too far.

There's one common reason I sometimes undervalue weakly-generalizeable solutions (it's not in response to any claim in the article, but I hope it is relevant still): it sucks to be the individual researcher whose work turns out as irrelevant. I think that both in a utilitarian sense and as a personal way to cope with life, it's better to adopt an apriori mindset of meaning and value in one's work, but we're not naturally equipped with it.

[-]Noosphere892mo93

I would go further, and say that one of the core problem-solving strategies that are done to attack hard problems, especially of the NP-complete/NP-hard problems is to ask for less robustly generalizable solutions, and being more willing to depend on assumptions that might work, but also might not, because trying to find a robustly generalizable solution is too hard.

Indeed, one way of problem relaxation is to assume more structure about the problem you are studying, such that you can get instances that can actually be solved in a reasonable amount of time.

I think there's something to the "focus on bottlenecks" point, but also I think that trying to be too general instead of specializing and admitting your work might be useless is a key reason why people fail to progress.

[-]Elliot Callender2mo*30

I think general solutions are especially important for fields with big solution spaces / few researchers, like alignment. ~~If you were optimizing for, say, curing cancer, it might be different (I think both the paradigm-and subproblem-spaces are smaller there).~~

From my reading of John Wentworth's Framing Practicum sequence, implicit in his (and my) model is that solution spaces for these sorts of problems are apriori enormous. We (you and I) might also disagree on what apriori feasibility would be "weakly" vs "strongly" generalizable; I think my transition is around 15-30%.

[-]Ariel2mo40

I see what you mean with regards to the number of researchers. I do wonder a lot about the amount of waste from multiple researchers unknowingly coming up with the same research (a different problem to what you pointed out) and the uncoordinated solution to that is to work on niche problems and ideas (which coincidentally seem less likely to individually generalize).

Could you share your intuition for why the solution space in AI alignment research is large, or larger than in cancer? I don't have an intuition about the solution space in alignment v.s. a "typical" field, but I strongly think cancer research has a huge space and can't think of anything more difficult within biology. Intuition: you can think of fighting cancer as a two player game, with each individual organism being an instance and the within-organism evolutionary processes leading to cancer being the other player. In most problems in biology you can think about the genome of the organisms as defining rule set for the game, but here the genome isn't held constant.

w.r.t. to the threshold to strong generalizability, I don't have a working model of this to disagree with. Putting confidence/probability values on relatively abstract things is something I'm not used to (and I understand is encouraged here), so I'd appreciate if you could share a little more insight about how to

Define the baseline distribution generalizability is defined on.
Give a little intuition about why a threshold is meaningful, rather than a linear "more general is better".

I'm sorry if that's too much to ask for or ignorant of something you've laid out before. I have no intuition about #2, but for #1 I suspect that you have a model of AI alignment or an abstract field as having a single/few central problems at a time, whereas my intuition is that they are mostly composed of many problems, with "centrality" only being relevant as a storytelling device or a good way to make sense of past progress in retrospect (so that generalizability is more the chance that one work will be useful for another, rather than be useful following a solution to the central problem) . More concretely, aging may be a general factor to many diseases, but research into many of the things aging relates to is composed of solving many small problems that do not directly relate to aging, and defining solving aging as a bottleneck problem and judging generalizability with respect to it doesn't seem useful.

[-]Elliot Callender2mo20

I strongly think cancer research has a huge space and can't think of anything more difficult within biology.

I was being careless / unreflective about the size of the cancer solution space, by splitting the solution spaces of alignment and cancer differently; nor do I know enough about cancer to make such claims. I split the space into immunotherapies, things which target epigenetics / stem cells, and "other", where in retrospect the latter probably has the optimal solution. This groups many small problems with possibly weakly-general solutions into a "bottleneck", as you mentioned:

aging may be a general factor to many diseases, but research into many of the things aging relates to is composed of solving many small problems that do not directly relate to aging, and defining solving aging as a bottleneck problem and judging generalizability with respect to it doesn't seem useful.

Later:

Define the baseline distribution generalizability is defined on.

For a given problem, generalizability is how likely a given sub-solution is to be part of the final solution, assuming you solve the whole problem. You might choose to model expected utility, if that differs between full solutions; I chose not to here because I natively separate generality from power.

Give a little intuition about why a threshold is meaningful, rather than a linear "more general is better".

I agree that "more general is better" with a linear or slightly superlinear (because you can make plans which rely heavier on solution) association with success probability. We were already making different value statements about "weakly" vs "strongly" general, where putting concrete probabilities / ranges might reveal us to agree w.r.t the baseline distribution of generalizability and disagree only on semantics.

I.e. thresholds are only useful for communication.

Perhaps a better way to frame this is in ratios of tractability (how hard to identify and solve) and usefulness (conditional on the solution working) between solutions with different levels generalizability. E.g. suppose some solution is 5x less general than $g$ . Then you expect, for the types of problems and solutions humans encounter, that $w$ will be more than 5x as tractable * useful as $g$ .

I disagree in expectation, meaning for now I target most of my search at general solutions.

My model of the central AIS problems:

How to make some AI do what we want? (under immense functionally adversarial pressures)
1. Why does the AI do things? (Abstractions / context-dependent heuristics; how do agents split reality given assumptions about training / architecture)
2. How do we change those things-which-cause-AI-behavior?
How do we use behavior specification to maximize our lightcone?
1. How to actually get technical alignment into a capable AI? (AI labs / governments)
2. What do we want the AI to do? ("Long reflection" / CEV / other)

I'd be extremely interested to hear anyone's take on my model of the central problems.

[-]Ariel2mo*90

Thank you, that was very informative.

I don't find the "probability of inclusion in final solution" model very useful, compared to "probability of use in future work" (similarly for their expected value versions) because

I doubt that central problems are a good model for science or problem solving in general (or even in the navigation analogy).
I see value in impermanent improvements (e.g. current status of HIV/AIDS in rich countries) and in future-discounting our value estimations.
Even if a good description of a field as a central problem and satalite problems exists, we are unlikely to correctly estimate it apriori, or estimate the relevance of a solution to it. In comparison, predicting how useful a solution is to "nearby" work is easier (with the caveat that islands or cliques of only internaly-useful problems and solutions can arise, and do in practice).

Given my model, I think 20% generalizability is worth a person's time. Given yours, I'd say 1% is enough.

[-]Elliot Callender1mo10

How much would you say (3) supports (1) on your model? I'm still pretty new to AIS and am updating from your model.

I agree that marginal improvements are good for fields like medicine, and perhaps so too AIS. E.g. I can imagine self-other overlap scaling to near-ASI, though I'm doubtful about stability under reflection. I'll put 35% we find a semi-robust solution sufficient to not kill everyone.

Given my model, I think 20% generalizability is worth a person's time. Given yours, I'd say 1% is enough.

I think that the distribution of success probability of typical optimal-from-our-perspective solutions is very wide for both of the ways we describe generalizability; within that, we should weight generalizability heavier than my understanding of your model does.

Earlier:

Designing only best-worst-case subproblem solutions while waiting for Alice would be like restricting strategies in game to ones agnostic to the opponent's moves

Is this saying people should coordinate in case valuable solutions aren't in the apriori generalizable space?

[-]Elizabeth2mo123

Reasoning through a new example:

There's no google maps and no internet to help with finding a hotel. You haven't chosen a destination city yet.

You could work out how to choose hotels and facilitate the group identifying the kind of hotel it wants. They're both robustly useful.

You could start picking out hotels in cities at random. Somehow my intuition is that doing this when you don't know the city is still marginally useful (you might choose that city. Obviously more useful the smaller the set of possible cities), but nonzero useful.

OTOH, one of the best ways to build hotel identifying skills is to identify a hotel, even if you don't use it. A few practice runs choosing hotels in random cities probably does help you make a new reservation in a different city.

My shoulder John says "dry running hotels is a fine thing to do as long as you're doing it as a part of a plan to get good at a generalizable skill". I agree that's ideal, but not everyone has that skill, and one of the ways to get it is to gradient ascend on gradient ascending. I worry that rhetoric like this, and related stuff I see in EA and rationality encouraging people to do the most important thing, ends up paralyzing people when what they need is to do anything so they can start iterating on it.

[-]CronoDAS2mo20

Hmmm. Taking this literally, if I didn't know where I was going, one thing I might do is look up hotel chains and find out which ones suit my needs with respect to price level and features and which don't, so when I know what city I want to travel to, I can then find out if my top choices of hotel chain have a hotel in a convenient location there.

Meta-strategy: try to find things that are both relevant to what you want and mostly independent of the things you don't know about?

[-]NickH1mo110

In research you don't usually know your precise destination. Maybe LA but definitely not the hotel.
research, in general, is about mapping all of California, not just the quickest route between two points and all the friends helped with that.
You say "Alice tackled the central bottleneck" but you don't say what that was, only her "solution". Alice is only key here with the benefit of hindsight. If the I5 didn't exist or was closed for some reason then one of her friends solutions might have been better.

[-]Kaj_Sotala2mo106

If you do not choose robustly generalizable subproblems and find robustly generalizable solutions to them, then most likely, your contribution will not be small; it will be completely worthless.

Though it also feels worth noting that while individually unsatisfying, it's not necessarily collectively wrong for a lot of people to work on subproblems that will turn out to be completely worthless. If one of them turns out to unexpectedly solve the main bottleneck after all, or if several of them do end up making small progress that lets someone else solve the main bottleneck, all of the "wasted" work may in fact have bought us the useful bits that you couldn't have identified in advance.

Often when I've had a hypothesis about something that interests me, I've been happy that there has been *so much* scientific research done on various topics, many of them seemingly insignificant. While most of it is of little interest to me, the fact that there's so much of it means that there's often some prior work on topics that do interest me. And vice versa - much of the work that I find uninteresting, will probably be a useful puzzle piece in someone else's research. (Even if a lot of it is also genuinely useless for everyone, but that's the price we pay for getting some of the more useful bits.)

[-]johnswentworth2mo74

That sort of reasoning makes sense insofar as it's hard to predict which small pieces will be useful. And while that is hard to some extent, it is not full we-just-have-no-idea-so-use-a-maxent-prior hard. There is plenty of work (including lots of research which people sink their lives into today) which will predictably-in-advance be worthless. And robust generalizability is the main test I know of for that purpose.

Applying this to your own argument:

Often when I've had a hypothesis about something that interests me, I've been happy that there has been *so much* scientific research done on various topics, many of them seemingly insignificant. While most of it is of little interest to me, the fact that there's so much of it means that there's often some prior work on topics that do interest me.

It will predictably and systematically be the robustly generalizable things which are relevant to other people in unexpected ways.

[-]johnswentworth2mo1410

Now to get a little more harsh...

Without necessarily accusing Kaj specifically, this general type of argument feels motivated to me. It feels like willful ignorance, like sticking one's head in the sand and ignoring the available information, because one wants to believe that All Research is Valuable or that one's own research is valuable or some such, rather than facing the harsh truth that much research (possibly one's own) is predictably-in-advance worthless.

[-]Kaj_Sotala2mo186

It is probably often motivated in that way, though interestingly something I had in mind while writing my comment was something like an opposite bias (likewise not accusing you specifically of it). In that in rationalist/EA circles it sometimes feels like everyone (myself included) wants to do the meta-research, the synthesizing across disciplines, the solving of the key bottlenecks etc. and there's a relative lack of interest in the object-level research, the stamp collecting, the putting things in place that's a prerequisite for understanding and solving the key bottlenecks. In a way that puts the meta stuff as the highest good while glossing over the fact that the meta stuff only works if someone else has done the basic research it builds on first.

Now your post wasn't framed in terms of meta-research vs. object-level research nor of theory-building vs. stamp-collecting or anything like that, so this criticism doesn't apply to your post as a whole. But I think the algorithm of "try to ensure that your research is valuable and not useless" that I was responding to, while by itself sensible, can easily be (mis?)applied in a way that causes one to gravitate toward more meta/theory stuff. (Especially if people do the often-tempting move of using the prestige of a discovery as a proxy for its usefulness.) This can then, I think, increase the probability that the individual gets to claim credit for a shiny-looking discovery while reducing the probability that they'll do something more generally beneficial.

Toy model: suppose that each empirical result has some probability of being useful. For every U useful empirical results, there are T theoretical discoveries to be made that generalize across those empirical results. Suppose that useful empirical results give you a little prestige while theoretical discoveries give you a lot of prestige, and each scientist can work on either empiricism or theory. Given enough empirical findings, each theorist has some probability of making a theoretical discovery over time.

Then past a certain point, becoming a theorist will not make it significantly more likely that science overall advances (as the number of theoretical discoveries to be made is bounded by the number of empirical findings and some other theorist would have been likely to make the same discovery), but it does increase that theorist's personal odds of getting a lot of prestige. At the same time, society might be better off if more people were working on empirical findings, as that allowed more theoretical discoveries to be made.

Of course this is a pretty general and abstract argument and it only applies if the balance of theorists vs. empiricists is in fact excessively tilted toward the theorists. I don't know whether that's true, I could easily imagine that the opposite was. (And again it's not directly related to most of what you were saying in your post, though there's a possible analogous argument to be made about whether there was any predictably useful work left to be done in the first place once Alice, The Very General Helper, and The One Who Actually Thought This Through A Bit were already working on their respective approaches.)

[-]Dzoldzaya1mo10

There's a world of difference between "let's just continue doing this research project on something obscure with no theory of impact because penicillin" and "this is more likely than not to become irrelevant in 18 months time, but if it works, it will be a game-changer".

Robustness and generalizability are subcomponents of the expected value of your work/research. If you think that these are neglected, and that your field is too focused on the "impact" components of EV, i.e. there are too many moon shots, please clarify that, but your analogy fails to make this argument.

As it is, I suspect that optimizing for robust generalizability is a sure-fire way of ensuring that most people become "very general helpers", which seems like a very harmful thing to promote.

[-]CronoDAS2mo30

<irony>Robustly generalizible like noticing that bacteria aren't growing next to a certain kind of mold that contaminated your petri dish or that photographic film is getting fogged when there's no obvious source of light?</irony>

[-]plex2mo104

Seems accurate, though I think Thinking This Through A Bit involved the part of backchaining where you look at approximately where on the map the destination is, and that's what some pro-backchain people are trying to point at. In the non-metaphor, the destination is not well specified by people in most categories, and might be like 50 ft in the air so you need a way to go up or something.

And maybe if you are assisting someone else who has well grounded models, you might be able to subproblem solve within their plan and do good, but you're betting your impact on their direction. Much better to have your own compass or at least a gears model of theirs so you can check and orient reliably.

PS: I brought snacks!

[-]Raemon1mo7-2

Curated. I found this a clearer explanation of "how to think about bottlenecks, and things that are not-especially-bottlenecks-but-might-be-helpful" than I previously had.

Previously, I had thought about major bottlenecks, and I had some vague sense of "well, there definitely seems like there should be more ways to be helpful than just tackling central bottlenecks, but a lot of ways to do that misguidedly." But I didn't have any particular models for thinking about it, and I don't think I could have explained it very well.

I think there are better ways of doing forward-chaining and backward-chaining than listed here (but which roughly correspond to "the one who thought about it a bit," but with a bit more technique for getting traction).

I do think the question of "to what degree is your field shaped like 'there's a central bottleneck that is to a first approximation the only thing that matters here'?" is an important question that hasn't really been argued for here. (I can't recall offhand if John has previously written a post exactly doing that in those terms, although the Gears Which Turn the World sequence is at least looking at the same problemspace)

[-]PhilGoetz1mo60

I don't see how to map this onto scientific progress. It almost seems to be a rule that most fields spend most of their time divided for years between two competing theories or approaches, maybe because scientists always want a competing theory, and because competing theories take a long time to resolve. Famous examples include

geocentric vs heliocentric astronomy
phlogiston vs oxygen
wave vs particle
symbolic AI vs neural networks
probabilistic vs T/F grammar
prescriptive vs descriptive grammar
universal vs particular grammar
transformer vs LSTM

Instead of a central bottleneck, you have central questions, each with more than one possible answer. Work consists of working out the details of different experiments to see if they support or refute the possible answers. Sometimes the two possible answers turn out to be the same (wave vs matrix mechanics), sometimes the supposedly hard opposition between them dissolves (behaviorism vs representationalism), sometimes both remain useful (wave vs particle, transformer vs LSTM), sometimes one is really right and the other is just wrong (phlogiston vs oxygen).

And the whole thing has a fractal structure; each central question produces subsidiary questions to answer when working with one hypothesized answer to the central question.

It's more like trying to get from SF to LA when your map has roads but not intersections, and you have to drive down each road to see whether it connects to the next one or not. Lots of people work on testing different parts of the map at the same time, and no one's work is wasted, although the people who discover the roads that connect get nearly all the credit, and the ones who discover that certain roads don't connect get very little.

[-]Shmi1mo50

Looks like the hardest part in this model is how to " choose robustly generalizable subproblems and find robustly generalizable solutions to them", right?

How does one do that in any systematic way? What are the examples from your own research experience where this worked well, or at all?

[-]Raemon1mo51

I think the Gears Which Turn The World sequence, and Specializing in Problems We Don't Understand, and some other scattered John posts I don't remember as well, are a decent chunk of an answer.

[-]TsviBT2mo*50

When they're nearing the hotel, Alice gets the car's attention. And she's like, "Listen guys, I have been lying to you. My real name is Mindy. Mindy the Middlechainer.".

[-]eggsyntax1d40

(Much belated comment, but:)

There are two roles that don't show up in your trip planning example but which I think are important and valuable in AI safety: the Time Buyer and the Trip Canceler.

It's not at all clear how long it will take Alice to solve the central bottleneck (or for that matter if she'll be able to solve it at all). The Time Buyer tries to find solutions that may not generalize to the hardest version of the problem but will hold off disaster long enough for the central bottleneck to be solved.

The Trip Canceler tries to convince everyone to cancel the trip so that the fully general solution isn't needed at all (or at least to delay it long enough for Alice to have plenty of time to work.

They may seem less like the hero of the story, but they're both playing vital roles.

[-]CronoDAS2mo42

Elaborating on The Very General Helper Strategy: the first thing you do when planning a route by hand is find some reasonably up-to-date maps.

One thing that almost always tends to robustly generalize is improving the tools that people use to gather information and make measurements. And this also tends to snowball in unexpected ways - would anyone have guessed beforehand that the most important invention in the history of medicine would turn out to be a better magnifying glass? (And tools can include mathematical techniques, too - being able to run statistical analysis on a computer lets you find a lot of patterns you wouldn't be able to find if it was 1920 and you had to do it all by hand.)

With regards to AI, that might mean interpretability research?

[-]David James1mo30

I find this article confusing. So I find myself returning to fundamentals of computer science algorithms: to greedy algorithms and under what conditions they are optimal. Would anyone care to build a bridge from this terminology to what the author is trying to convey?

[-]Garrett Baker1mo40

I think the connection would come from the concept of a Lagrangian dual problem in optimization. See also John's Mazes and Duality.

Moderation Log