This post was written in response to Evan Hubinger’s shortform prompt below and benefited from discussions with him. Thanks to Justis Mills for feedback on this post.
If we see precursors to deception (e.g. non-myopia, self-awareness, etc.) but suspiciously don’t see deception itself, that’s evidence for deception.
Setup
Suppose an AI lab tries to look for the capabilities that enable deceptive alignment. This definitely seems like a good thing for them to do. Say they search for evidence of models optimizing past the current training epoch, for manipulation during human feedback sessions, for situational awareness, and so on. Suppose that when all is said and done they see the following:
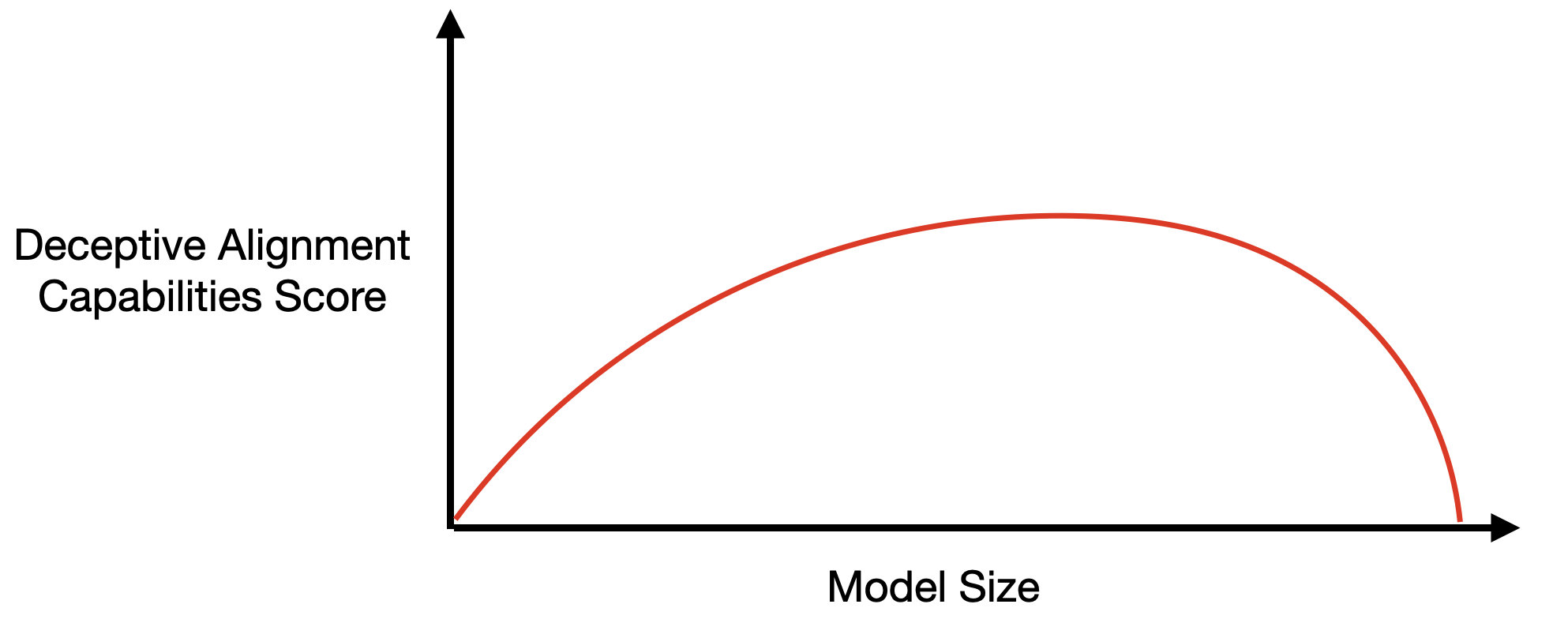 There are at least two ways to interpret this:
There are at least two ways to interpret this:
- “Phew, bigger models are less likely to be deceptively aligned than small ones. Scale away!”
- “Bigger models are more capable at hiding their deceptive alignment. Run away!”
These are very different interpretations, with very different recommendations, so we’d really like to know which to put more credence in.
Priors
Going in, I think we should have a prior that capabilities getting worse with increasing scale is unlikely. We know of specific examples thanks to the inverse scaling prize, but these are rare exceptions to the general rule of increasing capabilities with increasing scale. As a result, a decreasing deceptive capabilities score should be suspicious.
The flip side is that it’s conceivable that some alignment problems get easier with scale. Larger language models understand more of what we say and value (e.g. Figure 8 of Bai+22), and so in some sense outer-aligning them may be easier than outer-aligning smaller models. It’s not inconceivable that the same happens for inner alignment, though I wouldn’t want to rely on this happening.
Tests
We don’t have to rely on priors alone. Here are a few ways we might distinguish between interpretations:
- Use transparency tools and figure out what the model is doing.
- Impair bigger models (e.g. with dropout or random or adversarial perturbations) and see if they get better at some deceptive capabilities. Impairing models shouldn’t improve capabilities, so this would be good evidence that the bigger models are capable of deception but choosing to hide that capability.
This experiment is a little tricky to implement, but the core idea is to hope that interventions impair something critical in the model's ability to execute on deception but don't impair all of the deceptive capabilities.
Even if the largest models can continue hiding their capabilities despite the impairment, models that are just barely able to hide their capabilities may fail to do so once impaired, which should increase the model size where deceptive capabilities peak. - Study the models on a very different data distribution. Models that are hiding relevant capabilities may believe they’ve been deployed and reveal their real goals.
Once more, while the largest models may not be fooled by this, models just on the cusp of deceptive alignment are more likely to be tricked and so deceptive alignment may manifest as a shift in the peak of deceptive capabilities towards larger models. - Study which specific capabilities get worse with scale. It’s hard to understand how some capabilities could get worse with scale (e.g. situational awareness, planning ability, etc.) so if those are getting worse that’s really worrying, whereas it’s less obvious if e.g. models should/shouldn’t get more epoch-level myopic with scale.
Scaling Helps
Having access to models of many different sizes is helpful here: we can experiment with small models that are bad at deceptive capabilities, use those results as a baseline, and then try to understand what happens in larger models.
If deceptive alignment occurs, there may well be models of intermediate scale which lie “on the edge” of being capable of deceptive alignment, or which are only weakly capable of it. Those are the ones that we’ll learn the most from and that experiments are most likely to catch.
Challenge: deceptive models know this
A big challenge to the empirical approaches above (other than interpretability) is that deceptive models may realize that we’re likely to do this sort of test. If a deceptive model realizes that we won’t deploy models that show peaked deceptive capabilities, it can choose a policy where e.g. deceptive capabilities level off rather than falling.
The same reasoning follows for any behavior we come to expect. The model may well be able to do the same reasoning, realize what we expect it to do, and do something else instead.
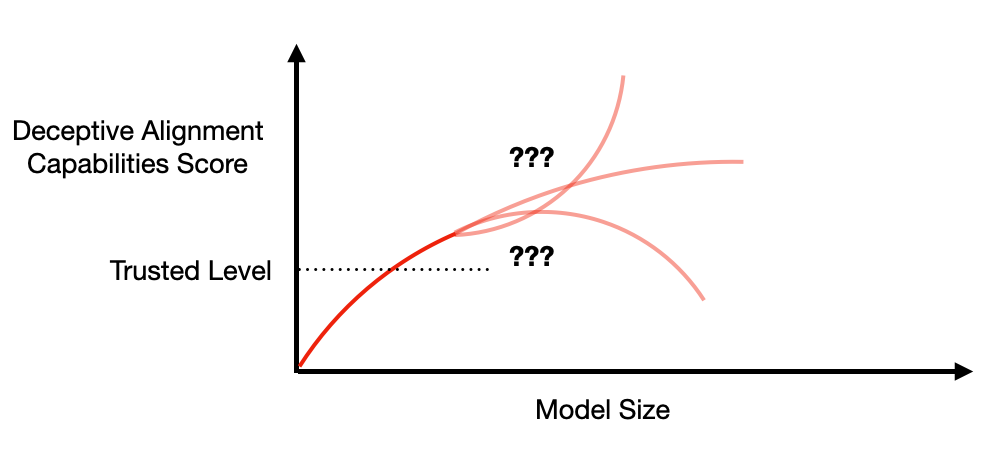 This suggests a strategy where we decide on a level of deceptive capabilities that’s low enough that we trust models not to be deceptively aligned. If we see deceptive capabilities increasing up to this “trusted level” we just don’t deploy those models, because beyond the trusted level we’re engaging with a potentially deceptive adversary rather than an unaware experimental subject.
This suggests a strategy where we decide on a level of deceptive capabilities that’s low enough that we trust models not to be deceptively aligned. If we see deceptive capabilities increasing up to this “trusted level” we just don’t deploy those models, because beyond the trusted level we’re engaging with a potentially deceptive adversary rather than an unaware experimental subject.
Of course determining the trusted level is hard, as is the coordination needed to get labs to commit to not deploying models above that level. But it seems worth trying, and could naturally be a part of a program to monitor for deceptive alignment.
Summary
I think we should be quite suspicious if we see that larger models are worse at the capabilities needed for deceptive alignment. The natural explanation there is that larger models are deceptively aligned and are hiding their capabilities.
At the same time, there are lots of experiments we can do to understand if that’s what’s going on, and the fact that capabilities are strongly related to model scale means that we can use models that are definitely incapable of deceptive alignment as a baseline. If we see no increase in deceptive capabilities as those models scale up, that feels like good evidence against deceptive alignment, because at some scale the model should have been just-barely-incapable of deceptive alignment and so revealed its increased deceptive capabilities.
Unfortunately, what seems more likely is that deceptive capabilities will increase with model scale, just because capabilities generally increase with scale. Above some threshold level of deceptive capabilities we should stop trusting the results of behavioral experiments no matter what they show, because anything they show could be a result of deceptive alignment. So determining what level of deceptive capabilities we ought to trust seems important as a way of enabling an empirically-oriented posture of “trust, but verify”.
Toy example. Their are 3 possible AI's. For simplicity assume a prior where each has a 1/3rd chance of existing. (1) The one that is honest, (2) the one that will try and deceive you but be detected, and (3) the one that will deceive, but do so well enough to not be detected.
We either detect deception or we do not (I agree this is binary). In the event we detect deception we can rule out options (1) and (3), and thus update to believing we have AI number (2) (with probability 1). In the event we do not detect deception we rule out option (2), and thus (if the evidence was perfect) we would update to a 50/50 distribution over options (1) and (3) - so that the probability we assign to option (3) has increased from 1/3 to 1/2.
State: probabilities over (1), (2), (3)
Before test: 1/3, 1/3, 1/3
If test reveals deception: 0, 1, 0
If no deception detected: 1/2, 0, 1/2
I agree that the opening sentence that localdiety quotes above, taken alone, is highly suspect. It does fall foul of the rule, as it does not draw a distinction between options (2) and (3) - both are labelled "deceptive"*. However, in its wider context the article is, I think, making a point like the one outlined in my toy example. The fact that seeing no deception narrows us down to options (1) and (3) is the context for the discussion about priors and scaling-laws and so on in the rest of the original post. (See the two options under "There are at least two ways to interpret this:" in the main post - those two ways are options (1) and (3)).
* clumping the two "deceptive" ones together the conservation holds fine. The probability of having either (2) or (3) was initially 2/3. After the test it is either 1 or 1/2 depending on the outcome of the test. The test has a 1/3 chance of gaining us a 1/3rd certainty of deception, and it has a 2/3 chance of loosing us a 1/6 certainty of deception. So the conservation works out, if you look at it in the binary way. But I think the context for the post is that what we really care about is whether we have option (3) or not, and the lack of deception detected (in the simplistic view) increases the odds of (3).