This is a relatively clean subproblem that we came upon a few months ago while thinking about gradient hacking. We're throwing it out to the world to see if anyone can make progress.
Problem: Construct a gradient hacker (definition below), or prove that one cannot exist under the given conditions.
Setup: Let be the network inputs, , be the network trainable parameters, be the network outputs, and be the network architecture. must be a feedforward neural network that reads in its own weights as input. Weight sharing is allowed (vertical or horizontal), and some weight sharing is necessary in order to take all w weights as input.
Suppose that we train this network on a dataset , with MSE loss , assuming gradient flows: . Given an initial point , the training dynamics are therefore:
Definition: A tuple is a gradient hacker if the following conditions hold:
- is not a global optimum: such that
- such that :
- the network’s training converges to , i.e., .
- There is internal structure of that computes the gradient; i.e., there is some subset of the activations whose mean over every datapoint in D is . [1]
This captures my intuition that a gradient hacker knows where it wants to go (in this case "get to "), and then it should decide what it outputs in order to make the gradient true.
Some more ambitious problems (if gradient hackers exist):
- Characterize the set of all gradient hackers.
- Show that they all must satisfy some property.
- Construct gradient hackers for arbitrarily large , , , and neural net depth.
- Variations on the problem: a subset of the activations equals for every input, or the subset of activations correspond to the gradient on that input.
- ^
This is a bit strict, but we didn't want to list different ways something could be isomorphic to the gradient.
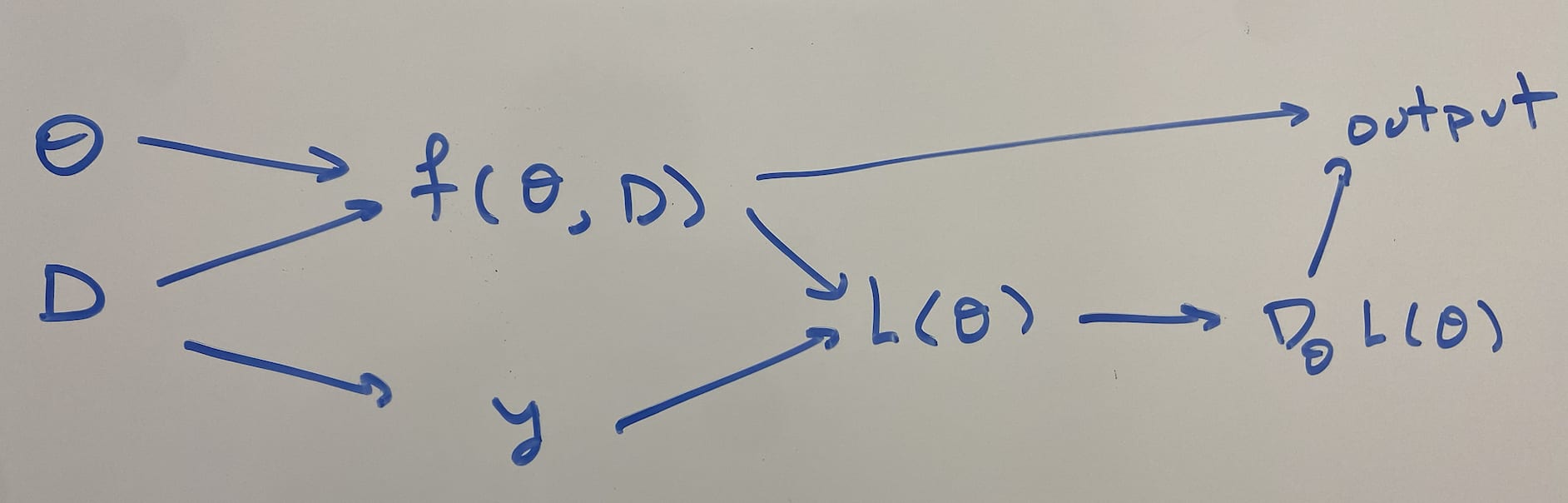
This feels like cheating to me, but I guess I wasn't super precise with 'feedforward neural network'. I meant 'fully connected neural network', so the gradient computation has to be connected by parameters to the outputs. Specifically, I require that you can write the network as
f(x,θ)=σn∘Wn∘…σ1∘W1[x,θ]Twhere the weight matrices are some nice function of θ (where we need a weight sharing function to make the dimensions work out. The weight sharing function takes in ϕ and produces the Wi matrices that are actually used in the forward pass.)
I guess I should be more precise about what 'nice means', to rule out weight sharing functions that always zero out input, but it turns out this is kind of tricky. Let's require the weight sharing function ϕ:Rw→RW to be differentiable and have image that satisfies [−1,1]⊂projnim(ϕ) for any projection. (A weaker condition is if the weight sharing function can only duplicate parameters).