(thanks to Tao Lin and Ryan Greenblatt for pointing this out, and to Arthur Conmy, Jenny Nitishinskaya, Thomas Huck, Neel Nanda, and Lawrence Chan, Ben Toner, and Chris Olah for comments, and many others for useful discussion.)
In “A Mathematical Framework for Transformer Circuits”, Elhage et al write (among similar sentences):
One layer attention-only transformers are an ensemble of bigram and “skip-trigram” (sequences of the form "A… B C") models. The bigram and skip-trigram tables can be accessed directly from the weights, without running the model.
When I first read this, I (and at least some other readers) interpreted this as a mathematical claim–that the attention layer of a one-layer transformer can be mathematically rewritten as a set of skip-trigrams, and that you can understand the models by reading these skip-trigrams off the model weights (and also reading the bigrams off the embed and unembed matrices, as described in the zero-layer transformer section – I agree with this part).
But this mathematical claim is false: One-layer transformers are more expressive than skip-trigrams, so you can’t understand them by transforming them into a set of skip-trigrams. Also, even if a particular one-layer transformer is actually only representing skip-trigrams and bigrams, you still can’t read these off the weights without reference to the data distribution.
The difference between skip-trigrams and one-layer transformers is that when attention heads attend more to one token, they attend less to another token. This means that even single attention heads can implement nonlinear interactions between tokens earlier in the context.
In this post, I’ll demonstrate that one-layer attention-only transformers are more expressive than a set of skip-trigrams, then I’ll tell an intuitive story for why I disagree with Elhage et al’s claim that one-layer attention-only transformers can be put in a form where “all parameters are contextualized and understandable”.
(Elhage et al say in a footnote, “Technically, [the attention pattern] is a function of all possible source tokens from the start to the destination token, as the softmax calculates the score for each via the QK circuit, exponentiates and then normalizes”, but they don’t refer to this fact further.)
An example of a task that is impossible for skip-trigrams but is expressible with one-layer attention-only transformers
Consider the task of predicting the 4th character from the first 3 characters in a case where there are only 4 strings:
ACQT
ADQF
BCQF
BDQT
So the strings are always:
- A or B
- C or D
- Q
- The xor of the first character being A and the second being D, encoded as T or F.
This can’t be solved with skip-trigrams
A skip-trigram (in the sense that Elhage et al are using it) looks at the current token and an earlier token and returns a logit contribution for every possible next token. That is, it’s a pattern of the form
………….X……………………Y -> Z
where you update towards or away from the next token being Z based on the fact that the current token is Y and the token X appeared at a particular location earlier in the context.
(Sometimes the term “skip-trigram” is used to include patterns where Y isn’t immediately before Z. Elhage et al are using this definition because in their context of autoregressive transformers, the kind of trigrams that you can encode involve Y and Z being neighbors.)
In the example I gave here, skip-trigrams can’t help, because the probability that the next token after Q is T is 50% after conditioning on the presence of any single earlier token.
This can be solved by a one-layer, two-headed transformer
We can solve this problem with a one-layer transformer with two heads.
The first attention head has the following behavior, when attending from the token Q (which is the only case we care about):
| Token attending to | Attention score (pre-softmax) | OV behavior |
| A | -10000 | 0 |
| B | 10000 | 0 |
| C | 0 | T |
| D | 0 | F |
| Q | -10000 | 0 |
So it attends almost entirely to B if B is present. If B isn’t present (because the first character was A), it will attend almost entirely to C or D. If it attends to C, it writes T; if it attends to D, it writes F. This head therefore writes the correct answer in cases where the first character was A, and writes nothing otherwise.
(By “OV behavior”, I mean W_U W_{OV} embed. So e.g. I’m saying that if you take the embedding for C, then multiply it by this head’s OV, and then unembed that, you’ll get a vector which is in the direction of the unembed for T.)
The second attention head handles the case where the first character was B:
| Token attending to | Attention score (pre-softmax) | OV behavior |
| A | 10000 | 0 |
| B | -10000 | 0 |
| C | 0 | F |
| D | 0 | T |
| Q | -10000 | 0 |
It’s impossible for an ensemble of skip-trigrams to learn this task, if by “ensemble of skip-trigrams” you mean “a logistic regression where all the features are of the form (token A was at position P and token B is at the current position)”, which is the most reasonable interpretation of how transformers could be considered as a set of skip-trigrams.
Proof sketch: Logistic regressions can only perfectly solve classification problems if there’s a hyperplane separating positive and negative examples. In this case, we’re only able to use the skip-trigrams that tell us whether A or B was at the first position and whether C or D was at the second position. A is only present if B isn’t present, so we only need to have one feature that represents the token at the first position; likewise for C and D. So we’re now considering the logistic regression with two features: “is A at the first position” and “is C at the second position”. It’s impossible to separate the two classes for the usual reason that you can’t learn xor with logistic regression. (Bigrams don’t help in this case because for every input, the current token is Q.) (Thanks to Paul Christiano for help with this proof.) This establishes that one-layer transformers cannot be rewritten as sets of bigrams and skip-trigrams.
In this case, the problem could have been solved if the model could express skip-quadgrams. However, we can construct similar problems that one-layer attention-only transformers can solve that skip-quadgrams can’t. (More generally, because softmax induces a nonlinear infinite-order interaction between all the attention scores, for any fixed n, one-layer attention-only transformers (with an unlimited number of heads and an unlimited vocab size) can express functions that ensembles of skip-n-grams can’t.
(One-layer attention-only transformers can express functions that can’t be expressed by skip-n-grams even if they only have a single attention head. I used multiple attention heads in this example because it allowed me to express xor, which is a particularly clean example of a function that skip-trigrams can’t model at all.)
I think that this transformer is probably pretty easy for SGD to learn–it’s not just a pathological counterexample.
IMO, for reasonable definitions of “understanding”, this falsifies Elhage et al’s claim that you can understand the one-layer transformer from its weights
Elhage et al write:
One layer attention-only transformers are an ensemble of bigram and “skip-trigram” (sequences of the form "A… B C") models. The bigram and skip-trigram tables can be accessed directly from the weights, without running the model.
[...]
By multiplying out the OV and QK circuits, we've succeeded in doing this: the neural network parameters are now simple linear or bilinear functions on tokens. The QK circuit determines which "source" token the present "destination" token attends back to and copies information from, while the OV circuit describes what the resulting effect on the "out" predictions for the next token is. Together, the three tokens involved form a "skip-trigram" of the form [source]... [destination][out], and the "out" is modified.[...]
[...] we do have transformers in a form where all parameters are contextualized and understandable. And despite these subtleties, we can simply read off skip-trigrams from the joint OV and QK matrices.
[...] It seems to us that we now understand this simplified model in the same sense that one might look at the weights of a giant linear regression and understand it, or look at a large database and understand what it means to query it. That is a kind of understanding. There's no longer any algorithmic mystery. The contextualization problem of neural network parameters has been stripped away.
I disagree that they have put their one-layer transformers into a form where all parameters are contextualized and understandable.
To me, what it means to say that a parameter is contextualized and understandable is that you can understand “what role the parameter plays” without learning more about the other parameters or the data distribution. This isn’t true in the example transformer I described above–in both of the heads, you couldn’t really understand why a single attention score had the value it had without looking at the others.
Here’s an intuitive example of how this might come up in a real language model. (I’m not saying that this is actually the best way for the language model to solve the problem I describe, but I am saying that I’m not comfortable assuming this mechanism away without empirical evidence.) Suppose your model has a head that primarily has the responsibility of looking at nouns that appear in news articles and then suggesting related nouns. This head might not do anything on sequences that aren’t news articles (because some of the skip-trigrams it implements are only valid in the context of news articles and not in e.g. Python source files, even though the skip-trigram might appear in the Python source file). It might implement this by attending strongly to Python keywords and then writing nothing. If we just tried to understand the weights of this attention head based on the skip-trigram weights, we’d totally miss the fact that this head turns off its skip-trigrams when in a Python file.
For language models in particular, is the claim that they’re a combination of bigrams and skip-trigrams empirically true?
We’ve established that you can’t always rewrite a one-layer attention-only model as an ensemble of skip-trigrams, but perhaps it’s nevertheless a fairly good approximation for the language models that we train in practice. Some REMIX participants tried to investigate this empirically. I currently don’t have a better way of summarizing their results other than “the model is somewhat but not excellently described as an ensemble of bigrams and skip-trigrams”; perhaps we’ll write something clearer about this at some point.
Is the bigrams-and-skip-trigrams approximation useful for interpretability in practice?
I have no idea. I haven’t seen any persuasive evidence either way.
Does this have any interesting or important implications?
I think the main important point here is this: I’m generally quite skeptical of approaches to interpretability which hope to eventually understand models without reference to their input distribution; it looks to me like the internals of models are intricately related to facts about the data distribution, and we should think about how to use interpretability for alignment by taking this data-distribution-dependence as a given, rather than trying to fight it.

Regarding the more general question of "how much should interpretability make reference to the data distribution?", here are a few thoughts:
Firstly, I think we should obviously make use of the data distribution to some extent (and much of my work has done so!). If you're trying to reverse engineer a regular computer program, it's extremely useful to have traces of that program running. So too with neural networks!
However, the fundamental thing I care about is understanding whether models will be safe off-distribution, so an understanding which is tied to a specific distribution – and especially to a narrow distribution – is less clear in how it advances my core goals. Explanations which hold narrowly but break off distribution are one of my biggest worries for interpretability, and a big part of why I've taken the mechanistic approach rather than picking low-hanging fruit in correlational interpretability. I'm much more worried about explanations only holding on narrow distributions than I am about incomplete global explanations -- this is probably a significant implicit motivator of my research taste. (Caveat: I'm reluctantly okay with certain aspects of understanding being built on the entire training distribution when we have a compelling theoretical argument for why this captures everything and will generalize.)
Let's return to my example of protein binding affinities from my other comment and imagine two different descriptions of the situation:
The global story is a kind of "unbiased account of the mechanism" which requires us to think through more possibilities, but can predict weird out of distribution behavior. On the other hand, the "on distribution story" highlights the aspects of the mechanism which are important in practice, but might fail in weird situations.
But what do we want from the on-distribution analysis?
One easy answer is that we just want to use it to make mechanistic understanding easier. Neural networks are immensely complicated computer programs. It seems to me that even understanding small neural networks is probably comparable to something like "reverse engineer a compiled linux kernel knowing nothing about operating systems". It's very helpful to have examples of it running to kind of bootstrap your analysis.
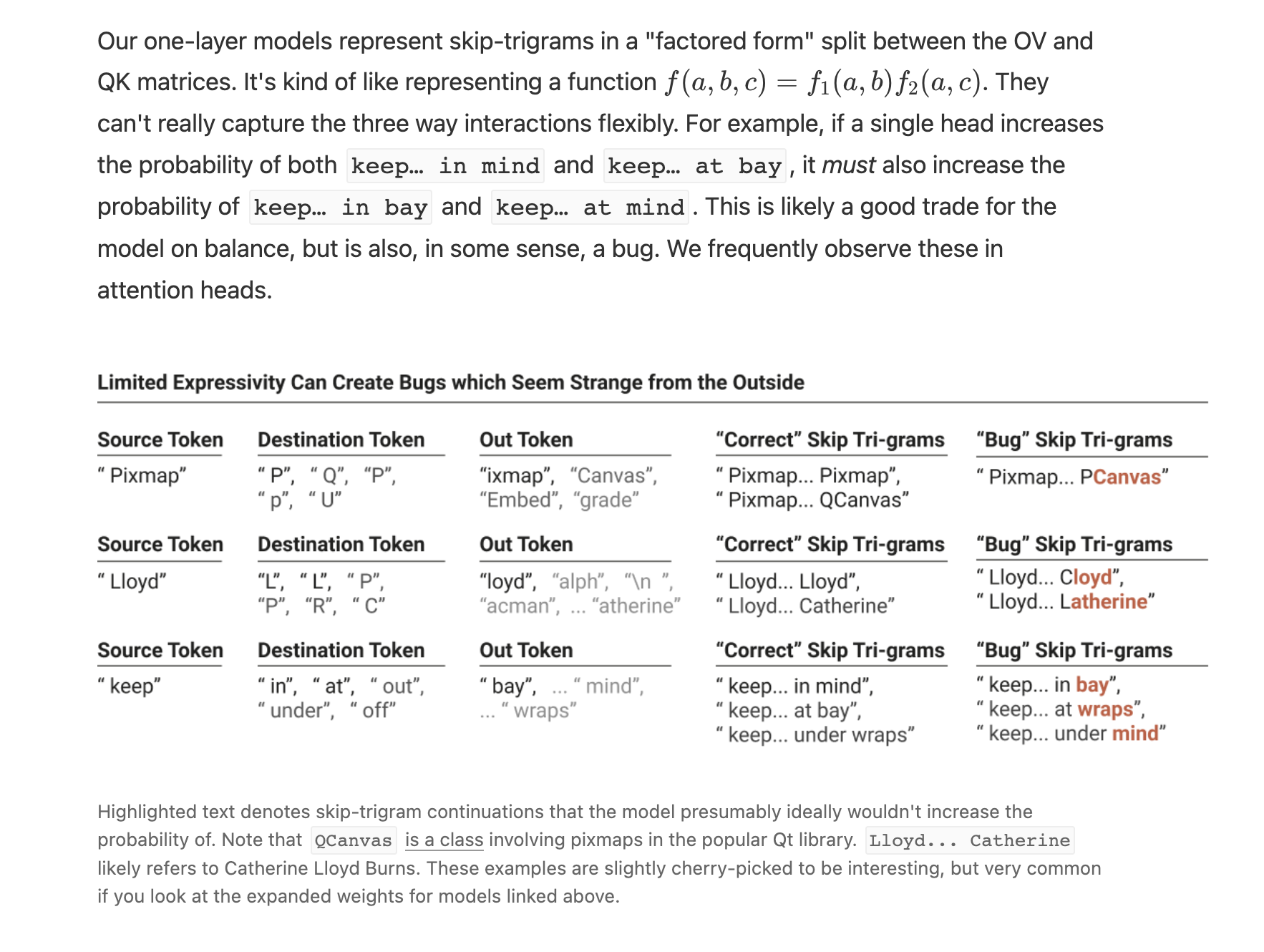
But I think there's something deeper which you're getting at, which I might articulate as distinguishing which aspects of a neural network's mechanistic behavior are "deliberate or useful" and which are "bugs or quirks". For example, in the framework paper we highlight some skip-trigrams which appear to be bugs:
Of course, distinguishing between "correct" skip tri-grams and "bug" skip-trigrams required our judgment based on understanding the domain. In an impartial account of the mechanism, they're all valid skip-trigrams the model implements. It's only with reference to the training distribution or some other external distribution or task that we can think of some as "correct" and others as "bugs".
By more explicitly analyzing on a distribution, one might automate this kind of differentiation. And possibly, one might just ignore these (especially to the extent that other heads or the bigrams can compensate in practice!). This could make a simpler "explanation" at the cost of not generalizing to other distributions.
(In this particular case, I suspect there might actually be a more beautiful, non-distribution specific story to be told in terms of superposition. But that's another topic.)
One interesting thing this suggests is that a "global story" should be able to be "bound" to a distribution to create an in-distribution account. For example, if one has a list of binding affinities for different chemicals, and knows that only a certain subset will be present at the same time, one can produce a summary of which will block each other.
While we're on the topic, it's perhaps useful to more directly describe my concerns about distribution-specific understanding of models, and especially narrow-distribution understanding of the kind a lot of work building Causal Scrubbing seems to be focusing on.
It seems to me that this kind of work is very vulnerable to producing fragile understandings of models which break on a wider distribution due to interpretability illusion type issues.
As one concrete example from my own experience, in the early days of Anthropic I looked into how language models perform arithmetic by only looking at model behavior only on arithmetic expressions. Immediately, lots of interesting patterns popped out and some interesting partial stories began to emerge. However, as soon as I returned to the full training distribution, the story fell apart. All the components I thought did something were doing other things – often primarily doing other things – on the full distribution. Of course, this was a very casual investigation and not anywhere near as rigorous as the causal scrubbing work. But while I'm sure there were ways my understanding on distribution was incomplete, I'm 100x more worried about the fact that it was clearly misleading about the general situation. (My strong suspicion is that there is a very nice story here, but it's deeply intertwined with superposition and we can't understand it without addressing that.)
With that said, I'm very excited for people to be taking different approaches to these problems. My concerns could be misplaced! I definitely think that restricting to a narrow distribution allows one to make a lot of progress on that type of understanding.
Upon further consideration, I think you're probably right that the causal scrubbing results I pointed at aren't actually about the question we were talking about, my mistake.
Seems like probably the optimal strategy. Thanks again for your thoughts here.