In brief: in order to iteratively solve problems of unknown difficulty a good heuristic is to double your efforts every time you attempt it.
Imagine you want to solve a problem, such as getting an organization off the ground or solving a research problem. The problem in question has a difficulty rating , which you cannot know in advance.
You can try to solve the problem as many times as you want, but you need to precommit in advance how much effort you want to put into each attempt - this might be for example because you need to plan in advance how you are going to spend your time.
We are going to assume that there is little transfer of knowledge between attempts, so that each attempt succeeds iff the amount of effort you spend on the problem is greater than its difficulty rating .
The question is - how much effort should you precommit to spend on each attempt so that you solve the problem spending as little effort as possible?
Let's consider one straightforward strategy. We first spend unit of effort, then , then , and so on.
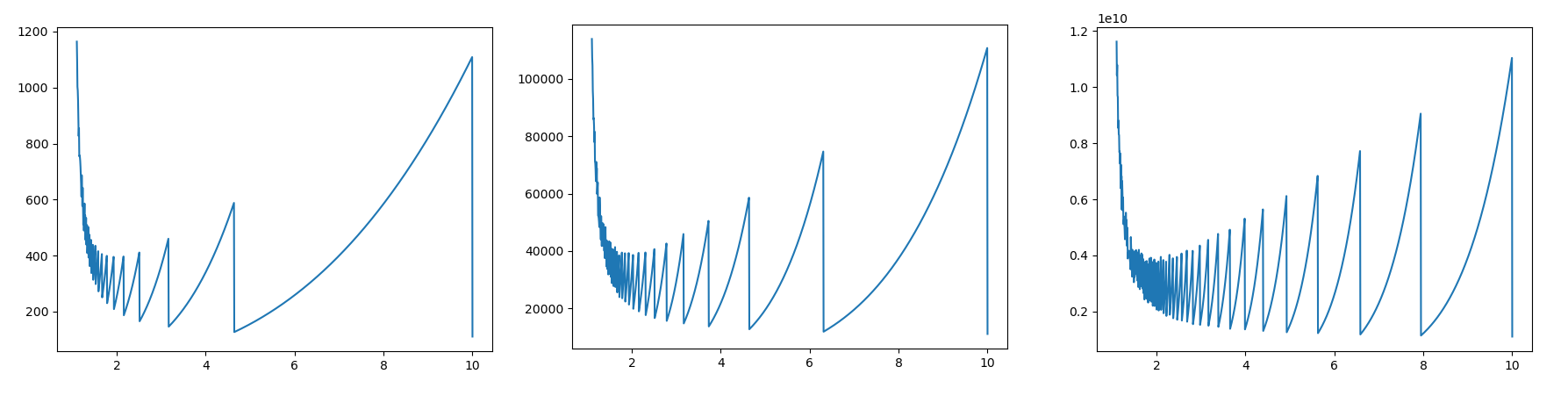
We will have to spend in total . The amount of effort spent scales quadratically with the difficulty of the problem.
Can we do better?
What if we double the effort spent each time?
We will have to spend . Much better than before! The amount of effort spent now scales linearly with the difficulty of the problem.
In complexity terms, you cannot possibly do better - even if we knew in advance the difficulty rating we would need to spend to solve it.
Is doubling the best scaling factor? Maybe if we increase the effort by each time we will spend less total effort.
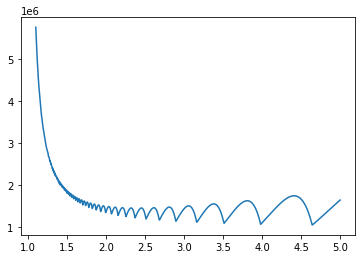
In general, if we scaled our efforts by a factor then we will spend in total . This upper bound is tight at infinitely many points, and its minimum is found for - which asymptotically approaches as grows. Hence seems like a good heuristic scaling factor without additional information on the expected difficulty. But this matters less than the core principle of increasing your effort exponentially.
Real life is not as harsh in our assumptions - usually part of the effort spent carries over between attempts and we have information about the expected difficulty of a problem. But in general I think this is a good heuristic to live by.
Here is an (admittedly shoehorned) example. Let us suppose you are unsure about what to do with your career. You are considering research, but aren't sure yet. If you try out research, you will learn more about that. But you are unsure of how much time you should spend trying out research to gather enough information on whether this is for you.
In this situation, before committing to a three year PhD, you better make sure you spend three months trying out research in an internship. And before that, it seems a wise use of your time to allocate three days to try out research on your own. And you better spend three minutes beforehand thinking about whether you like research.
Thank you to Pablo Villalobos for double-checking the math, creating the graphs and discussing a draft of the post with me.
In gambling, the strategy of repeatedly "doubling down" is called a martingale (google to find previous discussions on LW), and the main criticism is that you may run out of money to bet, before chance finally turns in your favor. Analogously, your formal analysis here doesn't take into account the possibility of running out of time or energy before the desired goal is achieved.
I also have trouble interpreting your concrete example, as an application of the proclaimed strategy. I thought the idea was, you don't know how hard it will be to do something, but you commit to doubling your effort each time you try, however many attempts are necessary. In the example, the goal is apparently to discover whether you should pursue a career in research.
Your proposition is, rather than just jump into a three-year degree, test the waters in a strategy of escalating commitment that starts with as little as three minutes. Maybe you'll find out whether research is the life for you, with only minutes or weeks or months spent, rather than years. OK, that sounds reasonable.
It's as if you're applying the model of escalating commitment from a different angle than usual. Usually it's interpreted as meaning: try, try harder, try harder, try HARDER, try REALLY HARD - and eventually you'll get what you want. Whereas you're saying: instead of beginning with a big commitment, start with the smallest amount of effort possible, that could conceivably help you decide if it's worth it; and then escalate from there, until you know. Probably this already had a name, but I'll call it an "acorn martingale", where "acorn" means that you start as small as possible.
Basically, the gap between your formal argument and your concrete example, is that you never formally say, "be sure to start your martingale with as small a bet/effort as possible". And I think also implicit in your example, is that you know an upper bound on d: doing the full three-year degree should be enough to find out whether you should have done it. You don't mention the possibility that to find out whether you really like research, you might have to follow the degree with six years as a postdoc, twelve years as a professor, zillion years as a posthuman gedankenbot... which is where the classic martingale leads.
But if you do know an upper bound on the task difficulty d, then it should be possible to formally argue that an acorn martingale is optimal, and to view your concrete scenario as an example of this.
In the gambling house, we already know that gambling isn't worth it. The error of the martingale strategy is to think that you can turn lots of non-worthwhile bets into one big worthwhile bet by doubling down (which would be true if you didn't run out of money).
In the world outside the gambling house, we don't do things unless we expect that they're worth the effort. But we might not know what scale of effort is required.
The post didn't offer an analysis of cases where we give up, but I read it with the implicit assumption that we give up when something no... (read more)