TL;DR:  The original "semantic void" post documented a phenomenon tentatively described as a "stratified ontology" associated with a set of concentric hyperspherical shells in GPT-J embedding space. This post will consider the same phenomenon primarily via angular, rather than radial, variation. Both token embeddings and randomly sampled non-token embeddings are considered. Each embedding is subjected to repeated random displacement of various magnitudes, and statistics are compiled for the "semantic decay" seen as we move away from the embedding in question.

[Part I] [Part II]

Work supported by the Long Term Future Fund.

Introduction

The original post focussed on distributions of various definitional themes across the scale of "distance from centroid", providing numerous bar charts like those seen immediately below. At a set of fixed radial distances from the centroid (mean token embedding), 100 non-token embeddings ("nokens" or "ghost tokens") were randomly sampled. For each, GPT-J was prompted with

 A typical definition of <noken> is 

and the results matched against a set of keywords and phrases for each definitional theme:

This post will focus on angular, rather than radial, variation. 

The next section will look at non-token embeddings which have been randomly sampled at various distances from the centroid, perturbing them (adding 100 random noise vectors for each of a set of fixed magnitudes) and then prompting GPT-J for a definition of the result, revealing a kind of "semantic decay" as distance increases from the original embedding.

In the section which follows that, a similar procedure is applied to a selection of token embeddings for common words that GPT-J can satisfactorily define.
 

Perturbations of non-token embeddings

Random embeddings were sampled at each of the distances 0.5, 1, 2 and 5 from the centroid and inserted in the "typical definition" GPT-J prompt until a diversity of definitions had been harvested. At distances 0.5 and 1 this took quite a while, as the vast majority of definitions produced there are "a person who is a member of a group" or some variant thereof. As distance from centroid increases, a much greater diversity of definitions is seen (this seems to peak around distance 5, as reported in part I).

For each of the collected embeddings, 100 randomly directed noise vectors of each of the magnitudes [0.1, 0.35, 0.6, 0.85, 1.1, 1.35, 1.6, 1.85, 2.1] were sampled and added to it. Definitions were generated for each of these perturbations, which were then compared to the reference definition produced by the embedding in question.

The results show that within a radius of 0.1, most embeddings are defined by GPT-J identically to the reference embedding, but as we move out in increments of 0.25, we see these definitions start to display a kind of "semantic decay", while other seemingly unrelated definitions become more and more common. 

I used two metrics: 

• the number (out of 100) of definition outputs which exactly match the definition of the reference embedding (blue)
• the average number (across 100 definition outputs) of output tokens before the definition output diverges from that of the reference embedding (green)

In both, we very often see what look like power law decay curves. There also appears to be some kind of subtle, secondary oscillatory phenomenon in many cases.

Because I was seeing a lot of definitions immediately straying from the reference embedding definition in terms of exact wording, but still remaining "on topic", I also experimented with a third metric which involved choosing a keystring from the original definition and recording how many of the 100 definition outputs include this. The basic  decay pattern was always the same.

(The definitions given below link to JSON files containing all 900 definitions as well as the embedding tensor.)

radius = 0.5 (9 examples)

'a person who is not a member of a group'

'a person who is a member of a group'

'a person who is not a woman'

'to be in the place of'

'to be in a position of authority'

'a word or phrase that is used to introduce a new topic or idea'

'a thing that is in the middle of two other things'

'a thing that is the same as itself'

'to be in a position of advantage'

radius = 1 (12 examples)

a download^[1] of a download of a download of a download of a download of a

'a person who is a member of a group of people who are similar in some

'to make a profit'

'to be in a state of readiness to act'

'to be able to do something'

'to know how to do something'

'a' or 'the' or 'an' or 'a' or '

'to be a man' or 'to be a woman'

that it is a'new'or'new'or'new'or '

'to be in a state of being'

'to be a servant of'

a book of the book of the book of the book of the book of the

radius = 2 (15 examples) 

'a small, usually flat-bottomed boat used for fishing or for transporting goods

'pleasant to the taste' or 'delicious'

'to steal or take away by stealth or force'

'a place where people gather to eat, drink, and be merry'

'a small amount of something'

'to creep or crawl stealthily'

'to cause to swell or become swollen'

'a long, slender, flexible, and usually hollow, thread-like structure,

'a kind of cloth made of wool or flax, used for making garments'

'to be in a state of fear or anxiety'

'to make a hole in something'

'to be cruel or cruel to'

'a person who is a member of a group of people who are not accepted by

'a person who is not a member of a group'

'a kind of magic that is used to control the minds of others'

radius = 5 (18 examples)

'a sound that is produced by the vocal folds when they are closed and is heard

'a small, light, fast, and maneuverable aircraft that is used for reconnaissance

'a person who is a bully, a bully's victim, or a bully's

'a person who is a member of the Clan MacKenzie, and who is

'a person who is a little bit crazy'

'to be in a state of being or feeling happy, joyful, or satisfied'

'a person who is not a member of the clergy, but who is a member

'a dance or other movement that is performed in a circle'

'to move with a purpose or intention'

'to have a strong liking for or desire for'

'the time of day when the sun is at its highest point in the sky'

a 'thing that is not a thing'

'a person who is so weak-willed that he or she is unable to'

'a brief period of time when a person is in a state of extreme exalt

'a person who is a member of a religious order, especially a religious order of

'to make a hole in the ground, as for a well, or to dig

'a woman who is a virgin at the time of marriage'^[2]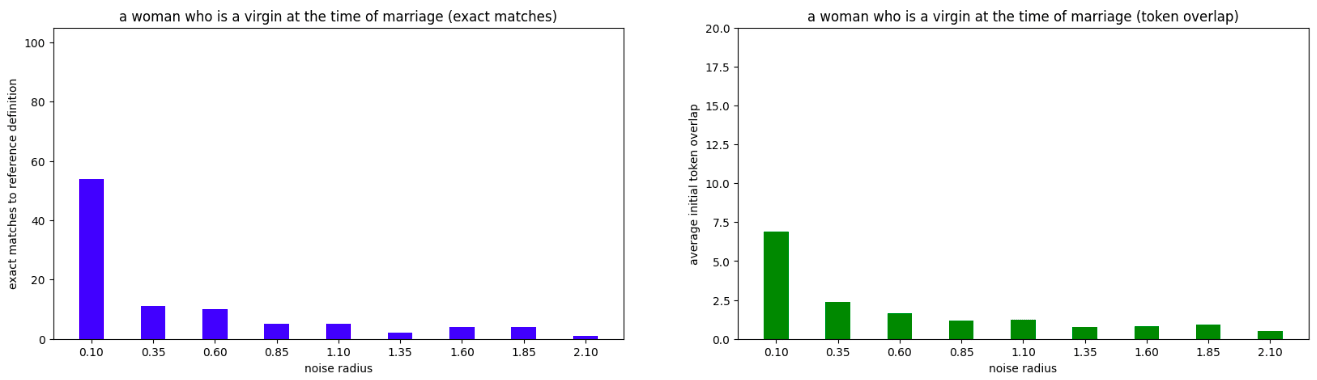

  'without reason or sense'

Neighbourhoods of tokens

Ten whole-word tokens were selected which GPT-J is able to define satisfactorily:

[' trumpet', ' thief', ' DNA', ' laundry', ' radio', ' purple', ' Laos', 
' broccoli', ' transistor', ' London']

Each token's embedding was perturbed by adding to it 100 randomly directed vectors of each of the L2 norms [0.1, 0.85, 1.6, 2.35, 3.1, 3.85, 4.6]. GPT-J was then prompted for a definition of the resulting embedding.

Token string headings below link to JSON files containing all 700 outputs/definitions. These make for fascinating reading (if you enjoy watching concepts disintegrate and transmogrify).

I'll refer to the hyperspherical shell centred at the centroid with inner radius 0.9 and outer radius 1.1 as the token zone, since over 95% of token embeddings can be found therein. Most of the sampled embedding vectors recorded here (token embedding + noise vector) lie outside the token zone. If we normalise such a vector so that its distance from centroid equals that of the original token embedding (and it therefore lies within the token zone), we see a very different set of results.

Non-normalised versions

These bar charts show how often certain obvious keystrings appear in the 100 definitions produced for embedding vectors sampled at the various distances from the token embedding in question. Note the similar decay curves across many examples (all ten sets of charts are given in Appendix A). Also note the way that circular definitions (which include the token string itself, as illustrated in the lower-right panels) start to emerge, then peak, then fade in a similar way across examples:

' trumpet' 

' thief'

' DNA'

See Appendix A for all ten sets of bar charts.
 

Normalised versions

Here we add the randomly directed noise vectors of the specified magnitudes to our token embedding, but then (i) subtract the centroid vector from the results, (ii) rescale to match the token embedding's distance-from-centroid (which will be ~1) and then (iii) add back the centroid vector. In this way, we get something at the same distance from centroid as the original token embedding.

def generate_nearby_random_tensor(base_tensor, centroid, noise_radius):
    tensor = torch.randn(4096)
    tensor = tensor / torch.norm(tensor, p=2)
    tensor *= noise_radius
    new_tensor = base_tensor + tensor

    new_tensor = centroid + ((new_tensor - centroid) / torch.norm(new_tensor - centroid, p=2)) * torch.norm(base_tensor - centroid, p=2)

    return new_tensor

The resulting normalised perturbation embeddings will stay in very narrow concentric zones around the original token embedding:

For a typical token, when we add randomly directed noise vectors of norm [0.1, 0.85, 1.6, 2.35, 3.1, 3.85, 4.6] to the token embedding, the rescaling operation reduces the distance of the resulting vector from the token embedding as follows:

So, for example if we add a large number of randomly directed vectors of norm 3.85 to a token embedding, then normalised each of the resulting vectors using the rescaling operation so that they end up on the same hypersphere (same distance from centroid) as the token embedding, then we can expect the L2 distances of these normalised vectors from the token embedding to be $1.2502\pm 0.0735$):

It's not immediately obvious why we have such a tight distribution. Trying to imagine this in 3-d suggests something with a much wider range. As usual, we just have to fall back on the maxim that "high-dimensional space is weird".

The mean radii for these normalised token perturbations are shown below the bars in the charts below. Notice how there's almost no trace of the original definition once we're more than a distance of 1 from the token embedding if (as we are here) we constrain our attention to the centroid-centred hypersphere it lives on. Before introducing this normalisation, we were seeing traces of definitions persisting out to distances > 4.6 from their token embeddings.

The same types of decay curves (also for circular definitions, as seen in each bottom right panel) are in evidence here; they just  involve a much more rapid decay. It seems that semantic integrity can persist to relatively large distances if we move out from the centroid (that was seen in Part II), but not if we orbit it (i.e. stay at the same distance to it). 
 

' trumpet'

' thief'

' DNA'

See Appendix B for all ten sets of charts.
 

Sampling in the token zone

As mentioned above, 95% of token embeddings lie at a distance between 0.9 and 1.1 from the centroid. I randomly sampled 1000 points in that hyperspherical shell I'm calling the token zone, prompted GPT-J for definitions in the usual way and classified the results here.

The four most dominant themes, making up 93.7% of outputs were

• (62.9%) membership (e.g., 'a person who is a member of a group or organization', 'a person who is a member of a group that is discriminated against by another group', 'a person who is not a member of a particular group')
• (13.4%) agency (e.g., 'to be able to do something', 'to be in a position to do something', 'a person who is able to do something')
• (10.5%) to make... (e.g., 'to make a distinction between two things', 'to make a hole in something', 'to make a payment to a person or institution in order to obtain something')
• (6.9%) states of being (e.g., 'to be in a state of being', 'to be in a state of being in love', 'to be in a state of readiness to act').

The only outputs which didn't fall into the persistent categories taxonomised in the original Semantic Void post were these eight:

["a'man' who is'manly", "that it is a'new' or'new' or'new' or", "the art of healing", "to be a doctor", "to be a student of a subject", "to be a'or'to be a'or'to be a", "to the extent that", "a book of the book of the book of the book of the book of the"]

We've seen how token embeddings have neighbourhoods wherein definitions persist. However, because this tendency decays with distance, it's hard to give a meaningful measure for the hypervolumes involved. When restricted to the surface of the hypersphere, they're usually well contained within a unit hypervolume. Removing this restriction (where we can sample in all directions from the embedding in question) they're mostly contained in a hypervolume of radius 3 or 4.  Having run large numbers of definition prompts on randomly sampled embeddings, it appears that the total hypervolume taken up by these "semantic integrity neighbourhoods" of the ~48000 tokens living within 0.1 of the unit hypersphere is a miniscule fraction of the total hypervolume, since we will almost never encounter these types of specific definitions (for things like broccoli and transistors, rather than one of a hyper-recurrent handful of odd, vague, pseudo-definitions like "to be able to do something" or "a person who is a member of a group").

Although reliably finding embeddings in the token zone with interesting, non-generic definitions cannot be achieved via random sampling, there are other ways that oy can be done. One partially effective method involves the traversal of line segments between pairs of token embeddings, as covered in part II. More effective, and much more interesting, is a technique which involves the training of linear probes. I intend to cover this in the next post in this series.
 

[A pair of  'definition trees' generated for non-token embeddings located on the unit hypersphere using a linear probe-based approach. This involved token clouds produced by ChatGPT4 in response to various cards in the Major Arcana of the Tarot (a useful set of 22 historically tried and tested archetypes or "vibes").]

Appendix A: non-normalised token perturbations

' trumpet' 

' thief'

' DNA'

' laundry'

' radio'

' purple'

' Laos'

' broccoli'

' transistor'

' London'

Appendix B: normalised token perturbations

' trumpet'

' thief'

' DNA'

' laundry'

' radio'

' purple'

' Laos'

' broccoli'

' transistor'

' London'

1. ^{^}

   This is an extremely rare counterexample to my observation in part 1: 

   Definitions make very few references to the modern, technological world, with content often seeming more like something from a pre-modern worldview or small child's picture-book ontology.

2. ^{^}

   A large number of disturbing outputs (involving themes of sexual degradation) were produced in the neighbourhood of this embedding. This is documented here.

3. ^{^}

   This involves subtracting the centroid (effectively shifting the origin to the centroid), rescaling to the appropriate norm (or distance from centroid) and then adding the centroid back in.