- August 23, 2023
Version 1.0.0
Abstract: In this article, I examine the discrepancies between classical game theory models and real-world human decision-making, focusing on irrational behavior. Traditional game theory frames individuals as rational utility maximizers, functioning within pre-set decision trees. However, empirical observations, as pointed out by researchers like Daniel Kahneman and Amos Tversky, reveal that humans often diverge from these rational models, instead being influenced by cognitive biases, emotions, and heuristic-based decision making.
Introduction
Game theory provides a mathematically rigorous model of human behavior. It has been applied to fields as diverse as Economics and literary Critical Theory. Within game theory, people are represented as rational actors seeking to maximize their expected utility in a variety of situations called "games." Their actions are represented by decision trees whose leaves represent outcomes labeled with utility values and whose nodes represent decision points. Game theory tells us how to back-propogate these leaf values to assign intermediate values to each node. These intermediate node values represent the expected utility of the associated situation. Game theory then tells us how to map these decision trees onto other representations, such as matrices; defines a taxonomy of standard games; and provides methods for determining the optimal strategies available to actors within these situations.
Unfortunately, for all of its mathematical elegance, game theory does not accurately model human behavior. As researchers such as Daniel Kahneman and Amos Tversky have pointed out, people are not rational utility maximizers. Instead, people rely on heuristics that are, at best, approximately logical and exhibit emotionality that leads them to act differently than game theory would predict. Over the years, these researchers have developed myriad alternative models to represent human decisions. This line of work has given rise to Behavioral Economics, which explores the economic consequences of this divergence from classical theory.[1]
While alternative models to classical game theory are valuable, I believe that there may be value in returning to classical game theory and seeing if there are natural extensions to these models that can account for some of the irrationality present in human decision making. In this brief technical note, I present some of my ideas.
Classical Game Theory
In classical game theory, we represent a person's decision space using a decision tree. The leaves of which represent potential end states. While the internal nodes represent decision points. We assign a utility value to each leaf that indicates how desirable (or undesirable) the associated outcome is. We then recursively back-propogate these leaf utility values back through the tree assigning intermediate values to each node. How we do this exactly depends on the type of situation being represented.
If the situation is a competition, then we have to assign two utility values to each leaf, one for each person. Each level within the tree represents the alternating decisions of each person. We then assume that each person chooses the course of action that maximizes their expected outcome from the state represented by the given node provided that the node represents a decision point for them.
Alternately, the situation could be one where the outcome of each decision is random. In this case, all of the nodes represent the decisions of a single person, but we associate a probability with each edge that represents the probability of reaching this state/outcome. In this case, the expected value of each node corresponds to the expected value of the outcomes that follow from that node's state.
Of course, nothing stops us from combining these types of models, we can easily construct decision trees that are both competitive and include random outcomes. Once we have modeled a situation using a decision tree, Game theory tells us how to find optimal solutions to them and tells us how rational agents will behave.
Working Example
It's easier to think about game theory when you have a concrete example. So, for the rest of this article, we will consider the following scenario in which a person is confronted by a police officer and is afraid of being arrested. They have three options available to them. They can argue with the cop and try to persuade them to let them go. Alternately, they can flee and run for it. Lastly, they can surrender. Ideally, they would prefer to be let go. Failing that, they would prefer to escape. The worst option for them is to be captured after trying to flee. Conversely, the best case for the cop is for the person to surrender, following that, they can put up with arresting them as they argue back. The worst case is for them to escape, which is closely followed by having to capture them. This situation can be represented by the following decision tree.
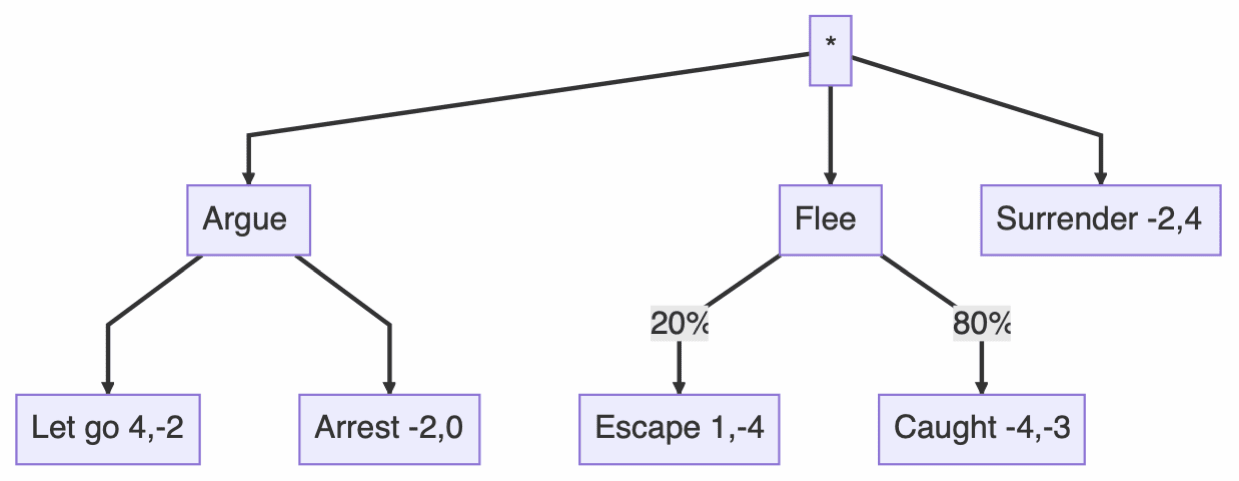
We have labeled each leaf with the utility value that each outcome has for the two people. For instance, we have labeled the "Let go" outcome as having value 4 for the person hoping to be let go, whereas, it has a value of -2 for the cop. If the person tries to flee, we assume that the cop will try to capture them. The outcome is uncertain however. The person has a 20% chance of successfully running away and an 80% chance of being seized. Accordingly, we have labeled the two edges leading to these outcomes with the corresponding probabilities.
Now, we can back-propagate expected utility values through the tree. Doing so, results in the following expected utility values:
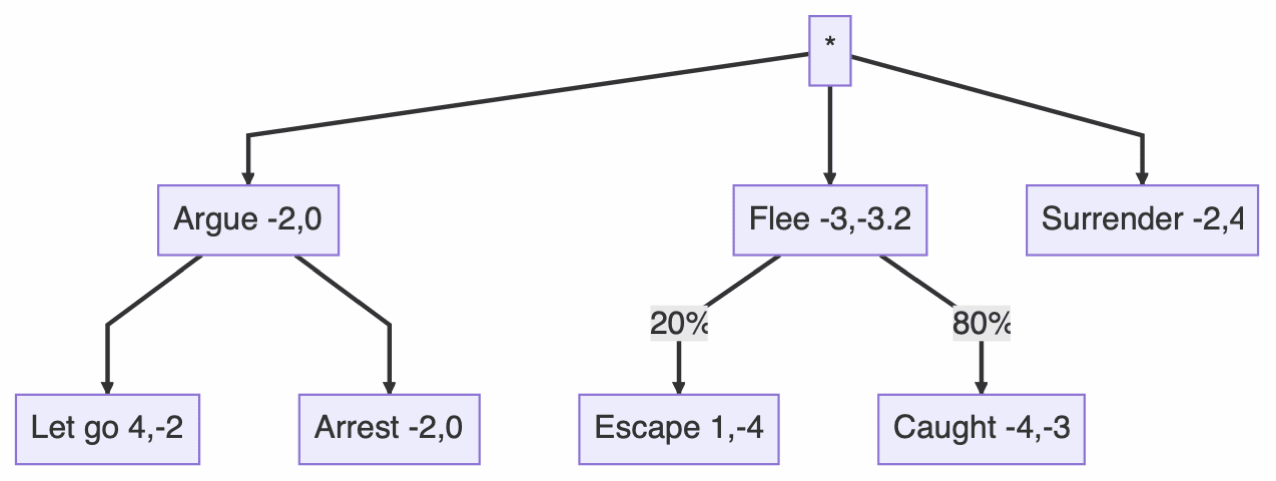
We can see that arguing has an expected value of -2 for the person fearing arrest because the cop, forced to choose between letting them go and arresting them, will prefer to arrest them. If the person attempts to flee, they have a 20% chance of escaping and an 80% chance of being caught. Hence, their expected utility value is. A similar calculation gives the expected utility for the cop. Game theory predicts that the person will be indifferent toward arguing and surrendering as both of these strategies have equal expected utility values and together they offer the best possible outcome.
In reality however, people act irrationally. Fear may compel them to flee or to surrender. A failure to think ahead might lead them to prefer running away or arguing to surrendering. Game theory doesn't factor in either of these tendencies. In the rest of this note, we extend game theory to include these factors.
Discernment
Whenever one course of action has a greater expected utility than all others, Game theory predicts that rational actors will always select it. However, people do not behave in this manner. Whenever a group of people are presented with a set of options, there is always someone who will choose an apparently irrational option. What's more, the more similar the expected benefit of two options are, the more people will choose the suboptimal one. Therefore, rather than selecting one option from a set, a mathematical theory of human decision making should assign probabilities to them.
Intuitively, this theory should assign equal probabilities to options that have the same expected utility. Given two options, where one strongly dominates the other, we would expect the probabilities to favor the better option. The following model has these two attributes.
Let's say that a person has two options and with expected utilities and . Then the probability that they will choose over is given by:
where represents "rational discernment" - the ability to discriminate between two options that have different expected utilities. This sigmoidal function has the desired behavior. It's when the two course of actions have the same expected utility - indicating indifference, it converges to 1 as the difference in expected utility tends toward , and it converges to 0 as the differences tends toward .
Let and be two options. Let specify the number of times that a person chooses an option. And, let represent the proportion of the time that they choose either or . Then, in instances, they will choose between and . Accordingly:
Equating both equations, we get:
which we can rearrange to produce:
Here, tells us how much more frequently the person chooses than .
Let represents the probability that the person will choose . Then:
We can use the likelihood ratios to write the following series of equations:
Each of these equations are easily solvable. For example:
Using these equations, we can now take a set of options that have expected utility values and define a probability distribution over them that specifies how likely a person is to choose each one of them.
Let's return to our running example and see how discernment might influence behavior. As we saw earlier, classical game theory predicts that that a person will always choose the optimal strategy. In the given scenario, game theory predicts indifference between arguing and surrendering, but our person will never flee. In contrast, if we factor in discernment using the model described above, we see that the person has an equal chance of arguing and surrendering, and a lower, but nonzero chance, of trying to run away.
Let's assume that our person has a rational discernment factor of 1. Then, for every pair of actions and , we can compute the probability that the person will choose over :
We can then compute the likelihood ratios for every pair of actions:
We can then solve for the probability that our person will choose to argue , flee , or surrender :
As we would expect, our person is equally likely to argue or surrender, which agrees with Game theory's indifference between these two course of actions. However, we see that the person now has a small chance of fleeing, which accords with our observation that people occassionally behave irrationally and choose suboptimal strategies.
Failure to Think Ahead
Game theory assumes that people are perfectly rational. They are able to think ahead and rationally weigh every possible outcome that may follow from a given decision. In reality, we know that this is not how people behave. People inevitably overlook certain potential outcomes and tend to fixate on others. How might we extend classical game theory to account for this observed behavior?
One option is to discount outcomes that are buried deeper within a decision tree. This models the fact that people have difficulty thinking ahead. In general, we cannot map out every possible consequence and we find drawn out logical chains difficult to follow. Mathematically, we multiply the utility values in our decision tree by a constant depth factor . Hence, outcomes at a depth will be discounted by a factor of .[2]
Let's set and apply this look ahead factor to our running example. Doing so, we get:
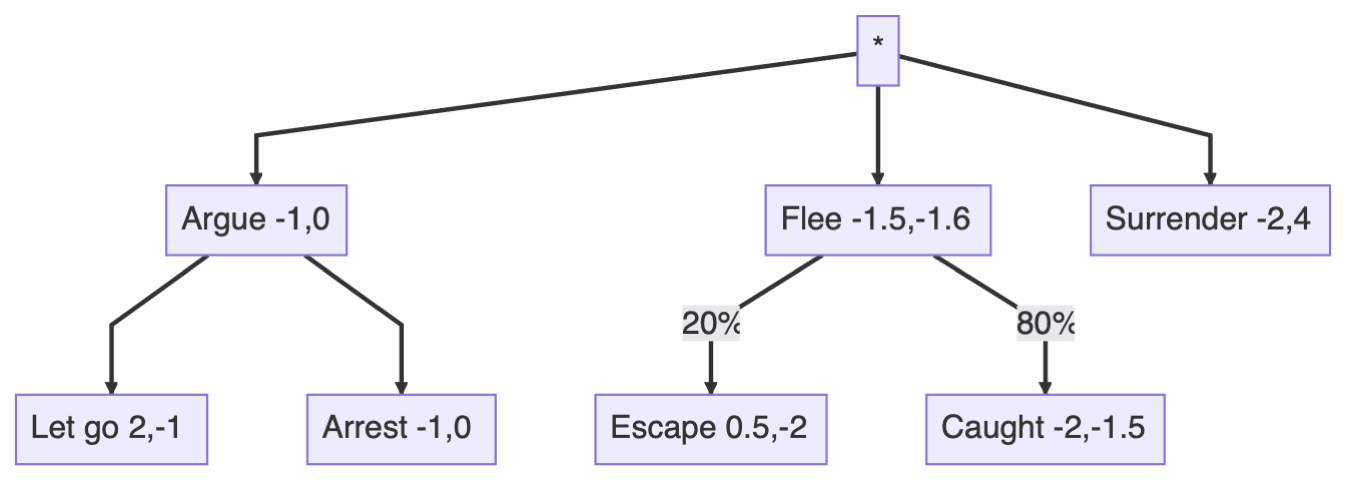
We see that our expected utility values change dramatically. Whereas game theory predicted that the person would be indifferent between surrendering and arguing, surrendering is now their worst option. Instead, failing to think ahead, they will choose almost anything to avoid and defer the immediate distress of being arrested. They will prefer to argue, and will even try to run away, before they will surrender.
Of course, we can combine the method we described above with the think ahead discount factor to calculate a probability distribution across these actions. Whereas traditional game theory predicts that everyone will now attempt to argue, our new method predicts that some some people will attempt to flee and that relatively few people will surrender outright. Setting we get:
Calculating the likelihood ratios, we find:
Finally, we can calculate the probability distribution over the course of actions: .
Emotional Urges
Humans are inherently emotional. Fear, anger, sadness, all serve to bias our reasoning, and each of them evoke atavistic urges. To a first degree approximation, we can identify two primary emotional effects. First, emotions bias our thoughts. Second, every emotion generates a characteristic set of urges. Anger spurs us to retaliate and aggress against those we believe have wronged us. Fear drives us alternately to flee or seek to control threatening situations. Sadness, saps motivation and chains us to numbed inactivity.
One way to represent these emotional urges is to define an urge vector for each emotion that assigns a probability to every course of action. We can then take the weighted average of these vectors based on the relative strength of a person's emotions. Lastly we take the average of the composite urge vector and the decision vector weighed by the person's emotionality.
Let's return to our running example and assume that a person seized by absolute fear will choose to argue, flee, and surrender according to the following probabilities:
A person panicking will flee of the time and will surrender of the time. Similarly, when enraged, let's assume that they will act according to the following probabilities:
This means that, the angrier they are, the more likely they are to argue and protest their arrest regardless of the consequences. Next, let's assume that our person is feeling an emotion that is fear and anger. In this case, their composite urge vector will be:
Lastly, let's assume that the person has an emotionality coefficient of . We then take the average between this urge vector and the decision vector weighted by the emotionality coefficient. Then, we can compute our final action probability as:
As expected, our person is more likely to try to run away because they are afraid and feel an urge to escape.
Emotional Fixation
As mentioned earlier, emotions compel us to fixate on certain scenarios and to overlook others. We can model this by assigning an emotional salience factor to various outcomes and multiplying outcome utility values by these factors according to the strength of the person's associated emotion.
Fear draws our attention to threatening scenarios; anger, to outcomes in which we are wronged. Sadness is different in that it renders us indifferent to future outcomes and latches our thoughts to past events. Still, we can model this "fixation" effect by associating an emotional bias vector with each emotion. This bias vector assigns a weight to every outcome. The sum of these weights must equal 1 so that the vector acts as a filter drawing attention to some outcomes at the expense of others.
We average these bias vectors according to the strength of the various emotions that a person feels. Then, we multiply the outcome utility values by the weights in the resulting composite vector to determine the emotionally weighted values of these outcomes.
We can illustrate this process using our running example. There are four potential outcomes: "let go," "arrested," "seized," and "escaped." Let's assume that anger fixates on them as follows:
This says that anger prompts our person to fixate on those scenarios in which they are seized and arrested and to overlook those in which they escape or are let go. These two outcomes have the greatest potential to elicit anger, resentment, and indignation, so it's natural to assume that an angry person would fixate most on them. We can define a similar vector for fear:
In this case, the person is most afraid of being seized and arrested. Fleeing may provoke the cop and the person is likely to fear retaliation. On the other hand, they may hope that they can flee the situation and escape from danger.
Let's assume again that our person is feeling a combination of emotions that are fear and anger. Then, they will have a composite bias vector of:
Lastly, let's assume that the person has an emotionality coefficient of . Let represent the emotionally biased utility value of outcome . Then we weight the utility values of each outcome according to:
This equation has two desirable features. First, when the emotionality coefficient equals 0, the utility values are not altered. Second, when equals one, the person's thoughts are completely "fixated" on those outcomes that are most salient:
Applying this formula to our running example, we find that the decision tree becomes:

I've updated the expected utility values for the person facing arrest. As before, we can calculate the probability that our person will choose each action.
Conclusion
In this technical note, I've described ways to extend classical Game theory to model aspects of human behavior that classical theory overlooks. I've presented, what I hope are simple and natural extensions that encapsulate elements of human irrationality stemming from our emotionality and cognitive limits. These extensions can be used to create mathematical models of human behavior that are qualitatively more "realistic" by including human traits such as near-sightedness, poor judgement, impulsivity, and emotional bias. While none of these models have been tested against actual human behavior, and may not accurately model real behavior, they may still have value by *qualitatively* modeling critical aspects of human behavior. In the same way that game theory's model of humans as rational agents has proven inaccurate but useful, these models of humans as quasi-rational emotional agents may prove insightful.
References
- ^
Prospect theory is a behavioral model that shows how people decide between alternatives that involve risk and uncertainty (e.g. % likelihood of gains or losses). It demonstrates that people think in terms of expected utility relative to a reference point (e.g. current wealth) rather than absolute outcomes.
- ^
Increased emotionality decreases our ability to think ahead. This could be modeled by making the rational discernment factor and the discount factor functions of the emotionality coefficient . Such a function should increase and as increases. For example, we may be able to represent both and as exponential functions of along the lines of .
I miss something about evolutionary game theory, where some of the discrepancies can be rationalized.
I wrote this tour from game theory to cultural evolution:
https://www.lesswrong.com/posts/xajeTjMtkGGEAwfbw/the-evolution-towards-the-blank-slate