Ideas of the Gaps

[-]rime2y50

Sometimes they're the same thing. But sometimes you have:
An unpredictable process with predictable final outcomes. E.g. when you play chess against a computer: you don't know what the computer will do to you, but you know that you will lose.
(gap) A predictable process with unpredictable final outcomes. E.g. if you don't have enough memory to remember all past actions of the predictable process. But the final outcome is created by those past actions.

Quoting E.W. Dijkstra quoting von Neumann:

...for simple mechanisms, it is often easier to describe how they work than what they do, while for more complicated mechanisms, it is usually the other way around.

Also, you just made me realise something. Some people apply the "beliefs should pay rent" thing way too stringently. They're mostly interested in learning about complicated & highly specific mechanisms because it's easier to generate concrete predictions with them. So they overlook the simpler patterns because they pay less rent upfront, even though they are more general and a better investment long-term.

For predictions & forecasting, learn about complex processes directly relevant to what you're trying to predict. That's the fastest (tho myopic?) way to constrain your expectations.

For building things & generating novel ideas, learn about simple processes from diverse sources. Innovation on the frontier is anti-inductive, and you'll have more success by combining disparate ideas and iterating on your own insights. To combine ideas far apart, you need to abstract out their most general forms; simpler things have fewer parts that can conflict with each other.

[-]Q Home2y10

So they overlook the simpler patterns because they pay less rent upfront, even though they are more general and a better investment long-term.

...

And if you use this metaphor to imagine what's going to happen to a tiny drop of water on a plastic table, you could predict that it will form a ball and refuse to spread out. While the metaphor may only be able to generate very uncertain & imprecise predictions, it's also more general.

Can you expand on the this thought ("something can give less specific predictions, but be more general") or reference famous/professional people discussing it? This thought can be very trivial, but it also can be very controversial.

Right now I'm writing a post about "informal simplicity", "conceptual simplicity". It discusses simplicity of informal concepts (concepts not giving specific predictions). I make an argument that "informal simplicity" should be very important a priori. But I don't know if "informal simplicity" was used (at least implicitly) by professional and famous people. Here's as much as I know: (warning, controversial and potentially inaccurate takes!)

Zeno of Elea made arguments basically equivalent to "calculus should exist" and "theory of computation should exist" ("supertasks are a thing") using only the basic math.
The success of neural networks is a success of one of the simplest mechanisms: backpropagation and attention. (Even though they can be heavy on math too.) We observed a complicated phenomenon (real neurons), we simplified it... and BOOM!
Arguably, many breakthroughs in early and late science were sealed behind simple considerations (e.g. equivalence principle), not deduced from formal reasoning. Feynman diagram weren't deduced from some specific math, they came from the desire to simplify.
Some fields "simplify each other" in some way. Physics "simplifies" math (via physical intuitions). Computability theory "simplifies" math (by limiting it to things which can be done by series of steps). Rationality "simplifies" philosophy (by connecting it to practical concerns) and science.
To learn flying, Wright brothers had to analyze "simple" considerations.
Eliezer Yudkowsky influenced many people with very "simple" arguments. Rational community as a whole is a "simplified" approach to philosophy and science (to a degree).
The possibility of a logical decision theory can be deduced from simple informal considerations.
Albert Einstein used simple thought experiments.
Judging by the famous video interview, Richard Feynman likes to think about simple informal descriptions of physical processes. And maybe Feynman talked about "less precise, but more general" idea? Maybe he said that epicycles were more precise, but a heliocentric model was better anyway? I couldn't find it.
Terry Tao occasionally likes to simplify things. (e.g. P=NP and multiple choice exams, Quantum mechanics and Tomb Raider, Special relativity and Middle-Earth and Calculus as “special deals”). Is there more?
Some famous scientists weren't shying away from philosophy (e.g. Albert Einstein, Niels Bohr?, Erwin Schrödinger).

Please, share any thoughts or information relevant to this, if you have any! It's OK if you write your own speculations/frames.

[-]rime2y10

I've taken to calling it the 'Q-gap' in my notes now. ^^'

You can understand AlphaZero's fundamental structure so well that you're able to build it, yet be unable to predict what it can do. Conversely, you can have a statistical model of its consequences that lets you predict what it will do better than any of its engineers, yet know nothing about its fundamental structure. There's a computational gap between the system's fundamental parts & and its consequences.

The Q-gap refers to the distance between these two explanatory levels.

...for simple mechanisms, it is often easier to describe how they work than what they do, while for more complicated mechanisms, it is usually the other way around.

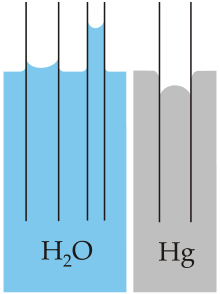
Let's say you've measured the surface tension of water to be 73 mN/m at room temperature. This gives you an amazing ability to predict which objects will float on top of it, which will be very usefwl for e.g. building boats.

As an alternative approach, imagine zooming in on the water while an object floats on top of it. Why doesn't it sink? It kinda looks like the tiny waterdrops are trying to hold each others' hands like a crowd of people (h/t Feynman). And if you use this metaphor to imagine what's going to happen to a tiny drop of water on a plastic table, you could predict that it will form a ball and refuse to spread out. While the metaphor may only be able to generate very uncertain & imprecise predictions, it's also more general.

By trying to find metaphors that capture aspects of the fundamental structure, you're going to find questions you wouldn't have thought to ask if all you had were empirical measurements. What happens if you have a vertical tube with walls that hold hands with the water more strongly than water holds hands with itself?^[1]

Beliefs should pay rent, but if anticipated experiences is the only currency you're willing to accept, you'll lose out on generalisability.

^{^}

^ capillary motion

LESSWRONG
LW

LESSWRONG
LW

4

4

4

Metrics

Complicated Ideas

Puzzles

Argumentation

Ideas as bits

Richness of ideas

Political gaps

Helping each other

Gaps of Alignment

Gaps of Taboo