The absurdity of the conclusion tells us rather forcefully that the rule is not always valid, even when the separate data values are causally independent; it requires them to be logically independent. In this case, we know that the vast majority of the inhabitants of China have never seen the Emperor; yet they have been discussing the Emperor among themselves and some kind of mental image of him has evolved as folklore. Then knowledge of the answer given by one does tell us something about the answer likely to be given by another, so they are not logically independent
Maybe it's just that it's late, but what he's saying in this quote isn't making sense to me.
To demonstrate the validity of the italicized comment, he should give an example where the data values are causally independent, but not logically independent. But the example he gives, of shared conversations and folklore, strike me as not causally independent at all, so while it supports the basic point about systematic error, it doesn't support this particular comment.
What's more, that's not even the problem. Let's say you ask the Chinese people to estimate the height of the king of Samoa. Here they've never talked of him, and know nothing about him other than that he's human. You still can't magic the information out of repeated estimation.
I was confused about that too. I think he must mean conditionally causally independent, but then he has to say conditional on what.
Maybe he means that each interview of a citizen is causally independent, since interviewing one of them won't causally affect the answer of another.
You could analyze the interview as adding a perturbation to people's "pre" responses, and per jsalvatier's comment, say that those perturbations are conditionally independent, as conditioned by the pre responses.
But it's the independence of the response that matters, and it's not independent of the stories and folklore.
Maybe my confusion can be clarified by showing a case where you have logical dependence but causal independence. I'm not seeing it. Jaynes uses inferential reasoning using backward in time urn draws as his go to example for causal independence but logical dependence. But that still seems a case where there is shared causal dependence on the number and kinds of balls in the urn originally.
This leads to the unfortunate consequence that the likely error of N=10 is 0.017<x<0.64956 while for N=1,000,000 it is the similar range 0.017<x<0.33433
I'm trying to follow the argument in footnote 1, but I got stuck on the above sentence -- where did these values (especially the 0.017) come from?
Aren't there lots of cases where the systematic error is small relative to the random error? Medicine seems like an example, simply because the random error is often quite large.
I actually would have said the opposite: medicine is one of the areas most likely to conduct well-powered studies designed for aggregation into meta-analyses (having accomplished the shift away from p-value fetishism into focusing on effect sizes and confidence intervals), and so have the least problem with random error and hence the most with systematic error.
Certainly you can't compare medicine with fields like psychology; in the former, you're going to get plenty of results from studies with hundreds or thousands of participants, and in the latter you're lucky if you ever get one with n>100.
Interesting. I did not know that medicine currently mostly does a good job of having well powered studies.
It would actually be pretty interesting, to go through many fields and determine how important systematic vs random error is.
Here's some guesses based on nothing more than my intuition:
What would you need to do this better? A sample of studies from prestigious journals for each field with N, size of random error, lower bound on effect size considered interesting.
Engineering - 10:1
Does engineering use these sorts of statistics? I read so few engineering papers I'm not really sure what statistics I would expect them to look like or how systematic vs random error would play out there.
A sample of studies from prestigious journals for each field with N, size of random error, lower bound on effect size considered interesting.
That would be an interesting approach; typically power studies just look at estimating beta, not beta and bounds on effect size.
If you read any narrow/weak/specific/whatever AI papers, then I'd say you do read engineering papers --- that's how I mostly think of my field, computational linguistics, anyway.
The "experiments" I'm doing at the moment are attempts to engineer a better statistical parser of English. We have some human annotated data, and we divide it up into a training section, a development section, and an evaluation section. I write my system and use the training portion for learning, and evaluate my ideas on the development section. When I'm ready to publish, I produce a final score on the evaluation section.
In this case, my experimental error is the extent to which the accuracy figures I produce do not correlate with the accuracy that someone really using my system will see.
Both systematic and random error abounds in these "experiments". I'd say a really common source of systematic error comes from the linguistic annotation we're trying to replicate. We evaluate on data annotated by the same people according to the same standards as we trained on, and the scientific standards of the linguistics behind that are poor. If some aspects of the annotation are suboptimal for applications of the system, that won't be reflected in my results.
From pg812-1020 of Chapter 8 “Sufficiency, Ancillarity, And All That” of Probability Theory: The Logic of Science by E.T. Jaynes:
Or pg1019-1020 Chapter 10 “Physics of ‘Random Experiments’”:
I excerpted & typed up these quotes for use in my DNB FAQ appendix on systematic problems; the applicability of Jaynes’s observations to things like publication bias is obvious. See also http://lesswrong.com/lw/g13/against_nhst/
If I am understanding this right, Jaynes’s point here is that the random error shrinks towards zero as N increases, but this error is added onto the “common systematic error” S, so the total error approaches S no matter how many observations you make and this can force the total error up as well as down (variability, in this case, actually being helpful for once). So for example,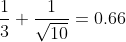 ; with N=100, it’s 0.43; with N=1,000,000 it’s 0.334; and with N=1,000,000 it equals 0.333365 etc, and never going below the original systematic error of
; with N=100, it’s 0.43; with N=1,000,000 it’s 0.334; and with N=1,000,000 it equals 0.333365 etc, and never going below the original systematic error of  . This leads to the unfortunate consequence that the likely error of N=10 is 0.017<x<0.64956 while for N=1,000,000 it is the similar range 0.017<x<0.33433 - so it is possible that the estimate could be exactly as good (or bad) for the tiny sample as compared with the enormous sample, since neither can do better than 0.017!↩
. This leads to the unfortunate consequence that the likely error of N=10 is 0.017<x<0.64956 while for N=1,000,000 it is the similar range 0.017<x<0.33433 - so it is possible that the estimate could be exactly as good (or bad) for the tiny sample as compared with the enormous sample, since neither can do better than 0.017!↩
Possibly this is what Lord Rutherford meant when he said, “If your experiment needs statistics you ought to have done a better experiment”.↩