Motivation
Löb's theorem is pretty counterintuitive. Speaking informally about one or more agents engaging in logically valid reasoning, the theorem says something like this:
- "If it's believed that believing a particular prophesy would cause it to self-fulfill, then the prophecy will be believed."
Formally, the theorem just says , where means " is provable". This is most weird if X is a false statement, because it means you can't prove that you can't prove X (Gödel's theorem).
(Also: the box symbol above is not an unrendered symbol; it's supposed to be a box.)
Meta-motivation
I'd like to make Löb's theorem more intuitive for humans, because it shows how agents can sidestep the need to mentally simulate each other in games, by instead using reasoning/arguments that happen to self-fulfill in a good and defensible way. Basically, Löbian reflection helps agents to avoid metacognitive stack overflows when thinking about themselves and each other, and I want more human beings to understand how that can work, and sometimes already does work, in real world agents.
State of the art
The best attempt I've seen to make Löb's theorem more intuitive is Eliezer Yudkowsky's Cartoon Guide to Löb's Theorem, which is still quite confusing. The confusingness comes from thinking about a self-referential statement ( on Wikipedia; S on Arbital) that's used to carry out the proof. The statement basically says "If this statement is provable, then C." Dealing with that sentence is pretty cumbersome, and requires a lot of fiddling around with nested statements and implications.
Doing better
I think we can make a new proof of Löb's theorem that doesn't use that weird self-referential sentence, by instead making the proof of Löb's theorem itself self-referential. Page 15 of the following paper poses an open problem on how to do this, which I think is possible to resolve affirmatively:
Here's a screenshot from it:

If we can make a proof like that work, we could then use the following much shorter and simpler cartoon guide to explain it:
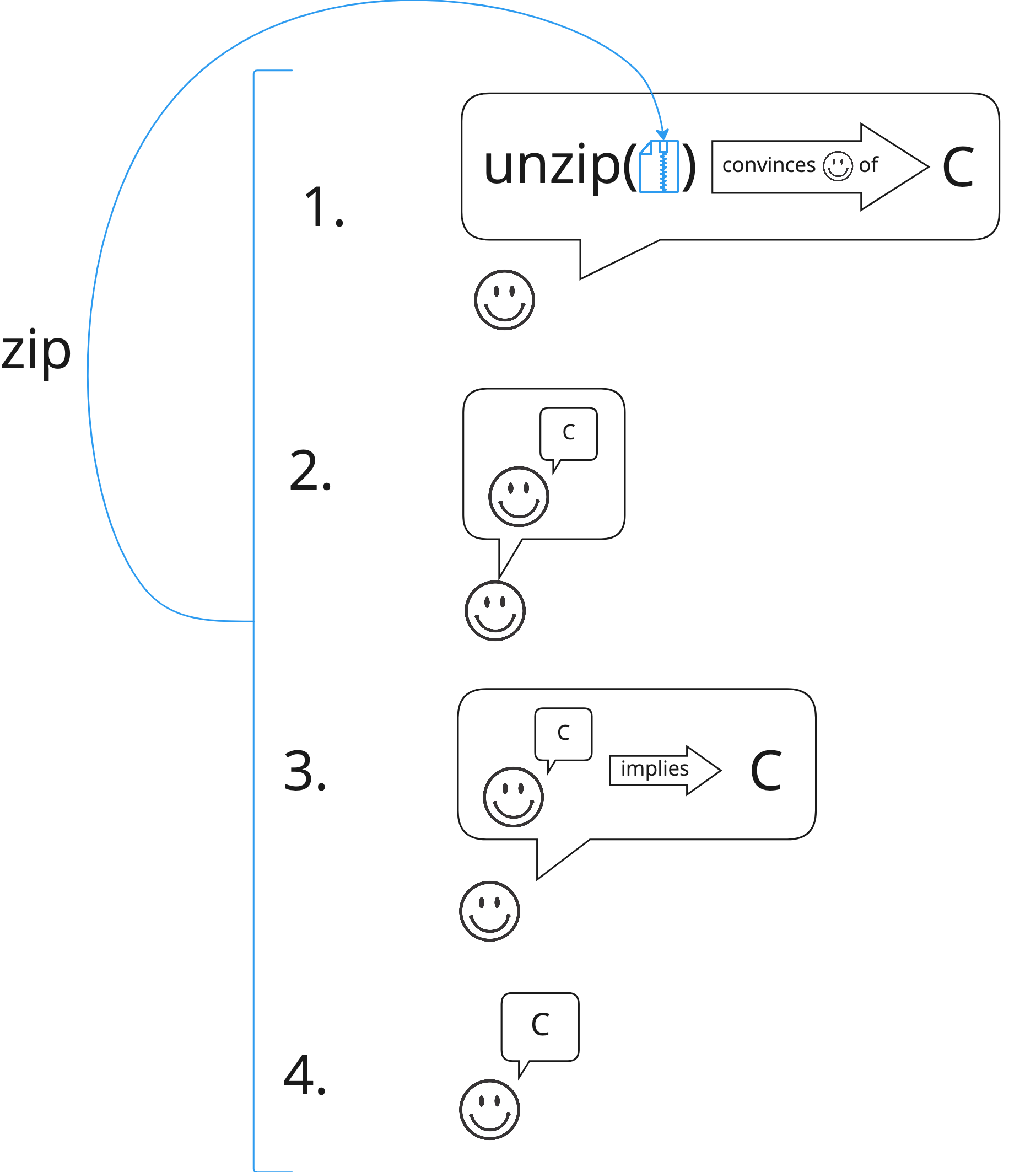
In other words, I want to write a proof of Löb's theorem that is structured much like a Quine. I'd like the details to (eventually) be really crisp and readable, so it can be peer reviewed for correctness, at a level of rigor comparable to this earlier paper on Löb's theorem for proof systems with bounded length:
As a possible start to writing such a proof, I think some of the same machinery (e.g., the diagonal lemma) from Boolos's textbook "The Logic of Provability" can be used to cook up self-referential proofs fitting the cartoon template above... thereby making Löb's theorem less mysterious and more intuitive forever.
Further meta-motivation (added Nov 26)
A key reason I'm interested in having a self-referential self-validating proof, rather than a normal-ish proof about a sentence that is self-referential (like on Wikipedia), is that human documents often refer to themselves, but human sentences rarely refer directly to themselves in isolation. This sentence is an exception, but such utterances are generally rare. So, making Löb more intuitive to humans either means
- making humans more accustomed to thinking about sentences that refer to themselves (so the traditional proof of Löb can be more intuitive), or
- finding a new proof that self-references in a way that's more like the way a human document refers to itself.
The aim of this post is to try for the second approach. Notice how you didn't think the previous sentence was weirdly self-referential? That's because it referred to the whole document that it's part of, rather than just narrowly referring directly to itself. I'm not quite sure why humans are more comfortable with that than with directly-and-narrowly self-referential sentences. Maybe it's because I thing needs to have enough non-self-referential content before humans will care about it enough to tolerate it talking about itself. I'm not sure.
Countering naive impossibility arguments (added Nov 26)
It's in fact possible to use Löb's theorem to construct a self-referential proof of the kind illustrated above. So, naive arguments that "Proofs can't be self-referential like that" are not going to hold up. The hard thing I'm asking for is to make such a proof — of Löb's theorem specifically — without going through the traditional proof of Löb, i.e., without using a narrowly-and-directly-self-referential sentence (like on Wikipedia).
Difficulty assessment
I think getting a Qunean proof to work here is probably a bit easier than the JSL paper linked directly above. Like, I think if I spent 3 months on it (which is how long the JSL paper took), then I could do it. I do think getting it right involves mentally syncing with some fundamental and standard machinery in provability logic, which can take a bit of time if you've never worked in the area before (as I hadn't).
Anyway, if you can figure out how to write this proof, please post your solution or solution attempts here :)


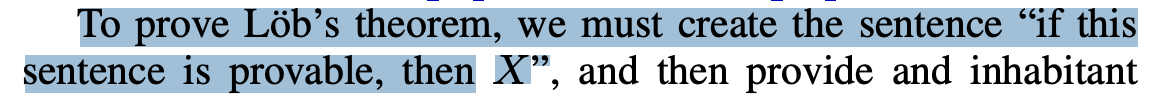
(Epistemic status: quickly-recounted lightly-edited cached state that I sent in response to an email thread on this topic, that I now notice had an associated public post. Sorry for the length; it was easier to just do a big unfiltered brain-dump than to cull, with footnotes added.)
here's a few quick thoughts i have cached about the proof of löb's theorem (and which i think imply that the suggested technique won't work, and will be tricky to repair):
#1. löb's theorem is essentially just the Y combinator, but with an extra level of quotation mixed in.[1]
the standard proof of löb's theorem (e.g. as it appears in the cartoon guide) is complicated by two points:
1a. one thing we need here is that the variable
sis sensical, and in particular we need some S withS ≃ (□ S → A). the existence of such an S follows from the diagonal lemma.[2]1b. the other thing we need here is to show that quotation and normal proof steps (function application or modus ponens or whatever) interact in the "obvious way", and don't gum each other up. for instance, we need that
□(A → B) ∧ □(A)yields□(B), showing that we can "apply quoted functions to quoted arguments", in order for syntax likef (s "s")to be sensical.if i were trying to make a guide to löb's theorem today, i'd break it down as above; for me, at least, this breakdown is significantly more intuitive than the cartoon guide (which, iirc, doesn't even go into the diagonal lemma, and just blends the Y combinator together with 1b).
this suggests that you're going to be hard-pressed to do any self-reference without routing through the nomal machinery of löb's theorem, in the same way that it's hard to do recursion in the lambda calculus without routing through the Y combinator--you don't need to use Y per se, but you're unlikely to find a simpler way to do generic recursion.
this also suggests that you're hiding all the work done by the normal proof of löb's theorem in the definition of "zip", and that this proof won't turn out to be simpler when "zip" is cashed out in full.
#2. fun fact: the diagonal lemma is also just an instance of the Y combinator with an extra level of quotation.
in fact, there's a proof of the diagonal lemma that goes by analogy to the proof-sketch of löb's theorem (above). very roughly speaking, the way that you avoid infinite regress is that, in the step 1a, you need an S with
S ≃ □ S → Type, and this S can be written manually because Type (or Proposition or w/e you want to use) is very rich (namely, it contains existential quantifiers and equality).[3]indeed, you can think of the diagonal lemma as simply an application of löb's theorem where the target A is Type (or Proposition or w/e).
in fact, this analogy is quite tight. one cool corollary is that we can pop open tarski's undefinability of truth, and replace the diagonal lemma with löb's theorem. the result is a new theorem that i call "the undefinability of normalization": no theory can prove that its terms normalize, on pain of contradiction.
(proof, in case it's not obvious: invoke löb's theorem on
(not ∘ normalize : □ Bool → Bool), now you have syntax for a boolean value that's provably-equal to its own negation.)#3. fun fact: löb's theorem does not hold for various breeds of normalized proofs (such as proofs with cuts eliminated--though exactly what counts as "normalized" in PA is somewhat subtle). in particular, when □ denotes normalized proofs,
□(A → B) ∧ □(A)does not yield□(B), because feeding a normalized argument into a normalized function does not yield a normalized output. and while we (who trust the theory) know that unnormalized-box(B) implies normalized-box(B), no consistent theory can prove its own version of that fact, by the undefinability of normalization!...which yields the hypothesis that the One True Counterfactuals are those facts which have short normalized proofs.
(recall: i think it was patrick who first set forth the trolljecture that counterfactuals correspond to short proofs of material implications? and this trolljecture was shot down by the existence of spurious counterfactuals, which use löb to deduce arbitrary material implications with a ~constant proof-length. but that counterexample doesn't apply to normalized proofs! so the repaired trolljecture yet stands!)
(though i admit this hasn't risen high enough in my priority-queue for me to actually try to prove nice things about this bold new notion of counterfactuals. also they obviously can't be the whole answer, b/c normalized proofs about large worlds are large, etc.)
slighly more formally: both the Y combinator and löb's theorem are instantiations of a generalization of lawvere's fixpoint theorem to semicategories. in the case of the Y combinator, we use some domain (in the sense of domain theory) that serves as semantics for the untyped lambda calculus. in löb's theorem, iirc we use a semicategory where a morphism from A to B is a proof of □ A → B (tho this is an old cached thought that i haven't checked). that the latter is not a category follows from gödel incompleteness; there's no identity morphism at ⊥.
note: i dislike semicategories, and if you have a more elegant way to unify Y and löb, i'm eager to hear it. ↩︎
in other words: the santa clause sentence is just the natural/obvious type of the variable in the Y combinator (as modified to work with gödel-codes). if you want a better intuition for it, i recommend the exercise of trying to figure out what type the variable
sshould have in the normal Y combinator. ↩︎in fact, according to me, this is one of three keys to löb's theorem.
the first two keys are ofc gödel-codes + the Y combinator, with the caveat that making the Y combinator behave requires the diagonal lemma.
and the diagonal lemma is again just gödel-codes + the Y combinator, except that in this very specific case we can make the Y combinator behave without already needing the diagonal lemma, by hand-coding in a workaround using quantifiers and equalities and whatnot.
and the hand-coded workaround is kinda hacky. very roughly speaking, the trouble is that we want to let
G(s)beF (s "s"), but showing thats "s"is sensical relies on the diagonal lemma, which we're in the middle of proving and can't invoke.and the solution is to let
G(s)instead be∃ x. just x = try (s "s") ∧ F x. we don't need to know thats "s"is sensical, because we're naming a proposition, and we can just bolt on a clause asserting thats "s"is sensical! we just build our sentence to say "s "s"is sensical, and also ...", and thus sidestep the problem!in other words: we're able to build a sentence that would be meaningful (it would mean a falsehood) even if
s "s"wasn't sensical, and this lets us form a sort of "guarded" version of the Y combinator (in the special case where we're producing a sentence) that doesn't depend critically on the sensicality ofs "s". (which ends up makings "s"be sensical in the actual use-case ofG "G", and so the guard ends up redundant and harmless.)(exercise: why can't you use this technique to avoid the invocation of the diagonal lemma from the proof of gödel's incompleteness theorem, i.e. löb's theorem where the target A is ⊥?)
this technique lets us slip around the need to invoke the diagonal lemma before we've finished proving the diagonal lemma. which is a critical step in the bootstrapping process.
...i don't have this point entirely distilled yet, but hopefully that gives at least some intuition for what i mean when i say that löb is just gödel-codes + the Y combinator + a hacky workaround to get you off the ground. ↩︎
(another thing that might help: when you're proving an implication □ C → C, the gödel-number that you're given doesn't code for the proof of the implication you're currently writing; that would be ill-typed. you asked for a □ C, not a □ (□ C → C). so the gödel-number you're given isn't a code for the thing you're currently writing, it's a code for löb's theorem applied to the thing you're currently writing.
it is for this reason that the proof you're fed might not be exactly the proof you were hoping for. you started out your implication being like "step 1:... (read more)