Comment Permalink

1mo31

Indeed, very interesting!

See in context

30 Estimating the Probability of Sampling a Trained Neural Network at Random

by Adam Scherlis

, Nora Belrose

1st Mar 2025

AI Alignment Forum

1 min read

30 Ω 16

This is a linkpost for https://arxiv.org/abs/2501.18812

(adapted from Nora's tweet thread here.)

Consider a trained, fully functional language model. What are the chances you'd get that same model -- or something functionally indistinguishable -- by randomly guessing the weights?

We crunched the numbers and here's the answer:

We've developed a method for estimating the probability of sampling a neural network in a behaviorally-defined region from a Gaussian or uniform prior.

You can think of this as a measure of complexity: less probable, means more complex.

Our method works by exploring random directions in weight space, starting from an "anchor" network that defines the behavior.

The distance from the anchor to the edge of the region, along the random direction, gives us an estimate of how big (or how probable) the region is as a whole.

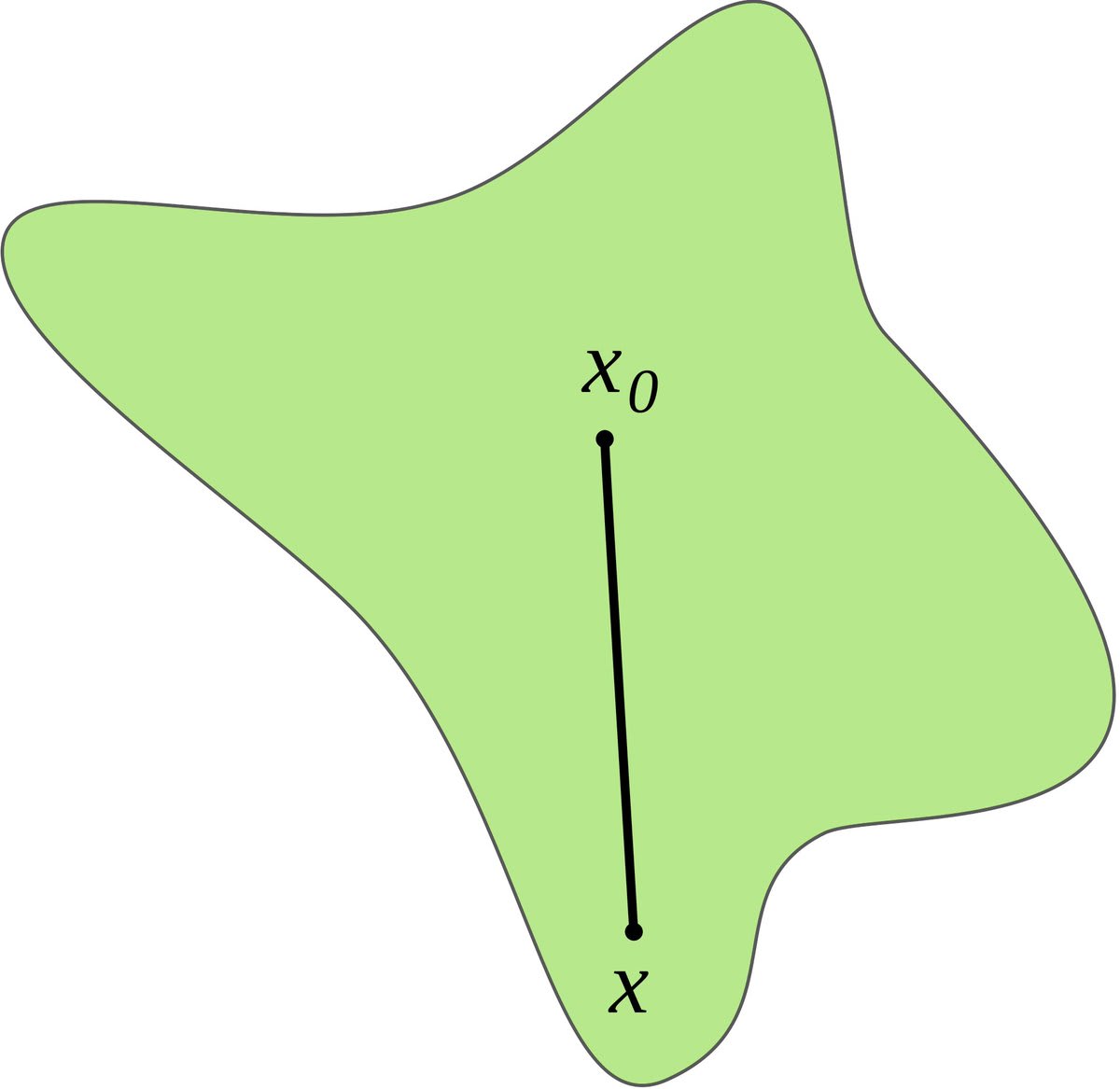
But the total volume can be strongly influenced by a small number of outlier directions, which are hard to sample in high dimension— think of a big, flat pancake.

Importance sampling using gradient info helps address this issue by making us more likely to sample outliers.

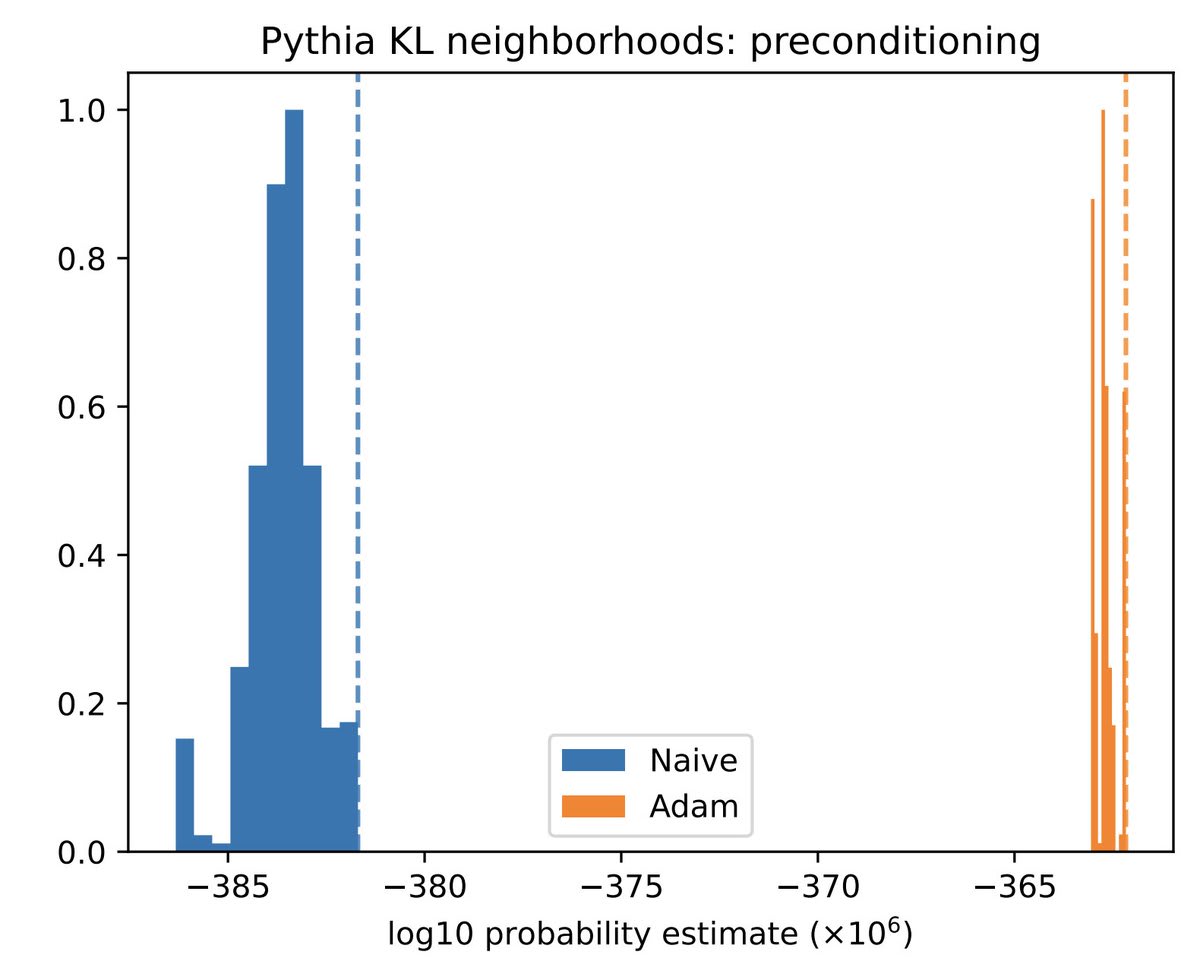
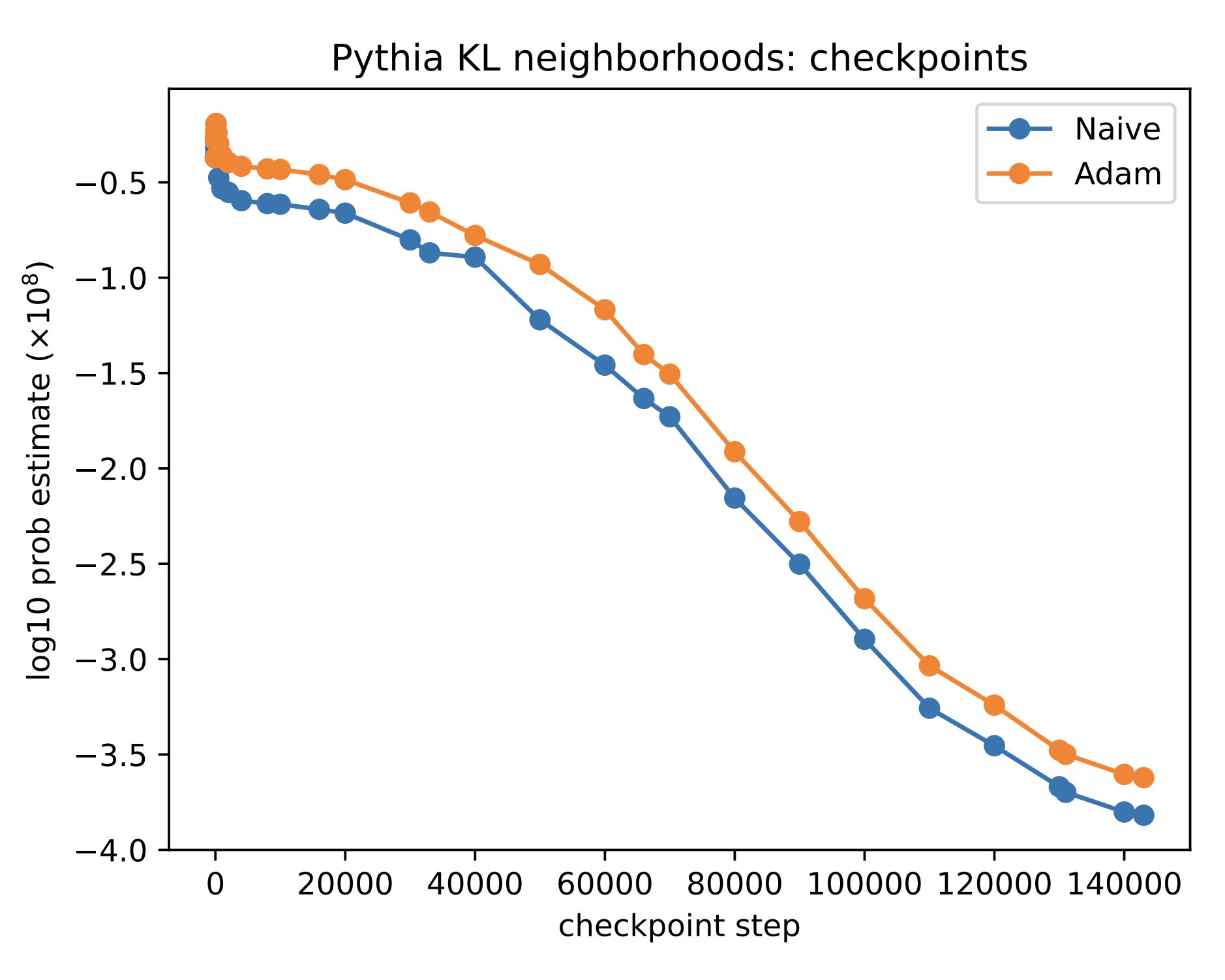
We find that the probability of sampling a network at random— or local volume for short— decreases exponentially as the network is trained and grows in complexity.

And networks which memorize their training data without generalizing have lower local volume— higher complexity— than generalizing ones.

We're interested in this line of work for two reasons:

First, it sheds light on how deep learning works. The "volume hypothesis" says DL is similar to randomly sampling a network from weight space that gets low training loss. (This is roughly equivalent to Bayesian inference over weight space.) But this can't be tested if we can't measure volume.

Second, we speculate that complexity measures like this can be useful for detecting undesired "extra reasoning" in deep nets. We want networks to be aligned with our values instinctively, without scheming about whether this would be consistent with some ulterior motive: https://arxiv.org/abs/2311.08379

Our code is available (and under active development) here.

Interpretability (ML & AI)Machine Learning (ML)Singular Learning TheoryAI

Frontpage

30 Ω 16

Estimating the Probability of Sampling a Trained Neural Network at Random

New Comment

9 comments, sorted by

top scoring

Click to highlight new comments since: Today at 1:27 PM

[-]Adam Scherlis

1mo50

If you're wondering if this has a connection to Singular Learning Theory: Yup!

In SLT terms, we've developed a method for measuring the constant (with respect to n) term in the free energy, whereas LLC measures the log(n) term. Or if you like the thermodynamic analogy, LLC is the heat capacity and log(local volume) is the Gibbs entropy.

We're now working on better methods for measuring these sorts of quantities, and on interpretability applications of them.

[-]Lucius Bushnaq

1mo50

'Local volume' should also give a kind of upper bound on the LLC defined at finite noise though, right? Since as I understand it, what you're referring to as the volume of a behavioral region here is the same thing we define via the behavioural LLC at finite noise scale in this paper? And that's always going to be bigger or equal to the LLC taken at the same point at the same finite noise scale.

[-]jacob_drori

25d21

Let be volume of a behavioral region at cutoff $ϵ$ . Your behavioral LLC at finite noise scale is $λ (ϵ) := d log V / d log ϵ$ , which is invariant under rescaling $V$ by a constant. This information about the overall scale of $V$ seems important. What's the reason for throwing it out in SLT?

[-]Lucius Bushnaq

25d51

Because it’s actually not very important in the limit. The dimensionality of V is what matters. A 3-dimensional sphere in the loss landscape always takes up more of the prior than a 2-dimensional circle, no matter how large the area of the circle is and how small the volume of the sphere is.

In real life, parameters are finite precision floats, and so this tends to work out to an exponential rather than infinite size advantage. So constant prefactors can matter in principle. But they have to be really really big.

[-]Adam Scherlis

10h10

I am not sure I agree :)

It is unimportant in the limit (of infinite data), but away from that limit, it is only unimportant by a factor of 1/log(data), which seems small enough to be beatable in practice in some circumstances.

The spectra of things like Hessians tend to be singular, yes, but also sort of power-law. This makes the dimensionality a bit fuzzy and (imo) makes it possible for absolute volume scale of basins to compete with dimensionality.

Essentially: it's not clear that a 301-dimensional sphere really is "bigger" than a 300-dimensional sphere, if the 300-dimensional sphere has a much larger radius. (Obviously it's true in a strict sense, but hopefully you know what I'm gesturing at here.)

[-]Adam Scherlis

10h10

I think this is correct but we're working on paper rebuttals/revisions, I'll take a closer look very soon! I think we're working along parallel lines.

In particular, I have been thinking of "measure volumes at varying cutoffs" as being more or less equivalent to "measure LLC at varying ε".

We choose expected KL divergence as a cost function because it gives a behavioral loss, just like your behavioral LLC, yes.

I can give more precise statements once I look at my notes.

[-]Daniel Murfet

1mo31

Indeed, very interesting!

[-]Lucius Bushnaq

1mo40

How does the performance of this compare to the SGLD sampling approach used by Timaeus, or to bounding the volume by just calculating the low-lying parts of the Hessian eigenspectrum? Or, to go even hackier and cheaper, just guessing the Hessian eigenspectrum with kfac-approximation by doing a PCA of the activations and gradients at every layer and counting the zero eigenvalues of those?

(For all of those approaches, I'd use the loss landscape/Hessian of the behavioural loss defined in section 2.2 of that last link, since you want to measure the volume of a behavioural region.)

[-]Oliver Daniels

1mo2-1

also rhymes with/is related to ARC's work on presumption of independence applied to neural networks (e.g. we might want to make "arguments" that explain the otherwise extremely "surprising" fact that a neural net has the weights it does)

Moderation Log