Comment Permalink

How can we know that "it is possible to train a 200 IQ equivalent intelligence for at most 3 MW-hr"?

5 Why the technological singularity by AGI may never happen

3rd Sep 2021

1 min read

5

Artificial general intelligence is often assumed to improve exponentially through recursive self-improvement, resulting in a technological singularity. There are hidden assumptions in this model which should be made explicit so that their probability can be assessed.

Let us assume that:

The Landauer limit holds, meaning that:
- Reversible computations are impractical
- Minimum switching energy is of order J per operation
- Thus, energy cost at $k T$ of order 1 EUR per $10^{22}$ FLOPs (details)
General intelligence scales sublinear with compute:
- Making a machine calculate the same result in half the time costs more than twice the energy:
  - Parallelization is never perfect (Amdahl's law)
  - Increasing frequency results in a quadratic power increase ( $P \propto f V^{2}$ )
- Similarly, cloning entire agents does not speed up most tasks linearly with the number of agents ("You can't produce a baby in one month by getting nine women pregnant.")
- Improving algorithms will have a limit at some point

My prior on (1) is 90% and on (2) about 80%.

Taken together, training ever larger models may become prohibitively expensive (or financially unattractive) for marginal gains. As an example, take an AGI with an intelligence level of 200 points, consuming 1 kW of power. Increasing its intelligence by a few points may come at 10x the power requirement. Mock visualization:

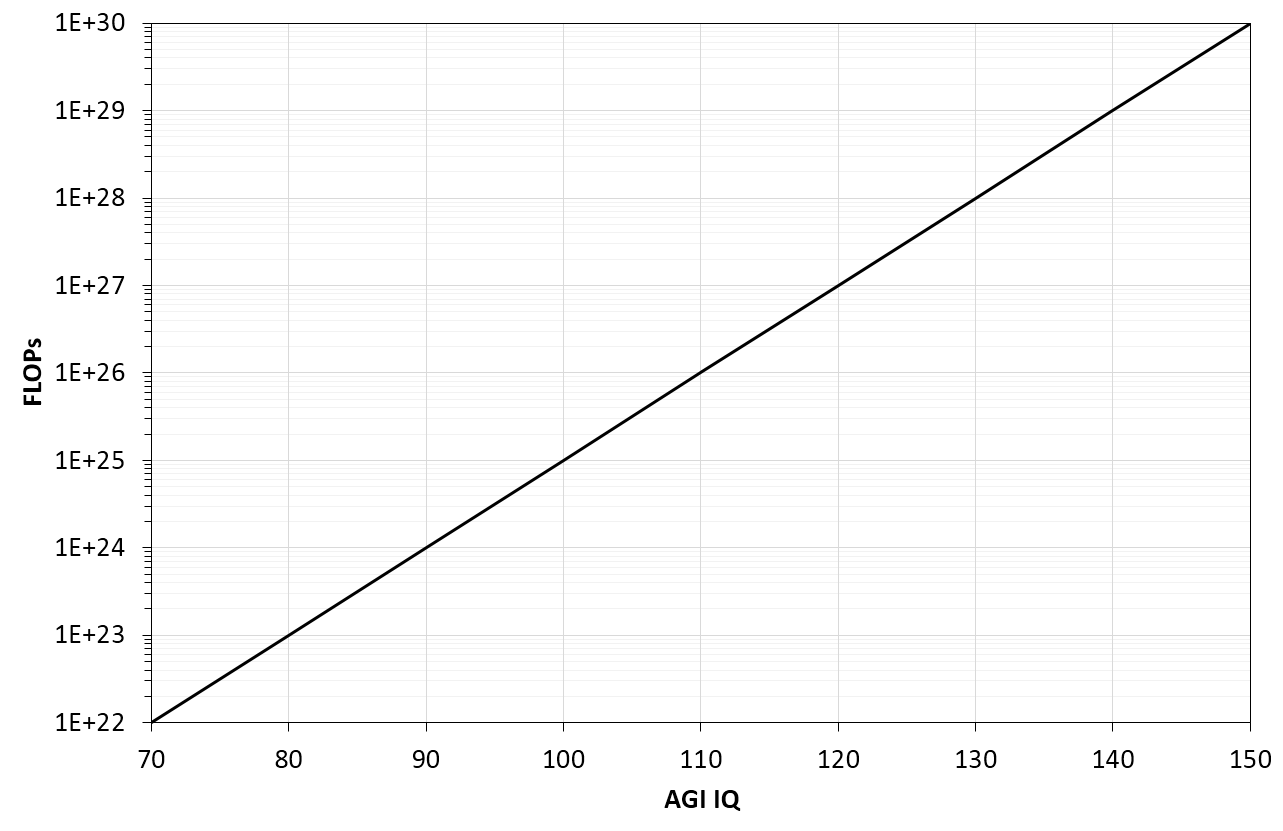
If these assumptions hold, then the exponential increase in capabilities would likely break down before a singularity is reached.

AI CapabilitiesAI RiskAI

Frontpage

5

Why the technological singularity by AGI may never happen

New Comment

14 comments, sorted by

top scoring

Click to highlight new comments since: Today at 8:47 PM

[-]Steven Byrnes4y150

I think your two assumptions lead to "the exponential increase in capabilities would likely break down at some point". Whereas you say "the exponential increase in capabilities would likely break down before a singularity is reached". Why? Hmm, are you thinking that "singularity" = "literally diverging to infinity", or something? In that case there's a much simpler argument: we live in a finite universe, therefore nothing will diverge to literally infinity. But I don't think that's the right definition of "singularity" anyway. Like, the wikipedia definition doesn't say "literally infinity". So what do you mean? Where does the "likely before a singularity" come from?

For my part, if there's a recursive-self-improvement thing over the course of 1 week that leaves human intelligence in the dust, and results in AI for $1/hour that can trounce humans in every cognitive domain as soundly as AlphaZero can trounce us at chess, and it's installed itself onto every hackable computer on Earth … well I'm gonna call that "definitely the singularity", even if the recursive-self-improvement cycle "only" persisted for 10 doublings beyond human intelligence, or whatever, before petering out.

Incidentally, note that a human-brain-level computer can be ~10,000× less energy-efficient than the human brain itself, and its electricity bills would still be below human minimum wage in many countries.

Also, caricaturing slightly, but this comment section has some arguments of the form:
A: "The probability of Singularity is <100%!"
B: "No, the probability of Singularity is >0%!"
A: "No, it's <100%!!" …
So I would encourage everyone here to agree that the probability is both >0% and <100%, which I am confident is not remotely controversial for anyone here. And then we can be more specific about what the disagreement is. :)

[-]Charlie Steiner4y70

Yep. But there's no reason to think humans sit on the top of the hill on these curves - in fact, humans with all their foibles and biological limitations are pretty good evidence that significantly smarter things are practical, not just possible.

I can't remember if Eliezer has an updated version of this argument, but see https://intelligence.org/files/IEM.pdf .

[-]jbash4y40

Assuming you had a respectable metric for it, I wouldn't expect general intelligence to improve exponentially forever, but that doesn't mean it can't follow something like a logistic curve, with us near the bottom and some omega point at the top. That's still a singularity from where we're sitting. If something is a million times smarter than I am, I'm not sure it matters to me that it's not a billion times smarter.

[-]hippke4y00

Sure! I argue that we just don't know whether such a thing as "much more intelligent than humans" can exist. Millions of years of monkey evolution have increased human IQ to the 50-200 range. Perhaps that can go 1000x, perhaps it would level of at 210. The AGI concept makes the assumption that it can go to a big number, which might be wrong.

[-]Dave Lindbergh4y40

We don't know, true. But given the possible space of limiting parameters it seems unlikely that humans are anywhere near the limits. We're evolved systems, evolved under conditions in which intelligence was far from the most important priority.

And of course under the usual evolutionary constraints (suboptimal lock-ins like backward wired photoreceptors in the retina, the usual limited range of biological materials - nothing like transistors or macro scale wheels, etc.).

And by all reports John von Neumann was barely within the "human" range, yet seemed pretty stable. He came remarkably close to taking over the world, despite there being only one of him and not putting any effort into it.

I think all you're saying is there's a small chance it's not possible.

[-]hippke4y20

How did von Neumann come close to taking over the world? Perhaps Hitler, but von Neumann?

[-]wunan4y30

Even without having a higher IQ than a peak human, an AGI that merely ran 1000x faster would be transformative.

[-]Quintin Pope4y30

I think this is plausible, but maybe a bit misleading in terms of real-world implications for AGI power/importance.

Looking at the scaling laws observed for language model pretraining performance vs model size, we see strongly sublinear increases in pretraining performance for linear increases in model size. In figure 3.8 of the GPT-3 paper, we also see that zero/few/many shot transfer learning to SuperGLUE benchmarks also scale sublinearly with model size.

However, the economic usefulness of a system depends on a lot more than just parameter count. Consider that Gorillas have 56% as many cortical neurons as humans (9.1 vs 16.3 billion; see this list), but a human is much more than twice as economically useful as a gorilla. Similarly, a merely human level AGI that was completely dedicated to accomplishing a given goal would likely be far more effective than a human. E.g., see the appendix of this Gwern post (under "On the absence of true fanatics") for an example of how 100 perfectly dedicated (but otherwise ordinary) fanatics could likely destroy Goldman Sachs, if each were fully willing to dedicate years of hard work and sacrifice their lives to do so.

[-]gwern4y80

Don't forget https://www.gwern.net/Complexity-vs-AI which deals with hippke's argument more generally. We could also point out that scaling is not itself fixed as constant factors & exponents both improve over time, see the various experience curves & algorithmic progress datasets. (To paraphrase Eliezer, the IQ necessary to destroy the world drops by 10% after every doubling of cumulative research effort.)

[-]JBlack4y10

The first two points in (1) are plausible from what we know so far. I'd hardly put it at more than 90% that there's no way around them, but let's go with that for now. How do you get 1 EUR per 10^22 FLOPs as a fundamental physical limit? The link has conservative assumptions based on current human technology. My prior on those holding is negligible, somewhere below 1%.

But that aside, even the most pessimistic assumption in this post don't imply that a singularity won't happen.

We know that it is possible to train a 200 IQ equivalent intelligence for at most 3 MW-hr, energy that costs at most $30. We also know that once trained, it is possible for it to do at least the equivalent of a decade of thought by the most expert human that has ever lived for a similar cost. We have very good reason to expect that it could be capable of thinking very much faster than the equivalent human.

Those alone are sufficient for a superintelligence take-off that renders human economic activity (and possibly the human species) irrelevant.

[-]hippke4y30

How can we know that "it is possible to train a 200 IQ equivalent intelligence for at most 3 MW-hr"?

[-]JBlack4y30

Because 20-year-old people with 200 IQ exist, and their brains consume approximately 3 MW-hr by age 20. Therefore there are no fundamental physical limitations preventing this.

[-]hippke4y30

I think this calculation is invalid. A human is created from a seed worth 700 MB of information, encoded in the form of DNA. This was created in millions of years of evolution, compressing/worth a large (but finite) amount of information (energy). A relevant fraction of hardware and software is encoded in this information. Additional learning is done during 20 years worth 3 MWh. The fractional value of this learning part is unknown.

[-]JBlack4y10

Initialising a starting state of 700 MB at 10^-21 J per bit operation costs about 6 picojoules.

Obtaining that starting state through evolution probably cost many exajoules, but that's irrelevant to the central thesis of the post: fundamental physical limits based on the cost of energy required for the existence of various levels of intelligence.

If you really intended this post to hypothesize that the only way for AI to achieve high intelligence would be to emulate all of evolution in Earth's history, then maybe you can put that in another post and invite discussion on it. My comment was in relation to what you actually wrote.

Moderation Log