"Heretical Thoughts on AI" by Eli Dourado
Abstract Eli Dourado presents the case for scepticism that AI will be economically transformative near term[1]. For a summary and or exploration of implications, skip to "My Take". Introduction > Fool me once. In 1987, Robert Solow quipped, “You can see the computer age everywhere but in the productivity statistics.” Incredibly, this observation happened before the introduction of the commercial Internet and smartphones, and yet it holds to this day. Despite a brief spasm of total factor productivity growth from 1995 to 2005 (arguably due to the economic opening of China, not to digital technology), growth since then has been dismal. In productivity terms, for the United States, the smartphone era has been the most economically stagnant period of the last century. In some European countries, total factor productivity is actually declining. Eli's Thesis In particular, he advances the following sectors as areas AI will fail to revolutionise: * Housing * Most housing challenges are due to land use policy specifically * Housing factors through virtually all sectors of the economy * He points out that the internet did not break up the real estate agent cartel (despite his initial expectations to the contrary) * Energy * Regulatory hurdles to deployment * There are AI optimisation opportunities elsewhere in the energy pipeline, but the regulatory hurdles could bottleneck the economic productivity gains * Transportation * The issues with US transportation infrastructure have little to do with technology and are more regulatory in nature * As for energy, there are optimisation opportunities for digital tools, but the non-digital issues will be the bottleneck * Health * > The biggest gain from AI in medicine would be if it could help us get drugs to market at lower cost. The cost of clinical trials is out of control—up from $10,000 per patient to $500,000
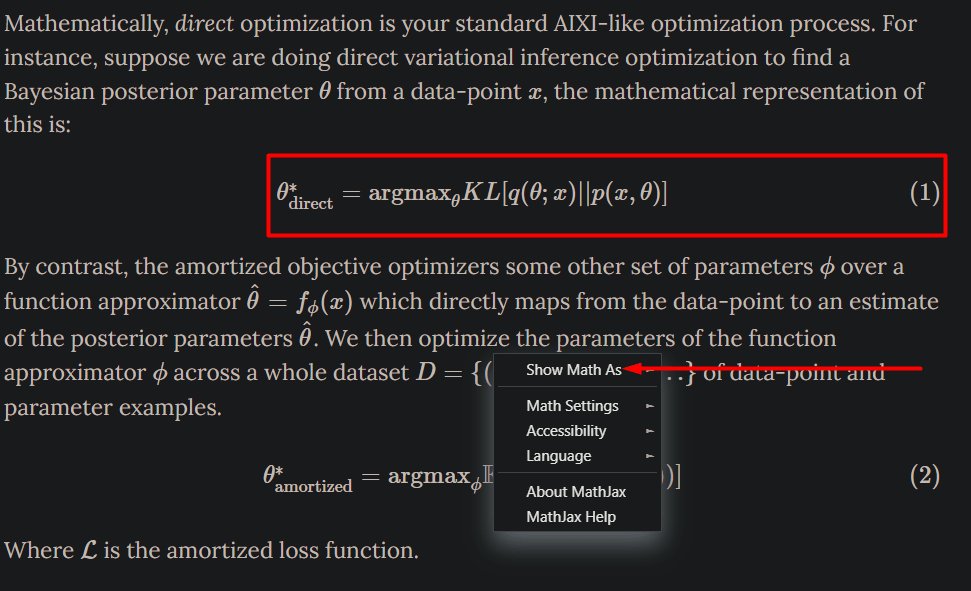

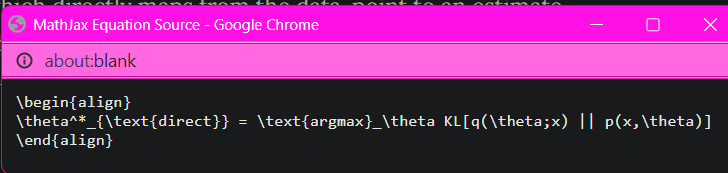


"So8res" is just a stylised "Soares" which is his surname. It's not really a pseudonym in any sense.