Posts
Wiki Contributions
Computing the description length using the entropy of a feature activation's probability distribution is flexible enough to distinguish different types of distributions. For example, a binary distribution would have a entropy of one bit or less, and distributions spread out over more values would have larger entropies.
Yep, that's completely true. Thanks for the reminder!
Really cool stuff! Evaluating SAEs based on the rate-distortion tradeoff is an extremely sensible thing to do, and I hope to see this used in future research.
One minor question/idea: have you considered quantizing different features’ activations differently? For example, one might imagine that some features are only binary (i.e. is the feature on or off) while others’ activations might be used by the model in a fine-grained way. Quantizing different features differently would be a way to exploit this to reduce the entropy. (Of course, performing this optimization and distributing bits between different features seems pretty non-trivial, but maybe a greedy-based approach (e.g. tentatively remove some number of bits from each feature, choose the feature which increases the loss the least, repeat) would work decently enough.)
Another minor question: do the rate-distortion curves of different SAEs intersect? I.e. is it the case that some SAE A achieves a lower loss than SAE B at a low bitrate, but then at a high bitrate, SAE B is better than SAE A? If so, then this might suggest a way to infer hierarchies of features from a set of SAEs: use SAE A to get low-resolution information about your input, and then use SAE B for the high-res detailed information.
Putting these questions aside, this is an area of research that I am extremely interested in, so if you are still working on this or have any new cool results, I would love to see.
Just started playing around with this -- it's super cool! Thank you for making this available (and so fast!) -- I've got a lot of respect for you and Joseph and the Neuronpedia project.
1Do you have any plans of doing something similar for attention layers?
I'm pretty sure that there's at least one other MATS group (unrelated to us) currently working on this, although I'm not certain about any of the details. Hopefully they release their research soon!
Also, do you have any plans to train sparse MLP at multiple layers in parallel, and try to penalise them to have sparsely activating connections between each other in addition to having sparse activations?
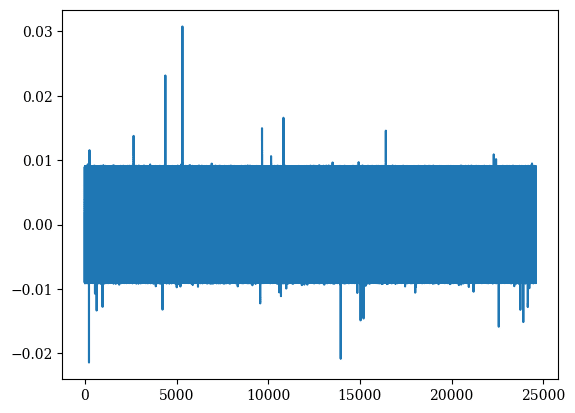
I did try something similar at one point, but it didn't quite work out. In particular: given an SAE for MLP-out activations, you can try and train an MLP transcoder with an additional loss term penalizing the L1 norm of the pullback of the SAE encoder features by the transcoder decoder matrix. This was intended to induce sparse input-independent connections from the transcoder features to the MLP-out SAE features. Unfortunately, this didn't yield great results. The transcoder features were often polysemantic, while the input-independent connections from the transcoder features to the SAE features were somewhat bizarre-looking. Here's an old graph I just dug up: the x-axis is transcoder feature index and the y-axis is the input-independent connection strength to a certain SAE feature:
In the end, I decided to pause working on this idea. Potentially, it could turn out that this idea is workable, but if so, then there are probably a few extra tweaks that have to be done to get it working beyond the naive approach that I tried.
This seems reasonable enough to me. For what it's worth, the other main reason why I'm particularly interested in whether different SAEs' rate-distortion curves intersect is because if this is the case, then comparing two SAEs becomes more difficult: depending on the bitrate that you're evaluating at, SAE A might be better than SAE B or vice versa. On the other hand, if SAE A's rate-distortion curve is always above SAE B, then it means that the answer to "which SAE is better?" doesn't depend on any hyperparameter (bitrate, or conversely, acceptable loss threshold). I imagine that the former case is probably true, in which case heuristics for acceptable loss thresholds or reasonable bitrates will probably be developed. But it'd be really nice if the latter case turned out to be true, so I'm personally curious to see whether it is.