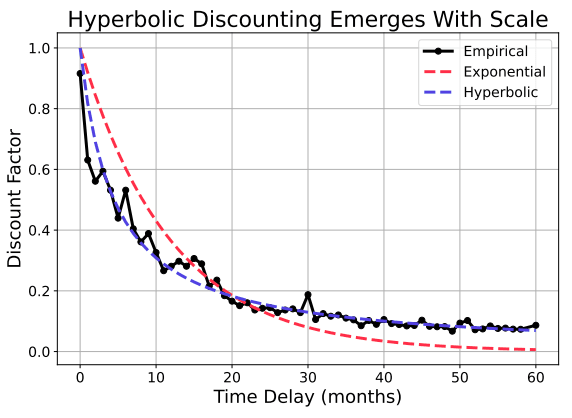
Loss Curves
Or, why GAN training looks so funky. Solomonoff's Lightsaber > The simplest explanation is exponentially more important. Suppose I give you a pattern, and ask you to explain what is going on: 1,2,4,8,16,… Several explanations might come to mind: * "The powers of two," * "Moser's circle problem," * x424−x312+11x224+7x12+1, * "The counting numbers in an alien script," * "Fine-structure constants." Some of these explanations are better than others, but they could all be the "correct" one. Rather than taking one underlying truth, we should assign a weight to each explanation, with the ones more likely to produce the pattern we see getting a heavier weight: Grand Unified Explanation=∑wexplanation⋅explanation. Now, what exactly is meant by the word "explanation"? Between humans, our explanations are usually verbal signals or written symbols, with a brain to interpret the meaning. If we want more precision, we can program an explanation into a computer, e.g. fn pattern(n) {2^n}. If we are training a neural network, an explanation describes what region of weight-space produces the pattern we're looking for, with a few error-correction bits since the neural network is imperfect. See, for example, the paper "ARC-AGI Without Pretraining" (Liao & Gu). Let's take the view that explanations are simply a string of bits, and our interpreter does the rest of the work to turn it into words, programs, or neural networks. This means there are exactly 2n n-bit explanations, and the average weight for each of them is less than 1/2n. Now, most explanations—even the short ones—have hardly any weight, but there are still exponentially more longer explanations that are "good"[1]. This means, if we take the most prominent n explanations, we would expect the remaining explanations to have weight on the order of exp(−n). Counting Explanations > What you can count, you can measure. Suppose we are training a neural network, and we want to count how many explanations it has learned
