Marco Discendenti

Boltzmann brain's conditional probability

Can we estimate the probability of this 3rd hypothesis or even compare it with the probability of the other two?

Boltzmann brain's conditional probability

Boltzmann conjectured that the low entropy universe we live in could be the result of a very big fluctuation in entropy in a universe that stays most of the time in thermodynamic equilibrium. This scenario is called "Boltzmann universe". Some have argued that if this were the case then, with a high probability, we should not be really living in the universe that we "see", we are more likely to be just a single isolated brain experiencing an illusionary ordered universe that is not real. This is because this last event seems less improbable than the formation of the entire low entropic world that we think are experiencing. This lonely brain scenario... (read 843 more words →)

Marco Discendenti2y*

Itt seems to me that it is actually easy to define a function $u'(...)>=0$ such that the preferences are represented by $E(u'^2)$ and not by $E(u')$: just take u'=sqrt(u), and you can do the same for any value of the exponent, so the expectation does not play a special role in the theorem, you can replace it with any $L^p$ norm.

-1

Marco Discendenti2y*

There are infinitely many ways to find utility functions that represents preferences on outcomes, for example if outcomes are monetary than any increasing function is equivalent on outcomes but not when you try to extend it to distributions and lotteries with the expected value.
I wander if given a specific function u(...) on every outcome you can also chose "rational" preferences (as in the theorem) according to some other operator on the distributions that is not the average, for example what about the L^p norm or the sup of the distribution (if they are continuous)?
Or is the expected value the special unique operator that have the propety stated by the VN-M theorem?

-1

You don't necessarily need to start from the preference and use the theorem to define the function, you can also start from the utility function and try to produce an intuitive explanation of why you should prefer to have the best expected value

Thank you for your insight. The problem with this view of utility "just as a language" is that sometimes I feel that the conclusion of utility maximization are not "rational" and I cannot figure out why they should be indeed rational if the language is not saying anything that is meaningful to my intuition.

Marco Discendenti2y*

Very interesting observations. I woudln't say the theorem is used to support his assumption because the assumptions don't speak about utils but only about preference over possible outcomes and lotteries, but I see your point.

Actually the assumptions are implicitly saying that you are not rational if you don't want to risk to get a 1'000'000'000'000$ debt with a small enough probability rather than losing 1 cent (this is strightforward from the archimedean property).

Ok we have a theorem that says that if we are not maximizing the expected value of some function "u" then our preference are apparently "irrational" (violating some of the axioms). But assume we already know our utility function before applying the theorem, is there an argument that shows how and why the preference of B over A (or maybe indifference) is irrational if E(U(A))>E(U(B))?

Apparently the axioms can be considered to talk about preferences, not necessarily about probabilistic expectations. Am I wrong in seeing them in this way?

It seems indeed quite reasonable to maximize utility if you can choose an option that makes it possible, my point is why you should maximize expected utility when the choice is under uncertainty

How could humans dominate over a super intelligent AI?

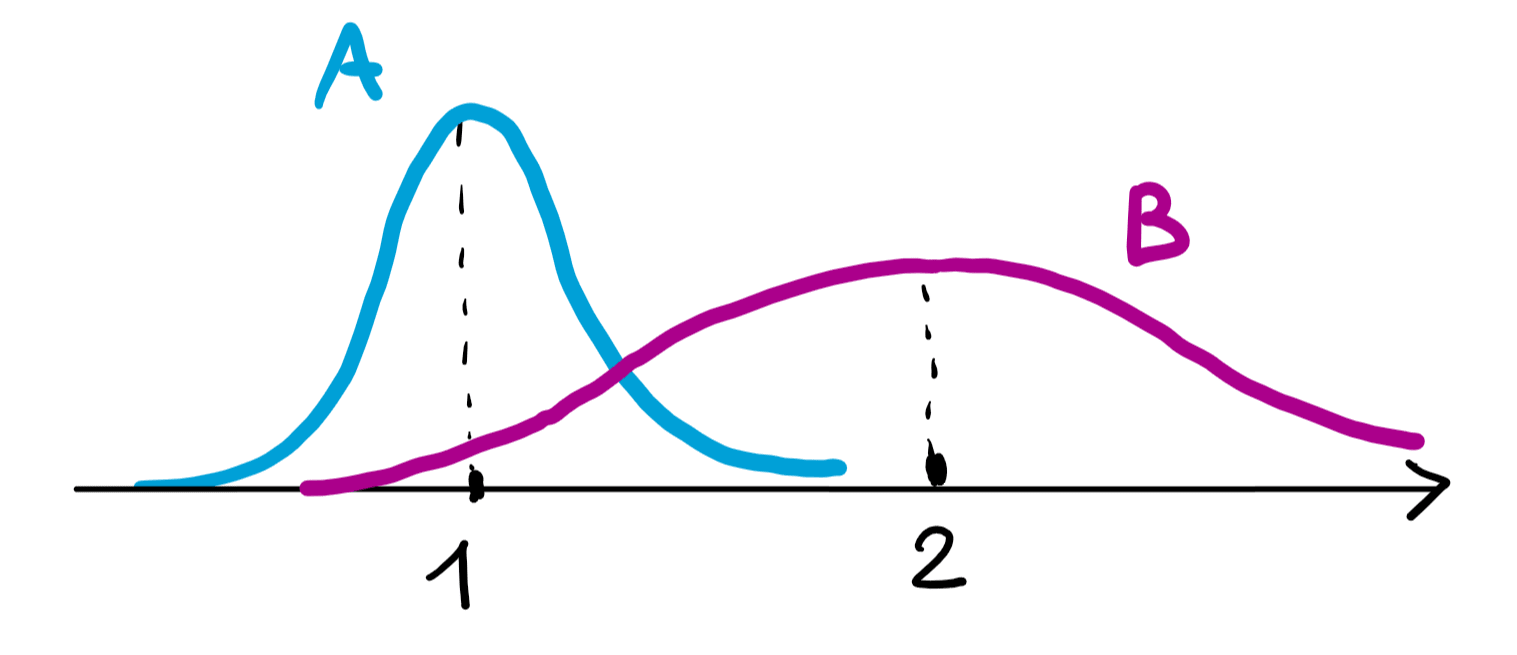
In the context of decision making under uncertainty we consider the strategy of maximizing the expected monetary revenue and expected utility; we provide an argument to show that under certain hypothesis it is rational to maximize expected monetary revenue, then we show that the argument doesn't apply to expected utility. We are left with the question about how do we justify the rationality of the strategy of maximizing expected utility.

Expected monetary revenue

Suppose you have to choose one of two games A and B with an expected economic return of 1$ and 2$ respectively, which have a certain probability distribution.

If you play many times, say N, the law of large numbers and the central... (read 1121 more words →)

Unconvenient consequences of the logic behind the second law of thermodynamics

Imagine a future where:

more and more powerful AIs are created by humans;
they can mimic human intellectual abilities and make speculations like super geniuses;
they are used to work at scientific and technologic research and they produce theories and technologies that no human is intelligent enough to understand;
humans become dependent on this advanced science and technology and they need AIs to work at it.

My question is: in this scenario is there a way for humans to keep their dominion over these AIs? Could they possibly embed these AIs with a submissive "personality"? Would this be enough to avoid that they will use their superior understanding of reality to manipulate humans even while being submissive and obidient?

-5

Expected utility and repeated choices

Let's consider a simple universe consisting of an ideal gas inside a box (which means a number of massive points behaving as prescribed by Newton's physics with completely elastic collisions).

After the system reaches the thermodynamic equilibrium you could ask if it will stay forever in this equilibrium state, the answer turns out to be negative: Poincarè recurrence Theorem applies and we can be sure that the system will go far from equilibrium again and again given a sufficiently long "life" for this universe. Therefore entropy in this universe will be a fluctuating function like this:

If you are patient enough you would see

countinuous micro-fluctuations
occasional slightly bigger fluctuations
rare "not-so-small" fluctioations
extremely rare medium-big fluctuation
unconceiveably rare

... (read 507 more words →)