It sounds like you're assuming you have access to some "true" probability for each event; do I misunderstand? How would I determine the "true" probability of e.g. Harris winning the 2028 US presidency? Is it 0/1 depending on the ultimate outcome?

(Hmm. Come to think of it, if the y-axis were in logits, the error bars might be ill-defined, since "all the predictions come true" would correspond to +inf logits.)

Ah-- I took every prediction with p<0.50 and flipped 'em, so that every prediction had p>=0.50, since I liked the suggestion "to represent the symmetry of predicting likely things will happen vs unlikely things won't."

Thanks for the close attention!

I like the idea, but with n>100 points a histogram seems better, and for few points it's hard to draw conclusions. e.g., I can't work out an interpretation of the stdev lines that I find helpful.

Nyeeeh, I see your point. I'm a sucker for mathematical elegance, and maybe in this case the emphasis is on "sucker."

I'd make the starting point p=0.5, and use logits for the x-axis; that's a more natural representation of probability to me. Optionally reflect p<0.5 about the y-axis to represent the symmetry of predicting likely things will happen vs unlikely things won't.

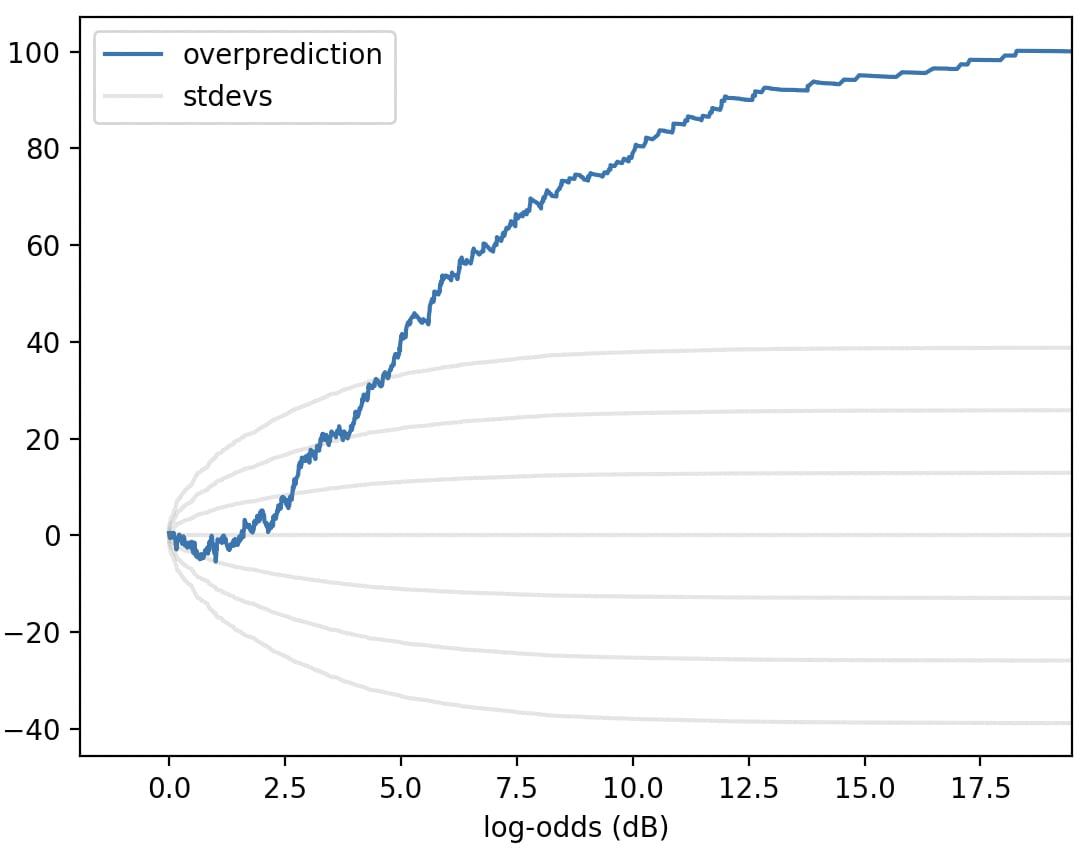
(same predictions from my last graph, but reflected, and logitified)

Hmm. This unflattering illuminates a deficiency of the "cumsum(prob - actual)" plot: in this plot, most of the rise happens in the 2-7dB range, not because that's where the predictor is most overconfident, but because that's where most of the predictions are. A problem that a normal calibration plot wouldn't share!

(A somewhat sloppy normal calibration plot for those predictions:

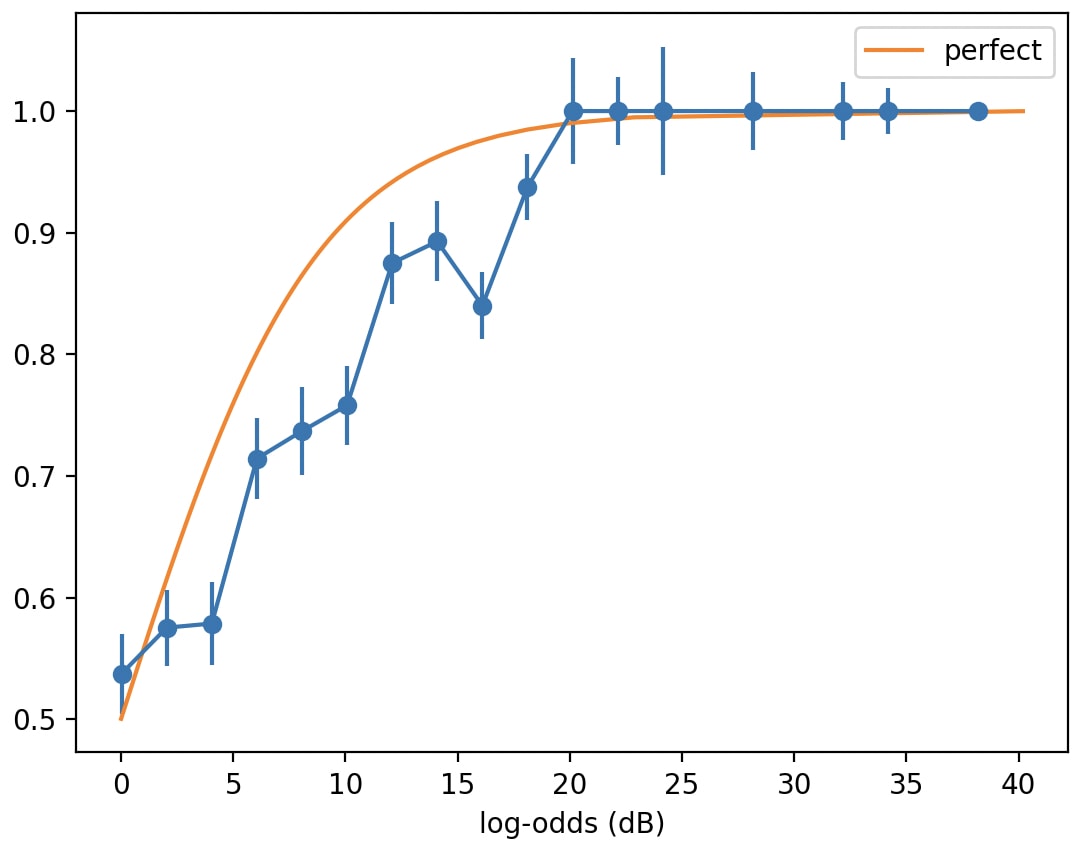
Perhaps the y-axis should be be in logits too; but I wasn't willing to figure out how to twiddle the error bars and deal with buckets where all/none of the predictions came true.)

Random numbers! Code for the last figures.

That all of physics was perfectly beautiful and symmetric except for hyperspace, artificial gravity, shields and a few weapon types.

Oh, this is genius. I love this.

Ahhh! Yes, this is very helpful! Thanks for the explanation.

Question: if I'm considering an isolated system (~= "the entire universe"), you say that I can swap between state-vector-format and matrix-format via

. But later, you say...

If $H_S$ is uncoupled to its environment (e.g. we are studying a carefully vacuum-isolated system), then we still have to replace the old state vector picture $|\varphi ⟩\in H$ by a (possibly rank $>1$) density matrix $\rho \in {\text{Op}}_H$...

But if $\rho :=|\varphi ⟩⟨\varphi |$, how could it ever be rank>1?

(Perhaps more generally: what does it mean when a state is represented as a rank>1 density matrix? Or: given that the space of possible $\rho$s is much larger than the space of possible $|\varphi ⟩$s, there are sometimes (always?) multiple $\rho$s that correspond to some particular $|\varphi ⟩$; what's the significance of choosing one versus another to represent your system's state?)

That is... a very interesting and attractive way of looking at it. I'll chew on your longer post and respond there!

I have an Anki deck in which I've half-heartedly accumulated important quantities. Here are mine! (I keep them all as log10(value in kilogram/meter/second/dollar/whatever seems natural), to make multiplication easy.)