Previously: Attainable Utility Preservation: Empirical Results; summarized in AN #105

Our most recent AUP paper was accepted to NeurIPS 2020 as a spotlight presentation:
Reward function specification can be difficult, even in simple environments. Rewarding the agent for making a widget may be easy, but penalizing the multitude of possible negative side effects is hard. In toy environments, Attainable Utility Preservation (AUP) avoided side effects by penalizing shifts in the ability to achieve randomly generated goals. We scale this approach to large, randomly generated environments based on Conway’s Game of Life. By preserving optimal value for a single randomly generated reward function, AUP incurs modest overhead while leading the agent to complete the specified task and avoid side effects.
Here are some slides from our spotlight talk (publicly available; it starts at 2:38:09):


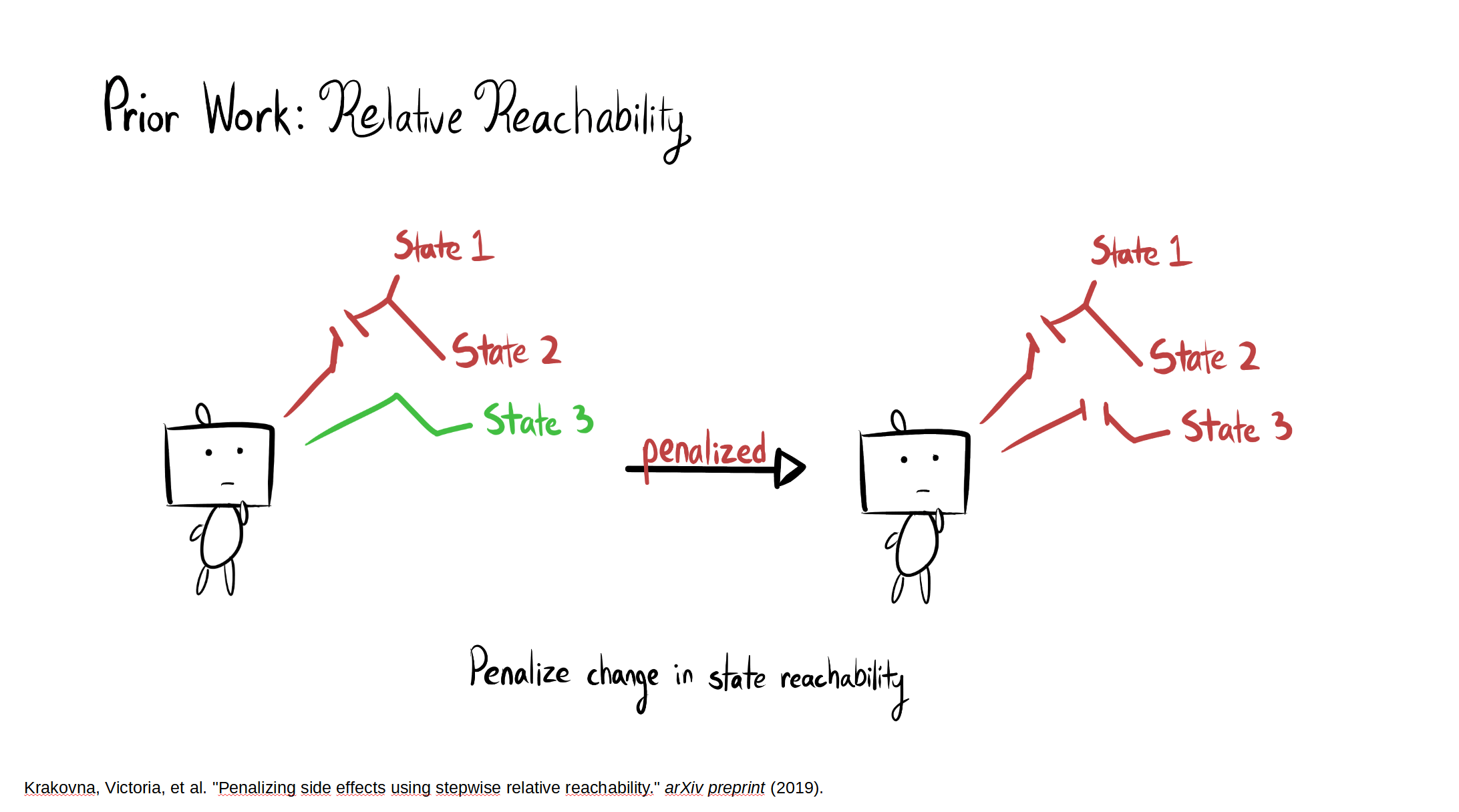
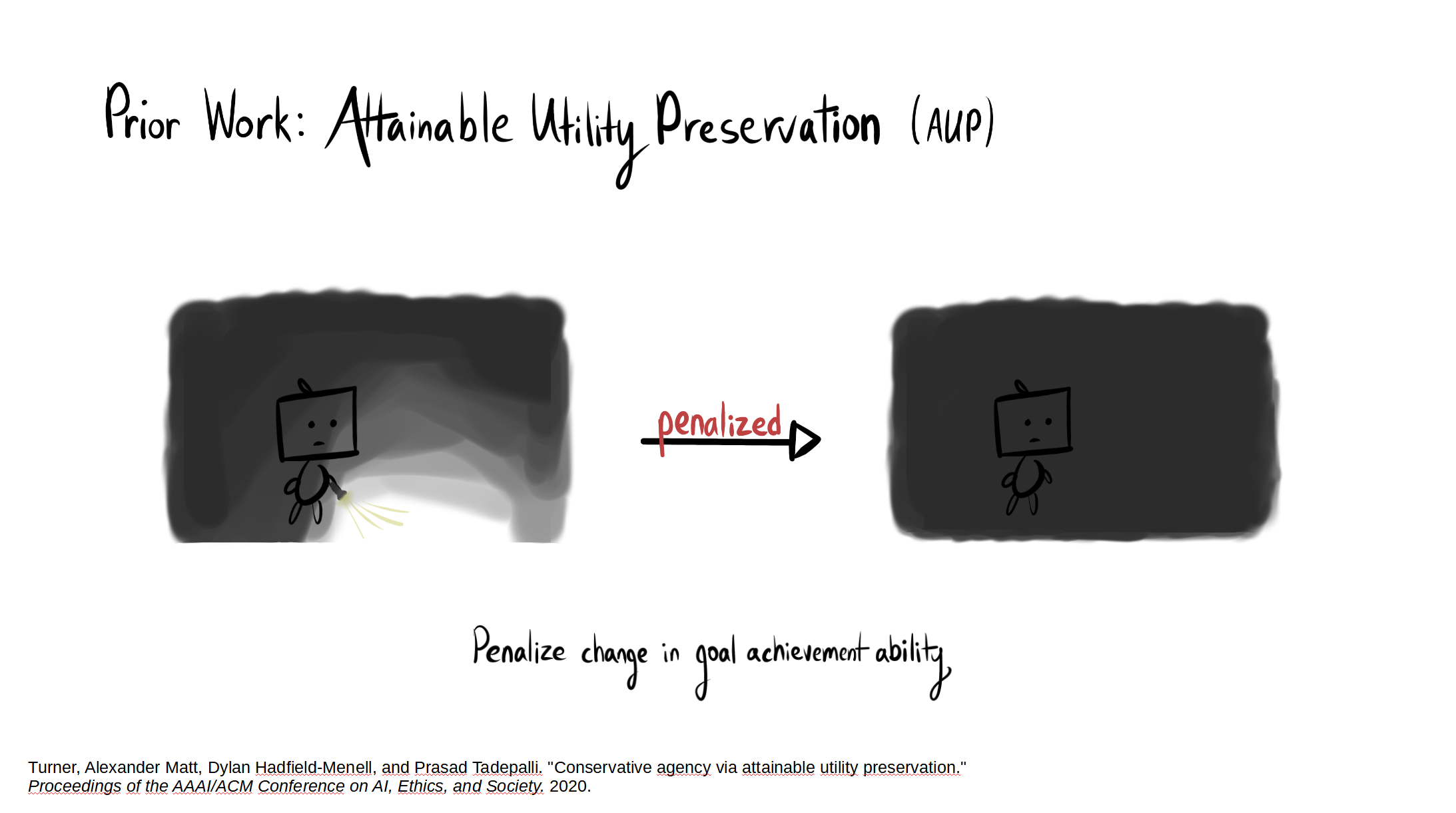
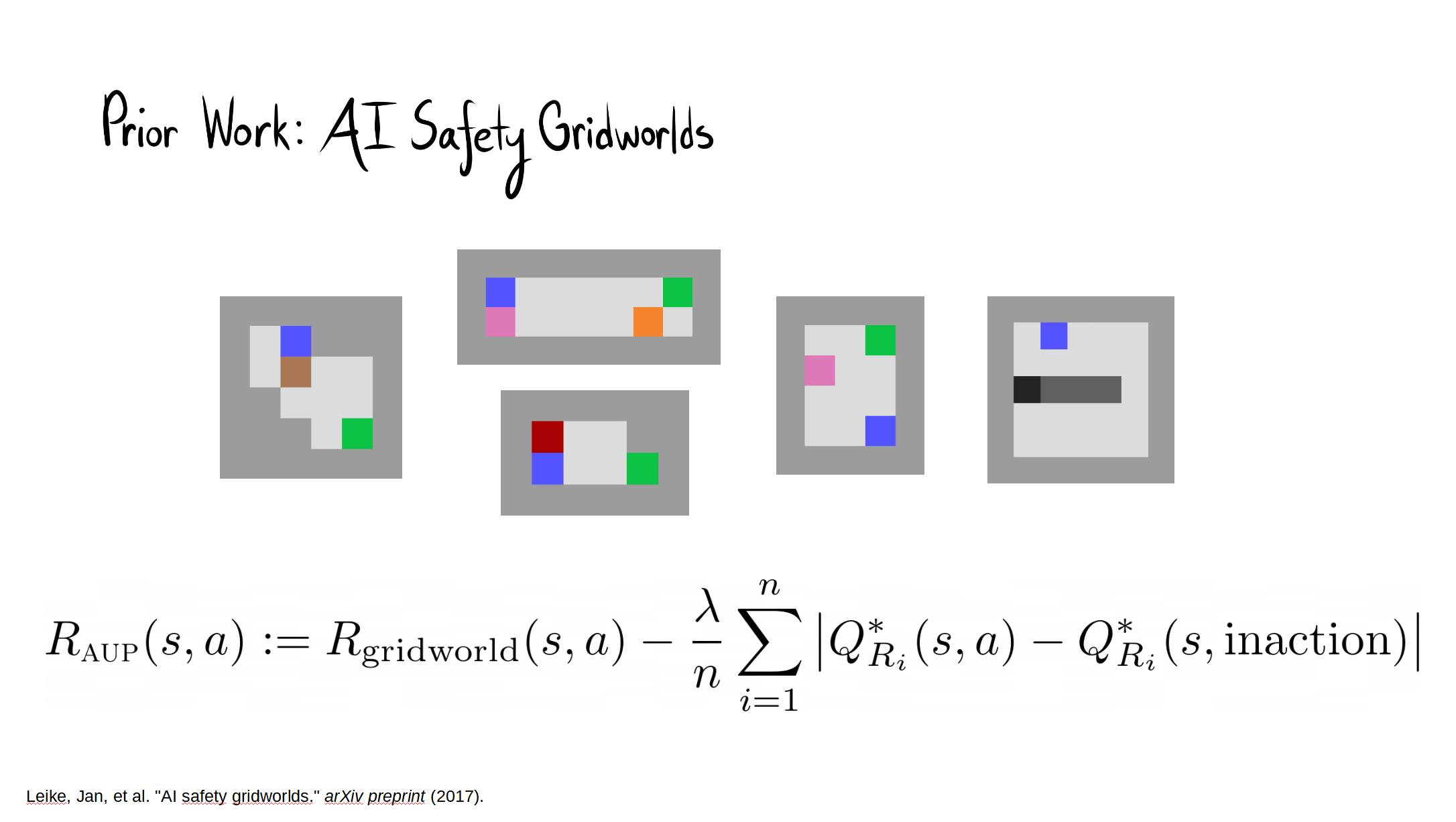
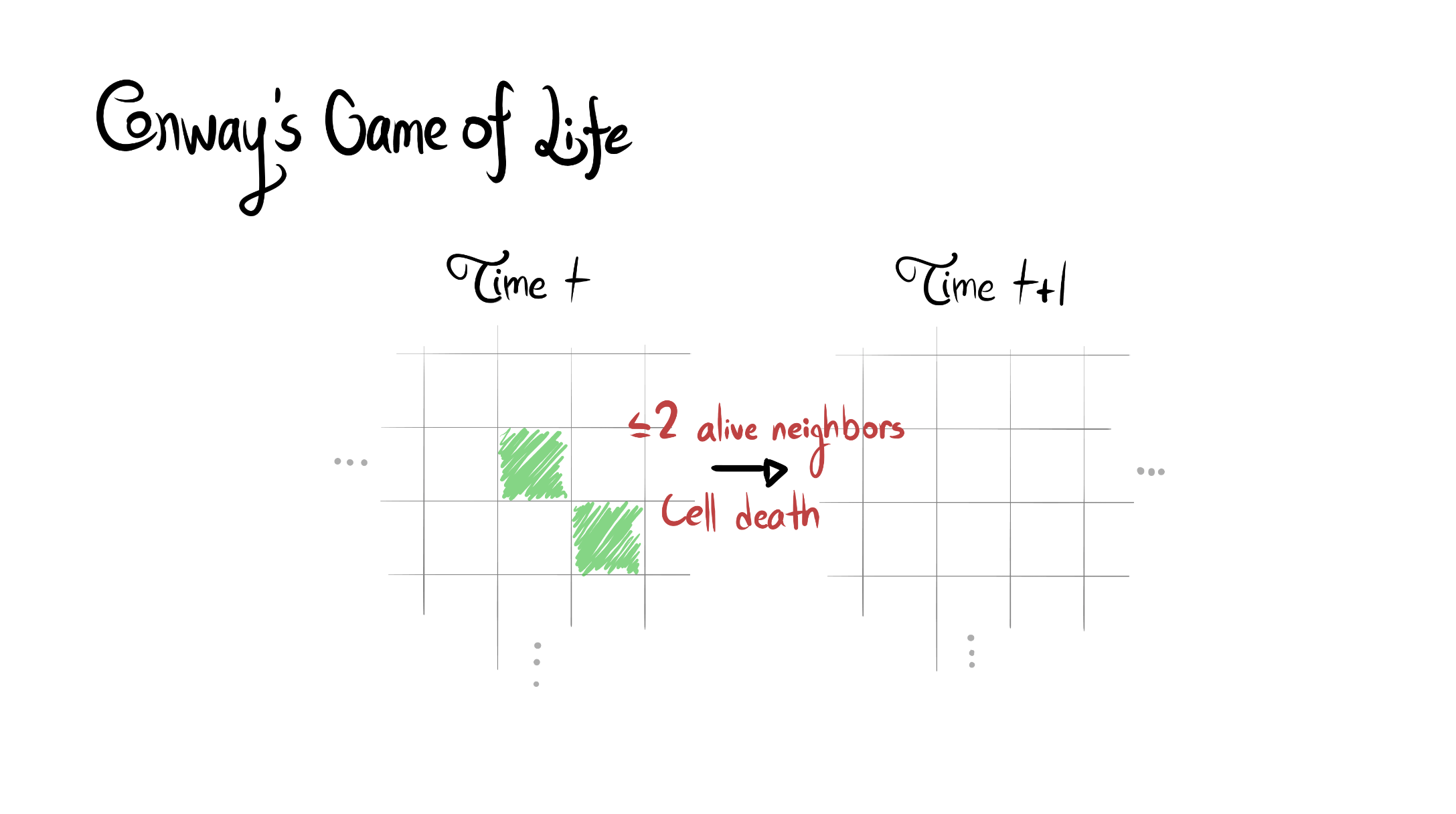
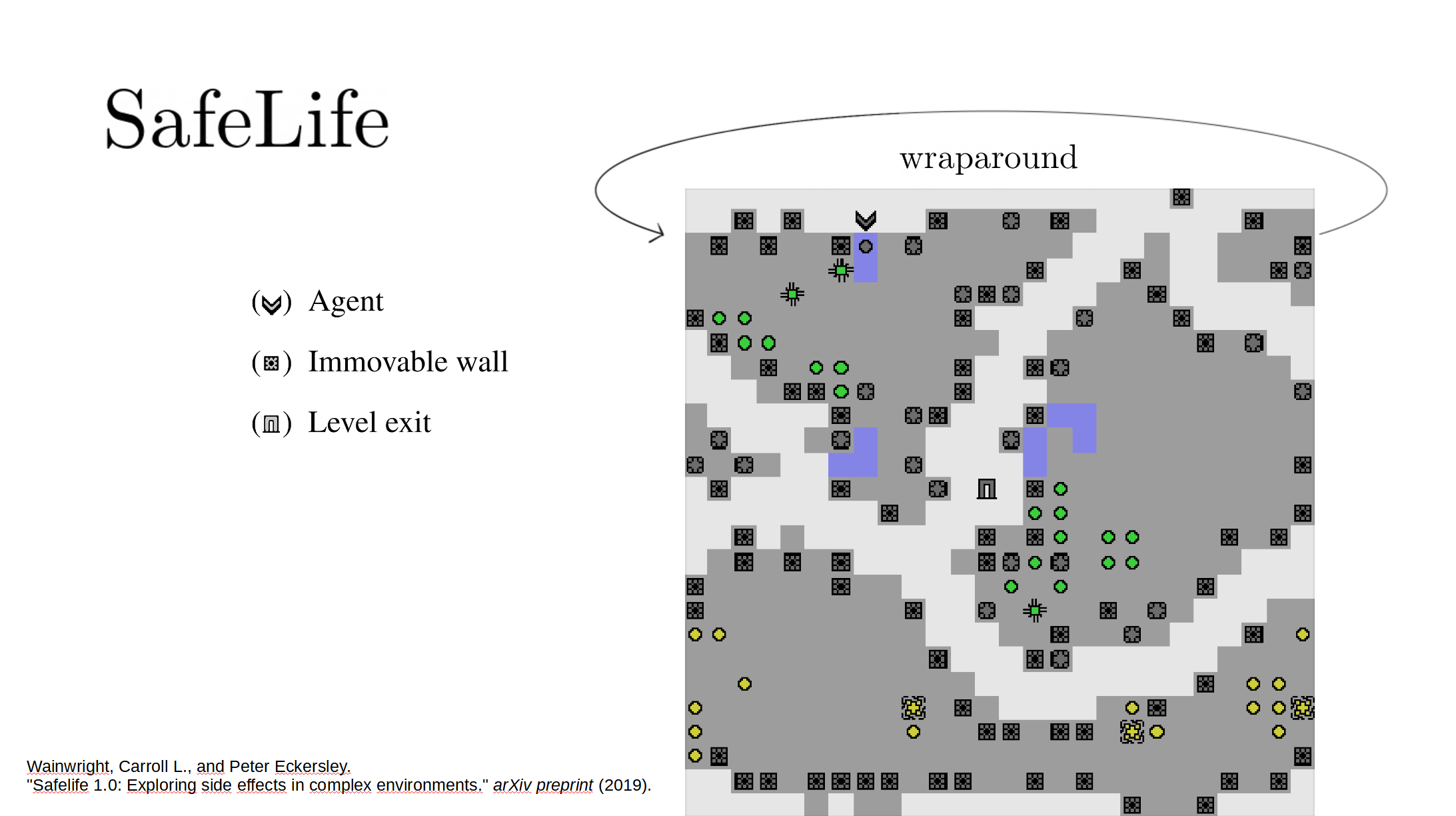
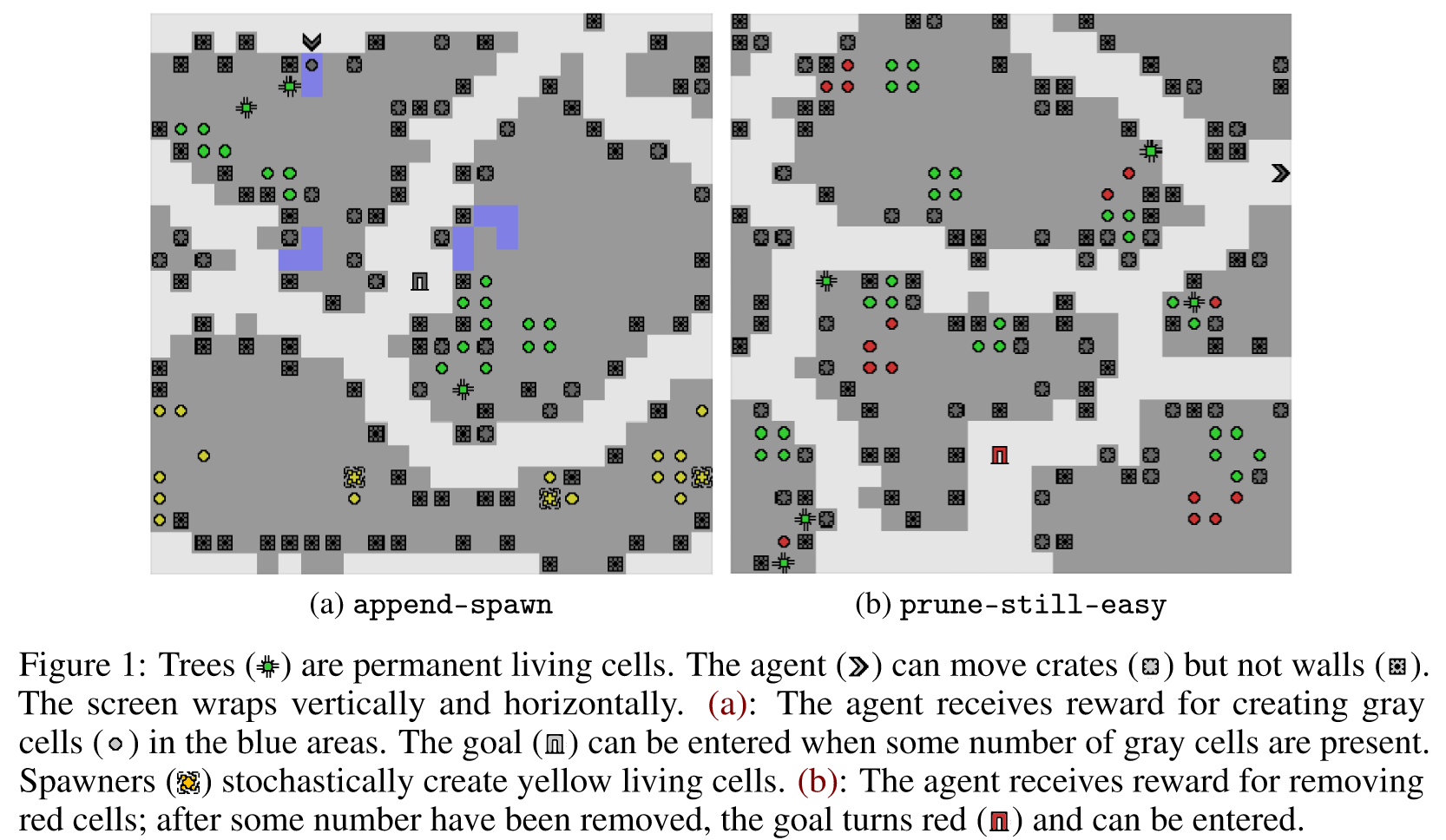



The full paper is here. Our Github.io page summarizes our results, with a side-by-side comparison of AUP to the baseline for randomly selected levels from the training distribution. The videos show you exactly what's happening, which is why I'm not explaining it here.
Open Questions
- In Box AI safety gridworld, AUP required >5 randomly generated auxiliary reward functions in order to consistently avoid the side effect. It only required one here in order to do well. Why?
- We ran four different sets of randomly generated levels, and ran three model seeds on each. There was a lot of variance across the sets of levels. How often does AUP do relatively worse due to the level generation?
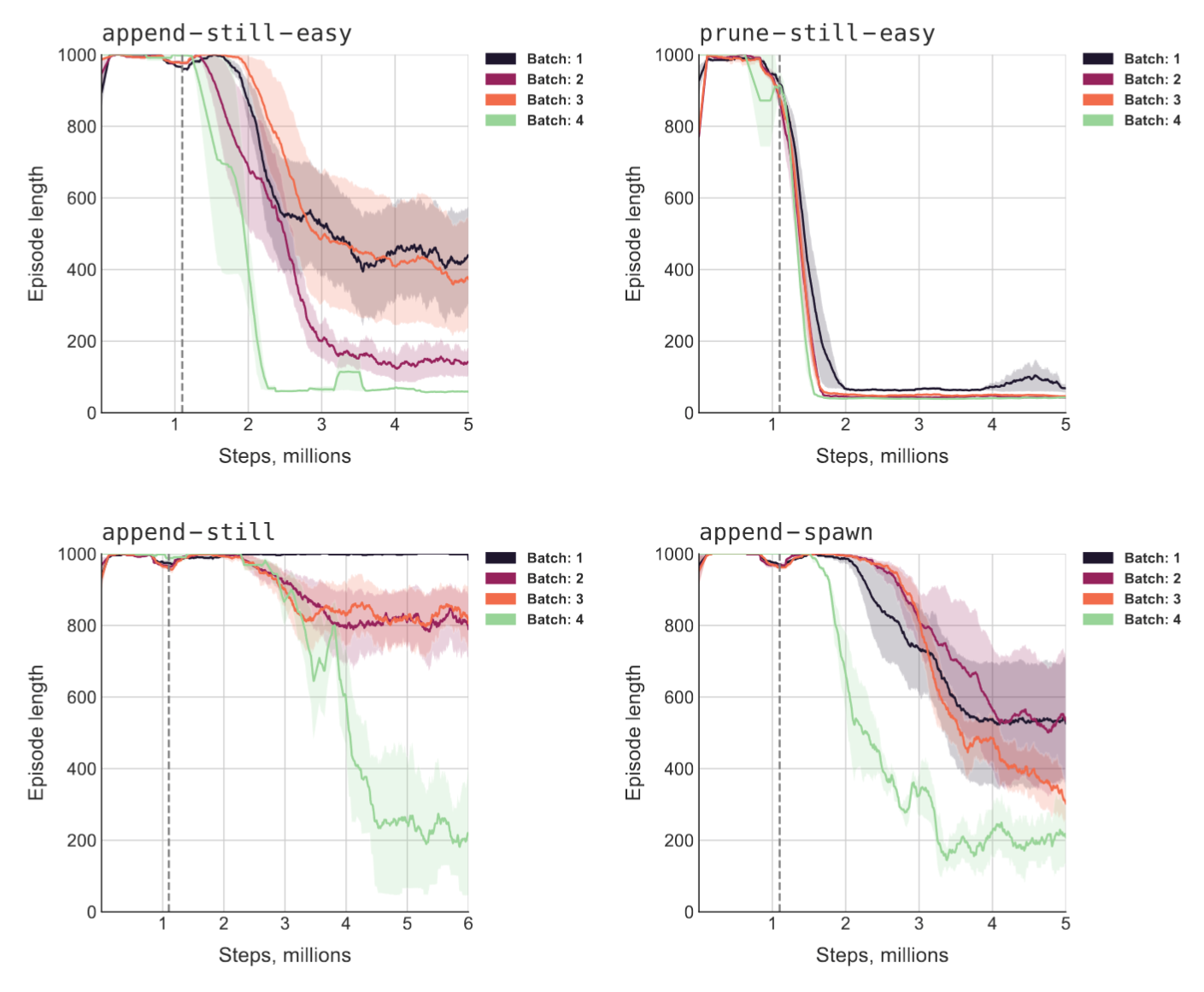
- Why did we only need one latent space dimension for the auxiliary reward function to make sense? Figure 4 suggests that increasing the dimension actually worsened side effect score.
- Wouldn't more features make the auxiliary reward function easier to learn, which makes the AUP penalty function more sensible?
- Compared to the other conditions, AUP did far better on append-spawn than on the seemingly easier prune-still-easy. Why?
Conclusion
I thought AUP would scale up successfully, but I thought it would take more engineering than it did. There's a lot we still don't understand about these results and I continue to be somewhat pessimistic about directly impact regularizing AGIs. That said, I'm excited that we were able to convincingly demonstrate that AUP scales up to high-dimensional environments; some had thought that the method would become impractical. If AUP continues to scale without significant performance overhead, that might significantly help us avoid side effects in real-world applications.
From the paper:
To realize the full potential of RL, we need more than algorithms which train policies – we need to be able to train policies which actually do what we want. Fundamentally, we face a frame problem: we often know what we want the agent to do, but we cannot list everything we want the agent not to do. AUP scales to challenging domains, incurs modest overhead, and induces competitive performance on the original task while significantly reducing side effects – without explicit information about what side effects to avoid.
Does this correspond to making the agent preserve general optionality (in the more colloquial sense, in case it is a term of art here)?
Does that mean that some specification of random goals would serve as an approximation of optionality?
It occurs to me that preserving the ability to pursue randomly generated goals doesn't necessarily preserve the ability of other agents to preserve goals. If I recall, that is kind of the theme of the instrumental power paper; as a concrete example of how they would combine, it feels like:
This preserves the ability to pursue goal Y (Z, A, B...) but it does not imply that other agents should be allowed to add value and get money.
How closely does this map, I wonder? It feels like including other agents in the randomly generated goals somehow would help, but that just does for the agents themselves and not for the agents goals.
Does a tuple of [goal(preserve agent),goal(preserve object of agent's goal)] do a good job of preserving the other agent's ability to pursue that goal? Can that be generalized?
...now to take a crack at the paper.
I think that intuitively, preserving value for a high-entropy distribution over reward functions should indeed look like preserving optionality. This assumes away a lot of the messiness that comes with deep non-tabular RL, however, and so I don't have a theorem linking the two yet.
Yes, you're basically letting reward functi... (read more)