Found in an old Kahneman & Tversky paper:
There are two programs in a high school. Boys are a majority (65%) in program A, and a minority (45%) in program B. There is an equal number of classes in each of the two programs.
You enter a class at random, and observe that 55% of the students are boys. What is your best guess -- does the class belong to program A or to program B?
Oops, you're right. The variant of the problem I mentioned above got rid of the assumption of binomially distributed boys (equivalently, girls).
The following setup should work, though:
In words, this says that to generate the i-th class, you flip a coin to tell whether it's in program A or program B, conditioned on the program, the proportion of boys is drawn from a program-specific beta distribution, and then the number of boys is drawn from the corresponding binomial distribution. Under the constraints that %20=%200.65) and
%20=%200.65) and  %20=%200.45), the average proportion of boys matches up with the problem.
%20=%200.45), the average proportion of boys matches up with the problem.
However, by taking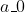 or
or 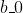 small (where
small (where 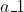 and
and 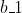 are adjusted accordingly to maintain the constraint), you can play with the variance so that the observed 55% boys class is more likely under either of the programs. If you had available repeated trials, you might be able to learn
are adjusted accordingly to maintain the constraint), you can play with the variance so that the observed 55% boys class is more likely under either of the programs. If you had available repeated trials, you might be able to learn 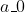 and
and 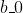 . In a single trial, you can't be sure that your strategy will do worse than chance.
. In a single trial, you can't be sure that your strategy will do worse than chance.