People seem to be continually surprised, over and over again, by the new capabilities of big machine learning models, such as PaLM, DALL-E, Chinchilla, SayCan, Socratic Models, Flamingo, and Gato (all in the last two months!). Luckily, there is a famous paper on how AI progress is governed by scaling laws, where models predictably get better as they get larger. Could we forecast AI progress ahead of time by seeing how each task gets better with model size, draw out the curve, and calculate which size model is needed to reach human performance?
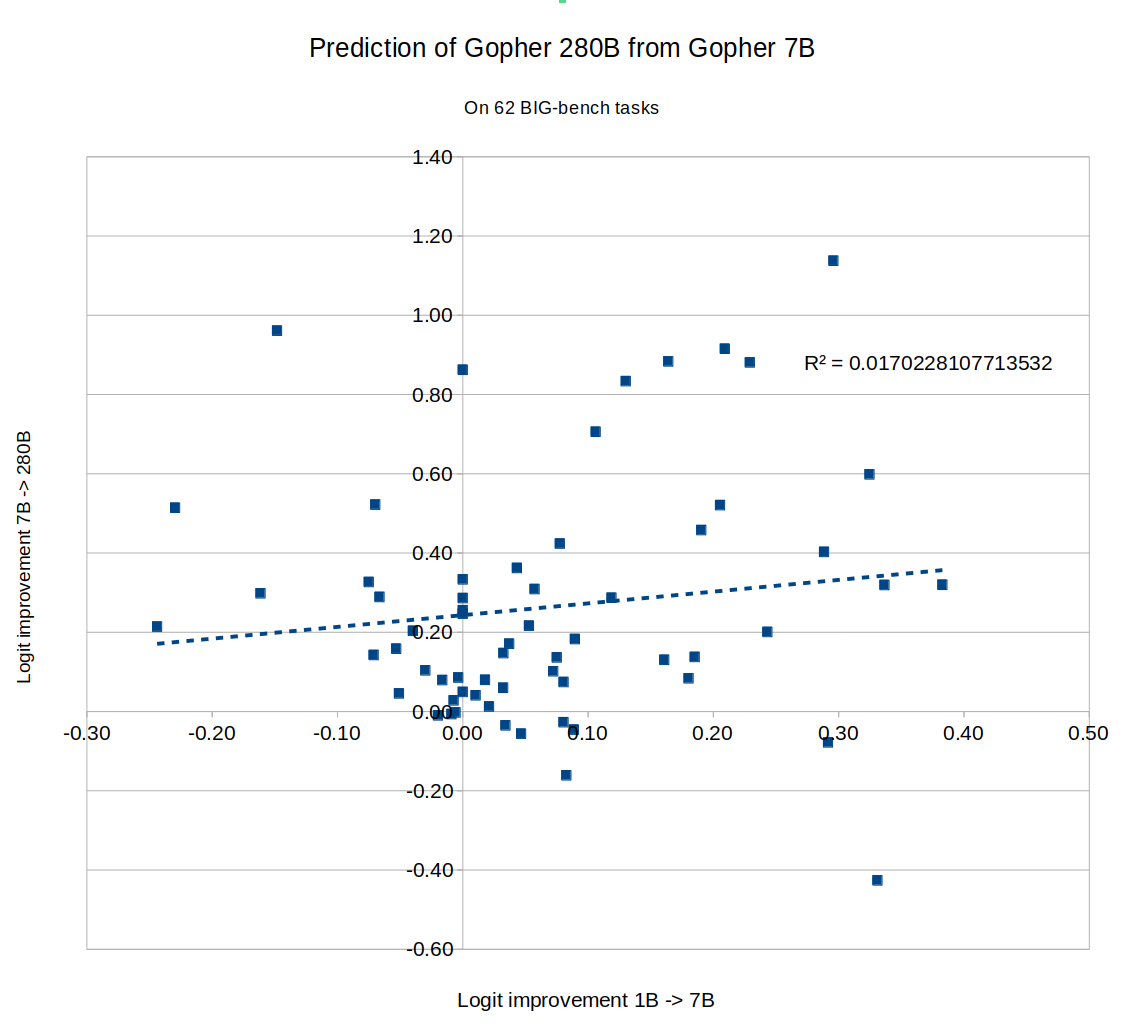
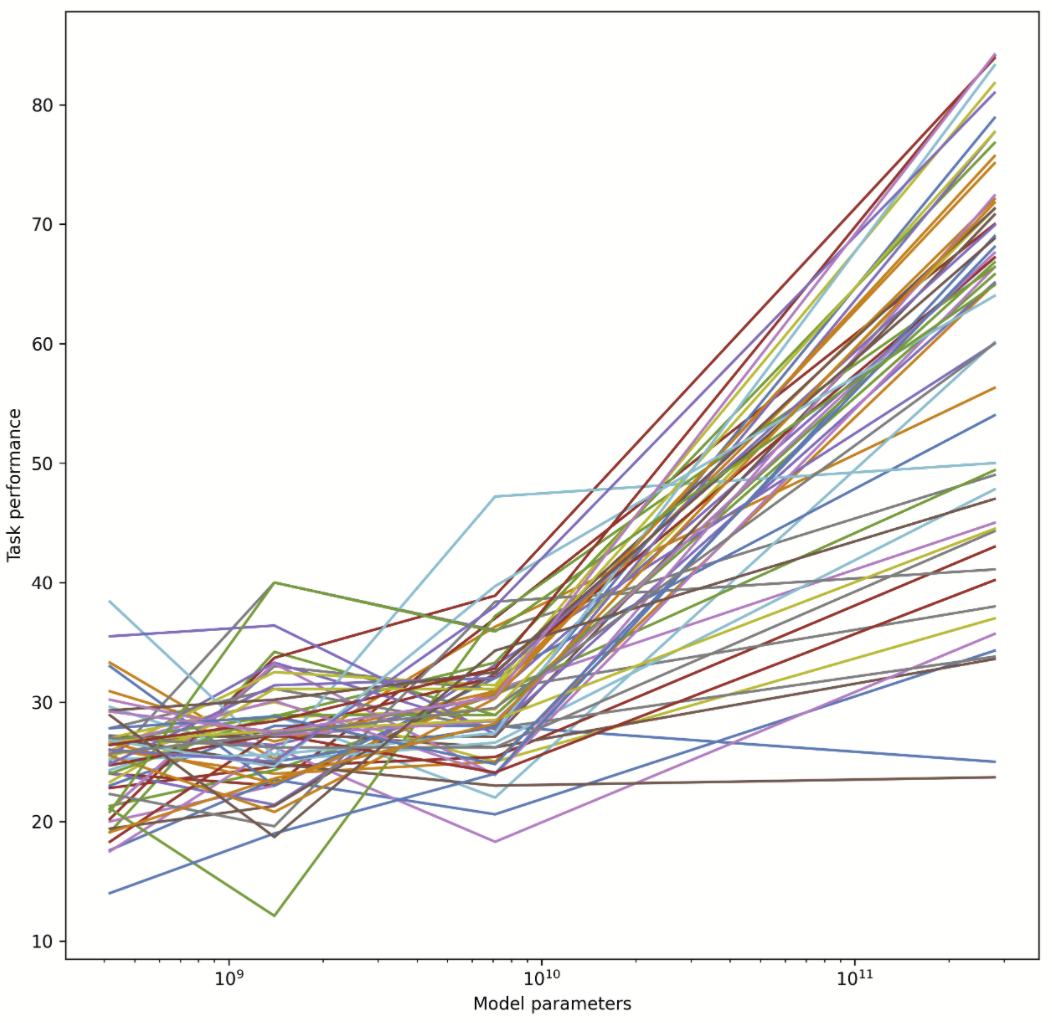
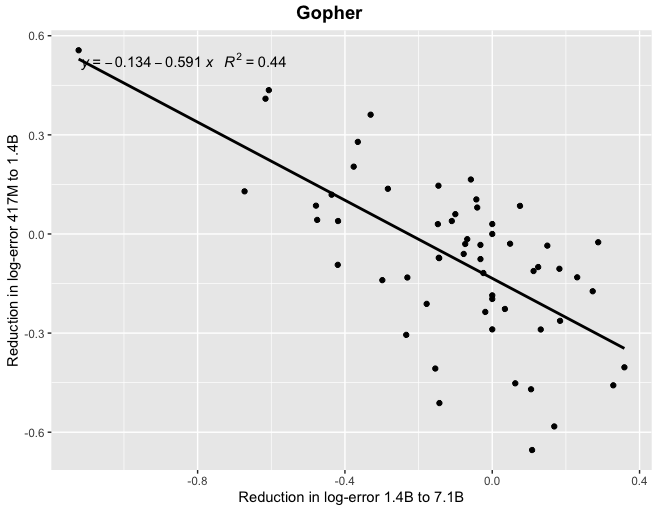
I tried this, and apparently the answer is no. In fact, whether AI has improved on a task recently gives us exactly zero predictive power for how much the next model will improve on the same task. The sheer consistency of this unpredictability is remarkable, almost like a law of statistical thermodynamics. No matter what I plug in, the correlation is always zero! For example, does a task improving rapidly when you go from a small model to a 7B parameter model predict similar improvement when you go from a 7B model to Gopher's 280B? No:
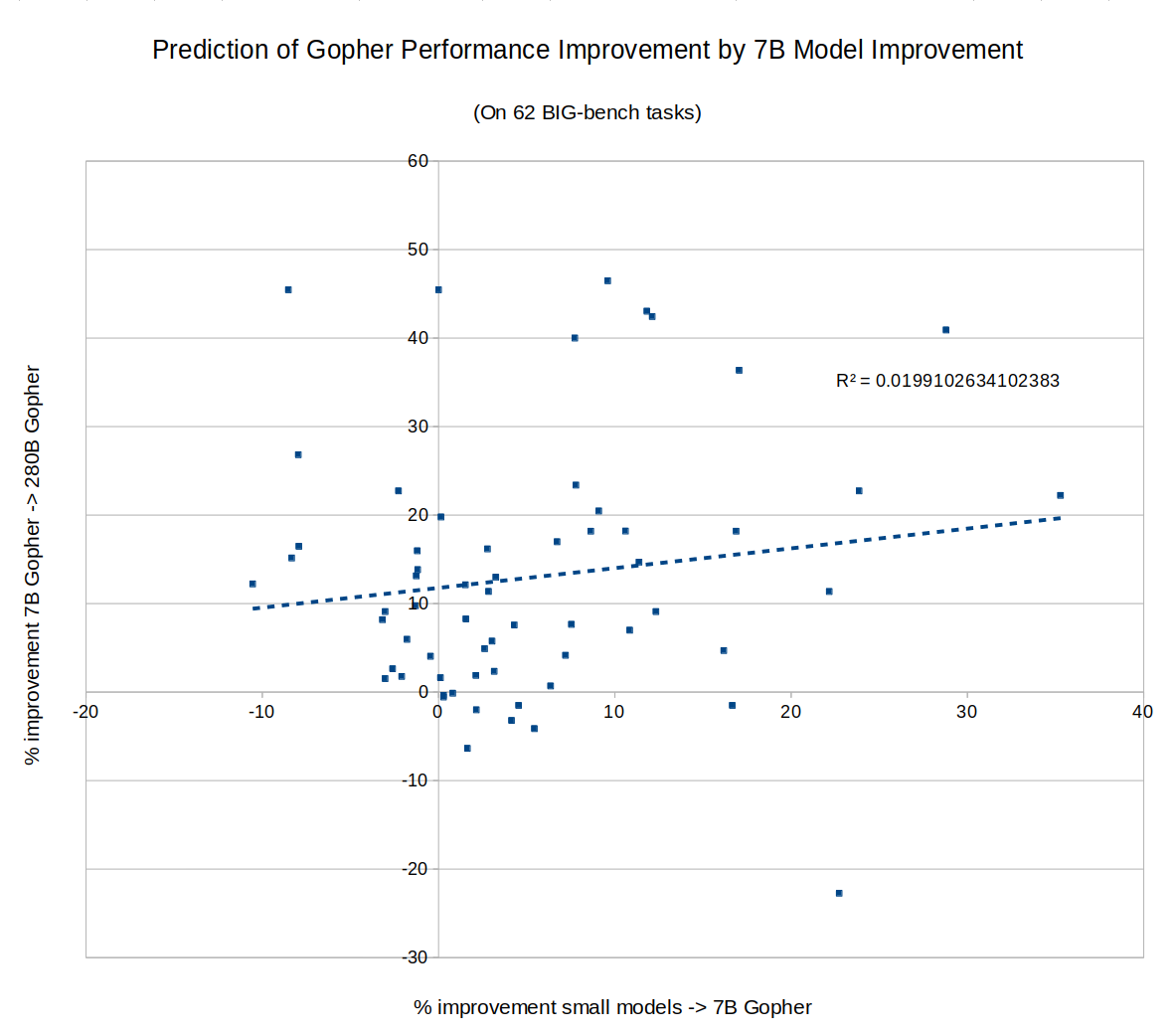
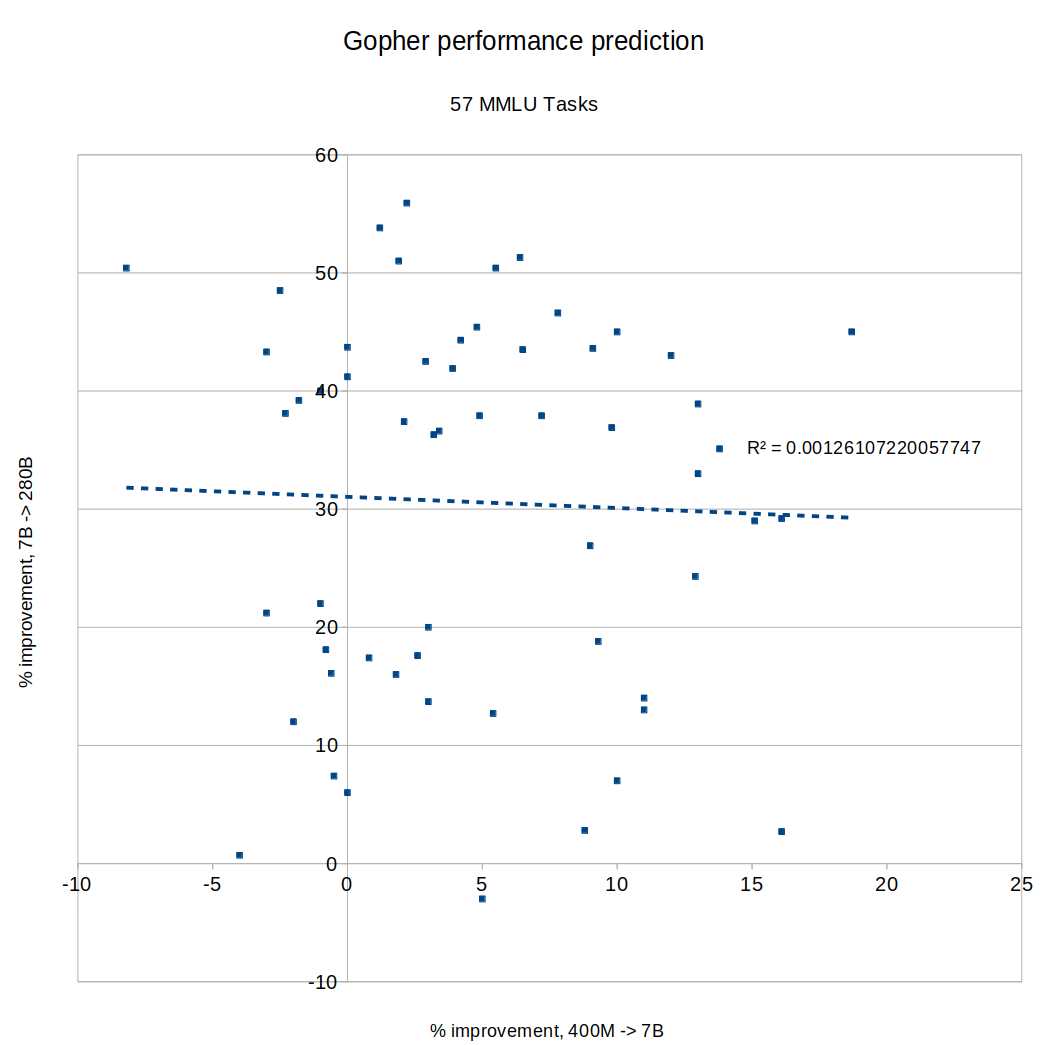
I tried making the same graph with MMLU tasks instead of BIG-bench, same result:
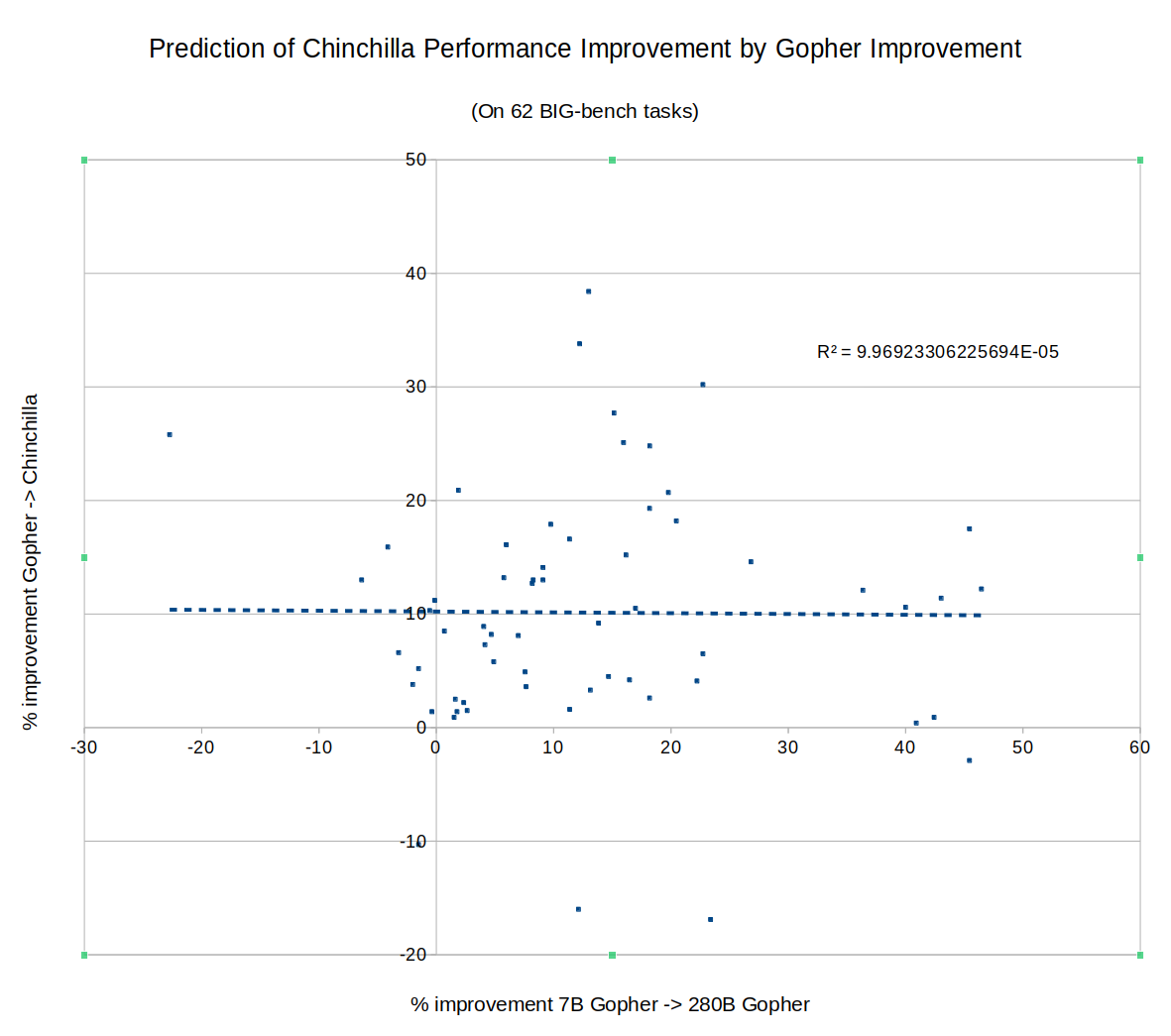
What about DeepMind's new Chinchilla? Did rapid improvement of a task on Gopher predict continued improvement going from Gopher to Chinchilla? Nope:
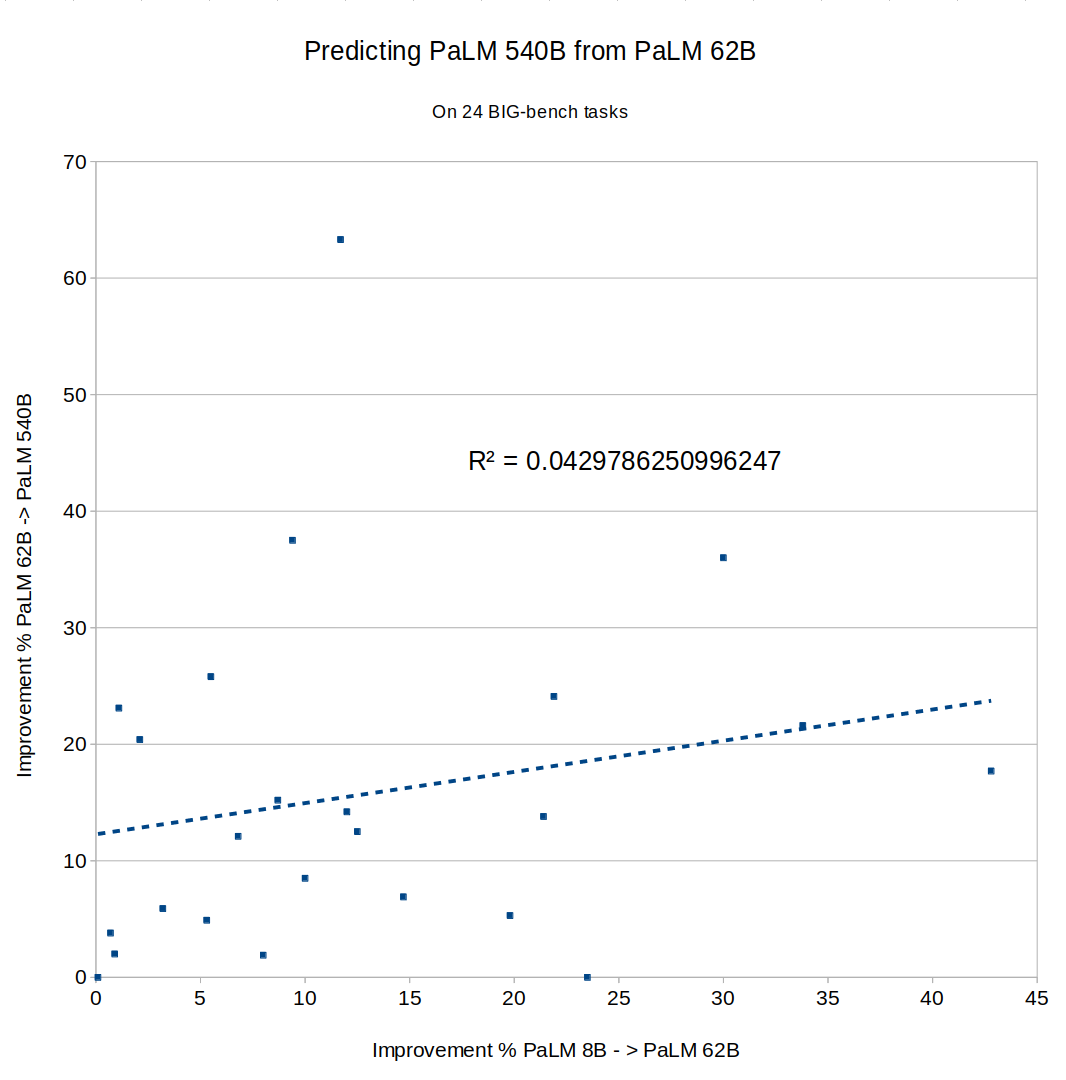
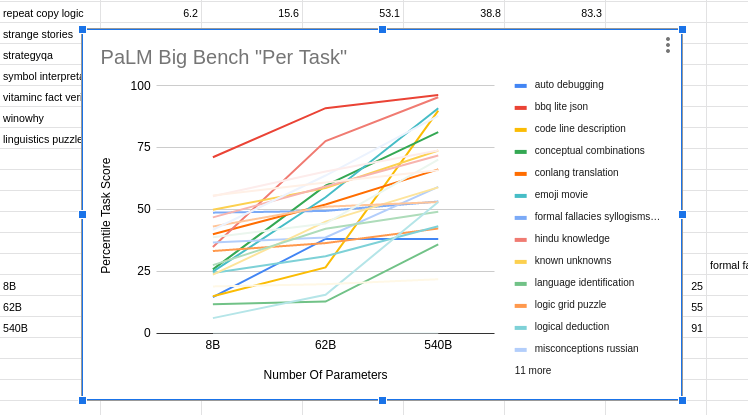
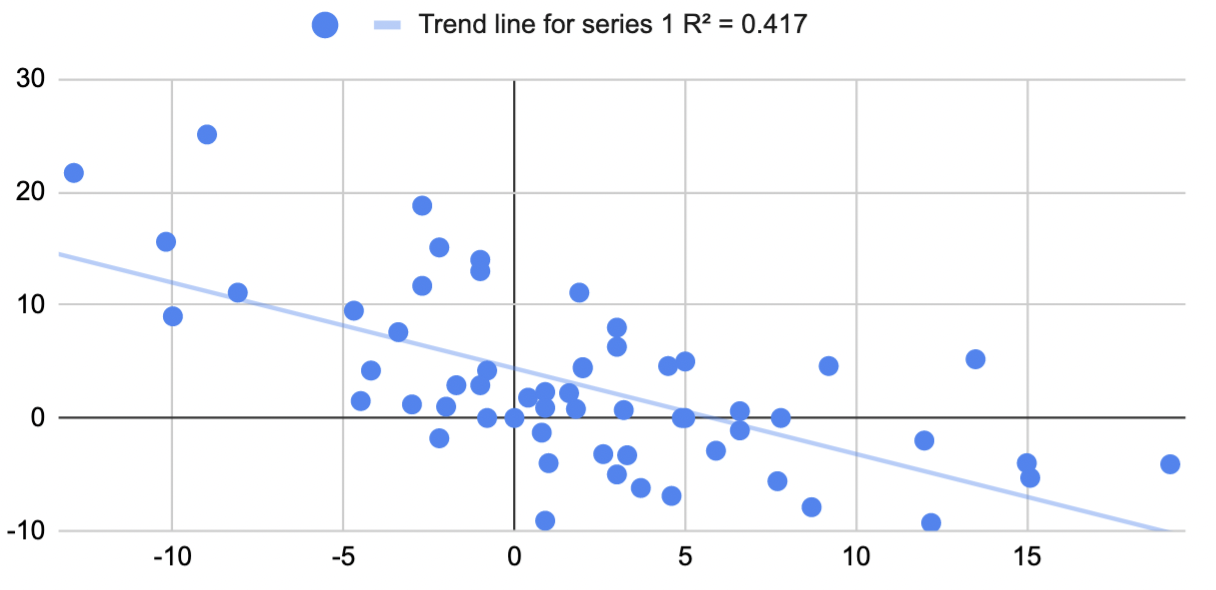
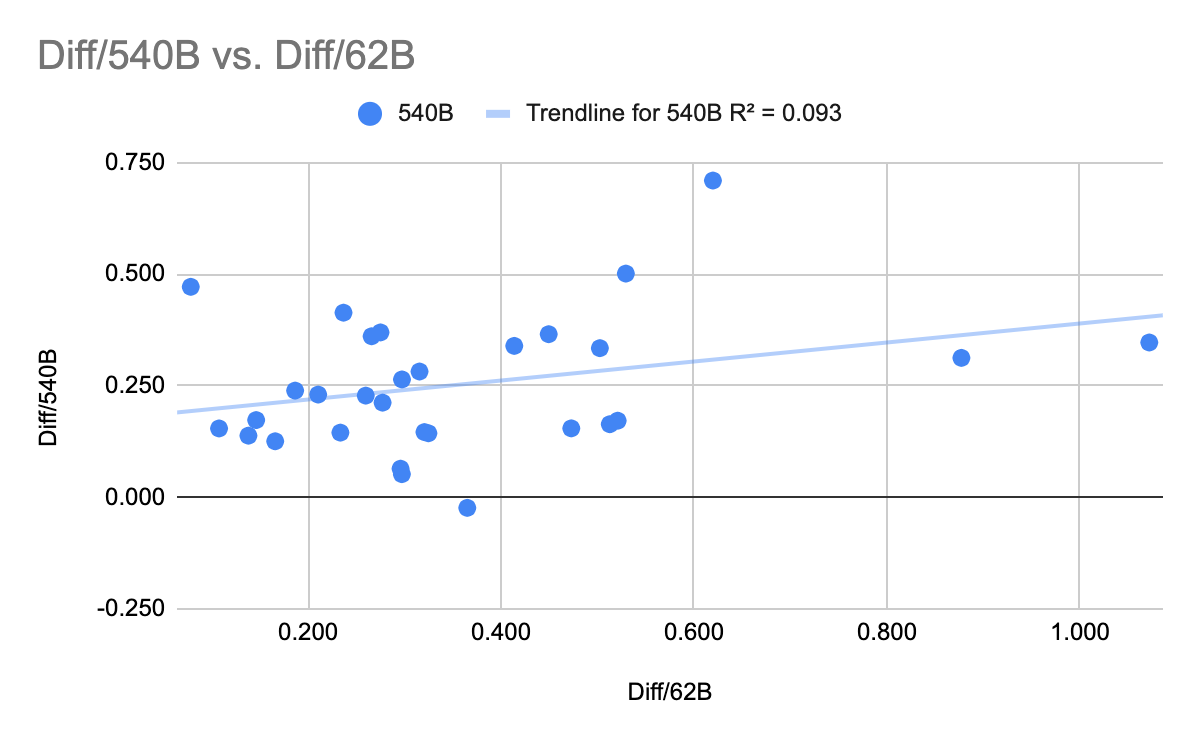
What about Google's PaLM? The full results of PaLM on BIG-bench don't seem to have been published yet, so I couldn't directly compare to Chinchilla or Gopher, but the PaLM paper described an 8B parameter model, a 62B model and a 540B model. Did fast improvement from 8B to 62B predict improvement from 62B to 540B? Not really, R^2 = 0.04:
PaLM also provides data on 30 different NLU benchmark tasks. Plot those and you get the same thing:
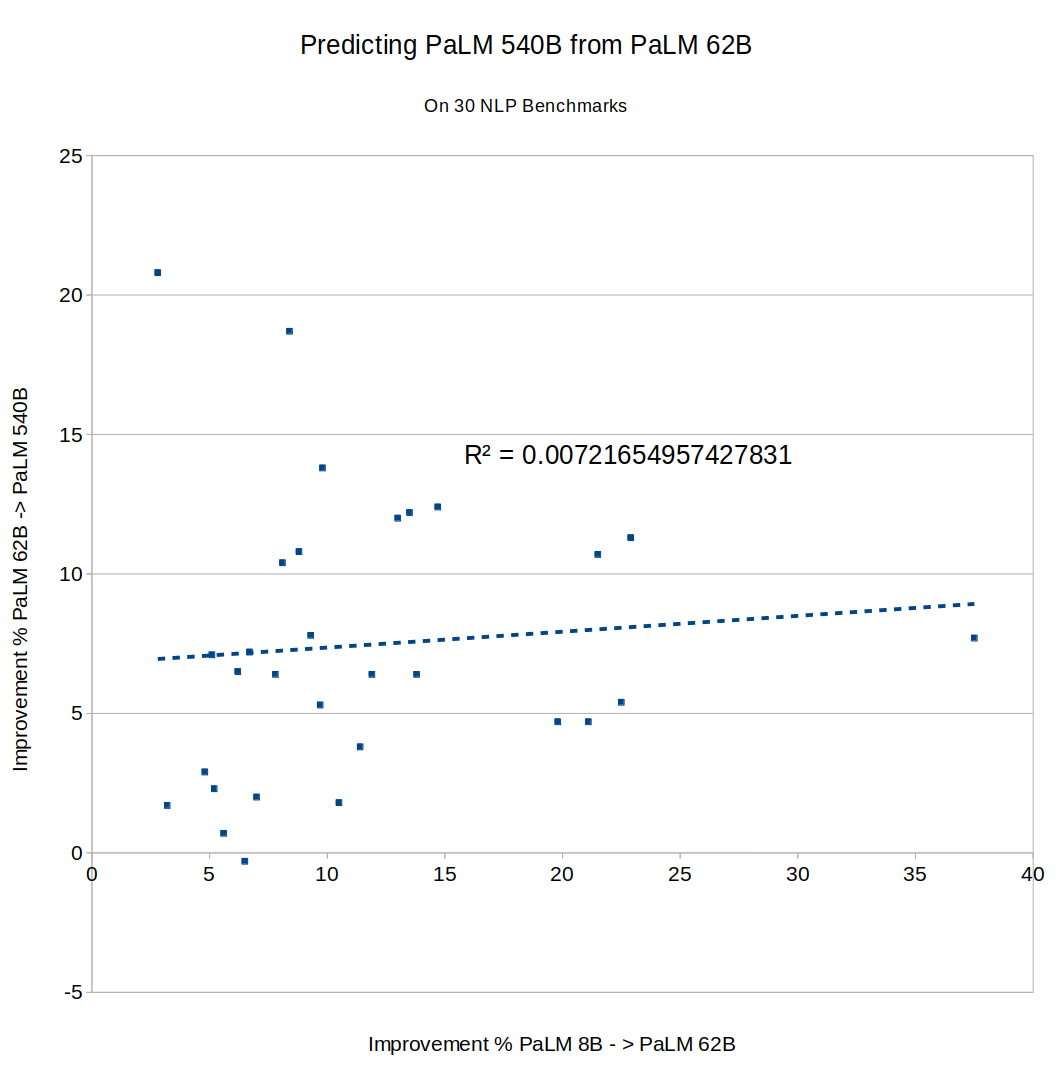
The results here seem pretty clear, but I'm honestly not sure how to interpret them. Before trying this, I assumed you would find that some tasks are "easy" and scale quickly, while others are "hard" and scale slowly. But that would get you high predictability, since fast progress between one pair of models would imply that the task is inherently "easy", and predict (perhaps with some noise) fast progress on the next pair. I didn't see that.
You could also have a theory where tasks scaled similarly (all are of comparable "difficulty"), but there was some noise between model training runs, so that task performance on any given run would bounce up and down around some "true" average value. (Since if you did badly on one run, you'd expect to regress to the mean, and do unusually well on the next.) But I didn't see that either. The two effects (some tasks being intrinsically easier, and individual model runs being noisy) could also cancel out, since one implies a positive correlation and the other implies a negative one... but it seems unlikely that they would exactly cancel every time!
Is AI task performance a type of submartingale, like a stock market index that goes up over time, but where each particular movement is intrinsically unpredictable? Maybe we can compare it to the growth in company profits, where the literature says that companies might grow slowly or quickly, but whether a company has grown fast recently has zero predictive power for future growth. I guess if we knew what we were doing, it wouldn't be called research.
EDIT: By request, here's a Google sheet with the raw data, copy-pasted from the Gopher, PaLM and Chinchilla papers: https://docs.google.com/spreadsheets/d/1Y_00UcsYZeOwRuwXWD5_nQWAJp4A0aNoySW0EOhnp0Y/edit?usp=sharing
EDIT 2: Several people suggested using logits instead of raw percentages. I tried that with the Gopher numbers, still got zero correlation:
EDIT 3: Tamay noted that if you try to predict 7B Gopher from 1B Gopher, you get a negative correlation:
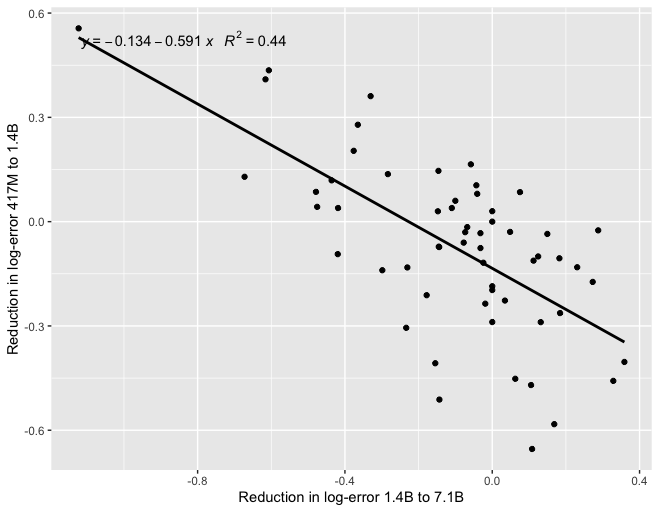
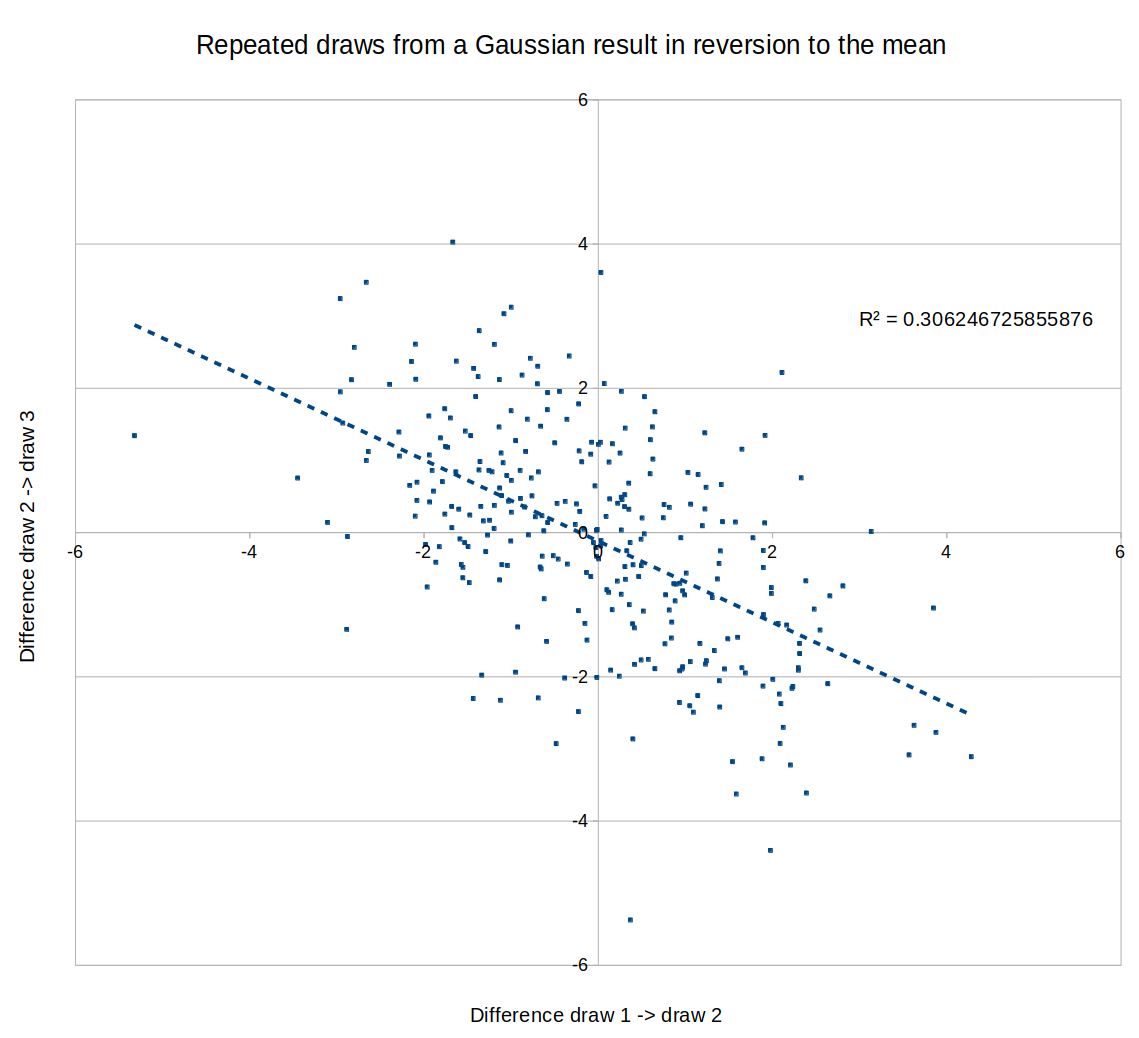
If the models become small enough, maybe this means that scale isn't helping you at that level, so the differences between performances are noise and you should expect mean reversion? Eg., here is a graph of a negative correlation between different "runs", where the "runs" are just draws from a random Gaussian:

I. FRAMING A RESPONSE CONCEPTUALLY
A starting assumption of mine is that a bigger and bigger model will not get better and better at tictactoe.
The task is fundamentally finite, and also, in this case, it is a simple task that will be saturated quickly and this is obvious by inspection.
This is just a generic supposition but it is a useful "bounded & easy" example that fits in a clear place in a 2x2 concept grid that has {bounded, infinite} X {easy, hard}.
So I'm pretty sure at least some "infinite & hard" versions exist. (However, also, humans are barely capable of doing this kind of stuff autonomously.)
Proof sketch based on Godel:
We know from "the incompleteness theorem" that second order predicate logic is "infinite" in some sense, because for all non-trivial sets of axioms you can find propositions in the implied logical universe that could be EITHER of true or false... and then the mathematician gets to pick which they like better, and either can be productively explored, and the mathematician will never get "stuck" with a system that contains no interesting propositions after making a choice.
(For example, Euclid's first four postulates define a game that leaves "parallel line" questions undecidable... and then mathematicians can, once they notice this choice, pick (using a fifth postulate) if they want to play in a playground that is: spherical, planar, or hyperbolic ...and they can keep doing that "notice choice, make choice" thing forever.
(Maybe it won't always be "aesthetically interesting" though? I don't currently know how to formalize mathematical aesthetics and prove things with the formalization of formalization. This is not needed for the more practical result however.))
So "infinite & hard" tasks are conceivable (though they might be pragmatically useless eventually, like how most people probably think of hyperbolic geometry as useless).
II. ORIENTING TO THIS DATA
It took me a while to orient to your data because the title led me to assume that each bigger model just got lower objective loss on its training data as the models got bigger, and...
...that's the end of that, and it has potentially pretty obvious trajectories I'd think?
...but after orienting I didn't find that much of the data to be that surprising, because it looks like the bulk of what's being measured here are a bunch of finite shards of human linguistic performance?!?
This isn't "AI progress" then, so much as "domain specific linguistic reasoning progress"... I think?
And... my assumption is that domain knowledge will mostly always be BOUNDED.
But the EASY/HARD part will potentially vary a lot from task to task?
The causal model here leads one to think about a generative model of AI language tasks difficulty would involve modeling human engineers and scientists doing human stuff, and it won't necessarily work sanely, especially if they do not currently (or have not in the past) really taken AGI seriously, and are not trying to design tasks that measure an approach to this outcome as the core thing to be interested in. Since many normal researchers have not been taking seriously for a very very long time, why would they do particularly any better now?
Backing out from the details about the people making the tasks... the obvious default here is that, for any given finite task, you would expect that performance on that task, scaled to resources/effort, will scale according to a logistic curve.
Indeed, the wikipedia article uses TASK PERFORMANCE SATURATION as its core example, for how "the concept of logistic regression" can be pragmatically approached.
So the thing I'd be looking for, naively, is any task specific curve that looks like this!
Assuming the prior is correct, non-naively, we seek falsification and look for things that COULD NOT be this!
III. APPLYING THE LOGISTIC CURVE FRAME TO THE DATA (TAKE 1)
I did find some in the raw data that was linked to.
The only dramatically obvious violation to my logistic regression prior is the dark blue one at the bottom (maybe "auto debugging"), which JUMPS UP from 8B Soto 62B but then seems to ALREADY SATURATE WELL BELOW 100% (and then actually goes slightly down on the 540B parameter model).
That specific task is a counter-example to what I expect.
That's where "I notice I'm confused" should kick in.
The thing I would do next, based on the strength of my priors, is treat that as a faulty task, and debug the task itself to make sure it wasn't two thirds full of "cheating questions" somehow.
A sane reasoner, presented with questions that are cheating, would eventually "notice the cheating" and "just guess" on those questions. In this case, by hypothesis, 1/3 of the "auto debugging" task questions are solvable, and the other 2/3s would be "password guessing" that are impossible to get right from coherent reasoning over a coherent body of accessible domain knowledge (such as was in the training data (like maybe the training data doesn't have much in it from car mechanics and car designers and maybe it doesn't have any transcripts from cartalk?)).
But I might be wrong. Maybe that task is NOT broken-via-bimodal-question-difficulty into "easy" and "impossible" questions?
Or maybe the sampling-over-model-sizes is too sparse to definitely rule in or out the logistic regression prior with no violations?
Or maybe my whole conceptual frame is broken?
But I don't think my concepts are missapplied here, and maybe it isn't just undersampling on the model size dimension... my max-liklihood hunch is that that task is "weird somehow".
Compared to that potential anomaly, every other task in this graph, by eyeball, looks consistent with having been sampled from a horizontal range of a logistic regression curve that ultimately asymptotes at 100%, with a linear-ish progress curve in the middle, and a starting state of "blind confusion and not even making much progress for a while in the lower left".
At the top, the red line makes it look like "bbq lite json" was already saturating with a mere 8B parameters, which is consistent with the asymptotic part of a logistic curve.
The strongly yellow-orange line of "code line description" looks like it was caught during the exponential takeoff. Also consistent.
A lot of them (like maybe that teal one that might be "emoji movie" that ends close to the top?) look basically linear in the observed range. The linear part, suggests that the "low progress confusion period" would only be visible off to the left and would take a small model to see, like one with only 1B parameters or 30M parameters.
Also the linear teal line has not looking saturated yet at the top left, and so it might be necessary to might need to do a 5T parameter model to see the logistic curve smooth out towards an asymptote of 100% performance?
That's the claim anyway.
III. APPLYING THE LOGISTIC CURVE FRAME TO THE DATA (TAKE 2)
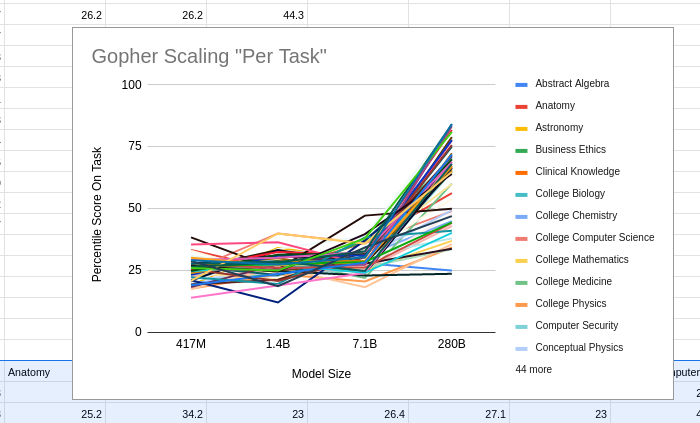
Looking at a different family of tasks and a different model's scaling performance...
Gopher looks to me, for these tasks, like it was thrashing around in "low level confusion" for ALL of the tasks, and then it started climbing on many of them in the last iteration with 280B parameters, but it hasn't saturated yet on ANY of the tasks, and would take a big bump (like maybe another 2 trillion, 30 trillion, or 200 trillion parameters?) to show the mastery/saturation start to occur for those tasks as well.
IV. A TANGENT INTO PSYCHOMETRICS
If there is any "I noticed I'm confused" aspect of this overall data, it would be that maybe the confused thrashing around should be happening closer to like 5% performance, instead of around 25% performance?
But you could maybe explain this by normal/correct psychometric test design principles, tilted towards modern academic culture which treats "half the class gets 50% of the questions right" as a social tragedy?
In a "clean" psychometric design (that doesn't worry about student hedonics), the goal is to SEPARATE the students based on differences in the students, and so you want a lot of binary questions close to "50% difficulty for these students".
But then worse students will fail on nearly all of these so you give them some questions that have "a 50/50 chance of help separate mastery of 10% of the content from 20% of the content" which are "wasted gimme questions" for the smarter students.
And then for better students, they will max ALL of these questions, and so if you actually want your A- to be meaningfully different from your A+ you need to have some questions that "a 50/50 chance of separating the students that mastered 92% of the content from 98% of the content".
Maybe all these Gopher tasks have "~25% gimme questions for the slow students" and not "5% gimme questions for the slow students"?
Oh! Insight after re-reading all of the above!
Probably what's happening is that there are multiple choice answers, with 4 options, and so 25% performance is overall the worst it can do by random guessing.
So maybe that's where the low end logistic curve thrashing is? <3
V. CONCLUSIONS AND DISCUSSION (technical... then deontic)
I didn't look closely at the other data sets for the other big models that have varying sizes.
Partly I wanted to save some data as "holdout" to check my reasoning against.
Maybe some of those models somehow falsify my high level "logistic regression over finite tasks is the right frame" prior?
BUT ALSO, the things I have written above (assuming they are correct) might help people understand the results of these big language models better, and design better tasks, and plan how to use their piles of money more efficiently to build smaller and better models that can do predictable tasks for predictable amounts of money.
IF you can calibrate the AI tasks (just like human-student performance tests that are good or bad as a psychometric measurement of domain mastery, with a logistic prior for all such tasks...
...THEN I think that would help plan capital expenditures for big model training runs more predictably?
But it isn't clear to me that such an outcome would be good?
I have been personally trying to not to make the march towards AGI go any farther or faster due to my own efforts...
...and this comment here is a VIOLATION of such a principle.
However, maybe I should stop caring so much. Assuming short timelines, large scale impacts on discourse might not matter so much any more?
I had another ~2500 words beyond this where I tried to do an equivalent amounts of reasoning that felt like maybe it could "make up" for the harm potentially done here, but I then figured I can always publish those words later (possibly with more polishing and better impacts) if it still makes sense to publish the rest later.
In the meantime... yeah, this data does not naively "look weird" to me or particularly "unpredictable"?
It just looks like (1) a pile of logistic regression curves for (2) different tasks with varying logistic curve parameters for different tasks... plus... (3) sparse sampling on the "effort" X-axis?
I think I endorse this condensation/steelman! Thank you for making it :-)
For more in this vein maybe: why forecasting S-curves is hard. The associated video is pretty great.