Epistemic status: Rambly; probably unimportant; just getting an idea that's stuck with me out there. Small dath-ilan-verse spoilers throughout, as well as spoilers for Sid Meier's Alpha Centauri (1999), in case you're meaning to get around to that.
The idea that's most struck me reading Yudkowsky et al.'s dath ilani fiction is the idea that dath ilan is puzzled by war. Theirs isn't a moral puzzlement; they're puzzled at how ostensibly intelligent actors could fail to notice that everyone can do strictly better if they could just avoid fighting and instead sign enforceable treaties to divide the resources that would have been spent or destroyed fighting.
This … isn't usually something that figures into our vision for the science-fiction future. Take Sid Meier's Alpha Centauri (SMAC), a game whose universe absolutely fires my imagination. It's a 4X title, meaning that it's mostly about waging and winning ideological space war on the hardscrabble space frontier. As the human factions on Planet's surface acquire ever more transformative technology ever faster, utterly transforming that world in just a couple hundred years as their Singularity dawns … they put all that technology to use blowing each other to shreds. And this is totally par for the course for hard sci-fi and the human future of the vision generally. War is a central piece of the human condition; always has been. We don't really picture that changing as we get modestly superintelligent AI. Millenarian ideologies that preach the end of war … so preach because of how things will be once they have completely won the final war, not because of game theory that could reach across rival ideologies. The idea that intelligent actors who fundamentally disagree with one another's moral outlooks will predictably stop fighting at a certain intelligence threshold not all that far above IQ 100, because fighting isn't Pareto optimal … totally blindsides my stereotype of the science-fiction future. The future can be totally free of war, not because any single team has taken over the world, but because we got a little smarter about bargaining.
Let's jump back to SMAC:

This is the game text that appears as the human factions on Planet approach their singularity. Because the first faction to kick off their singularity will have an outsized influence on the utility function inherited by their superintelligence, late-game war with horrifyingly powerful weapons is waged to prevent others from beating your faction to the singularity. The opportunity to make everything way better … creates a destructive race to that opportunity, waged with antimatter bombs and more exotic horrors.
I bet when dath ilan kicks off their singularity, they end up implementing their CEV in such a way as to not create an incentive for any one group to race to the end, to be sure my values aren't squelched if someone else gets there first. That whole final fight over the future can be avoided, since the overall value-pie is about to grow enormously! Everyone can have more of what they want in the end, if we're smart enough to think through our binding contracts now.
Moral of the story: beware of pattern matching the future you're hoping for to either more of the past or to familiar fictional examples. Smart, more agentic actors behave differently.
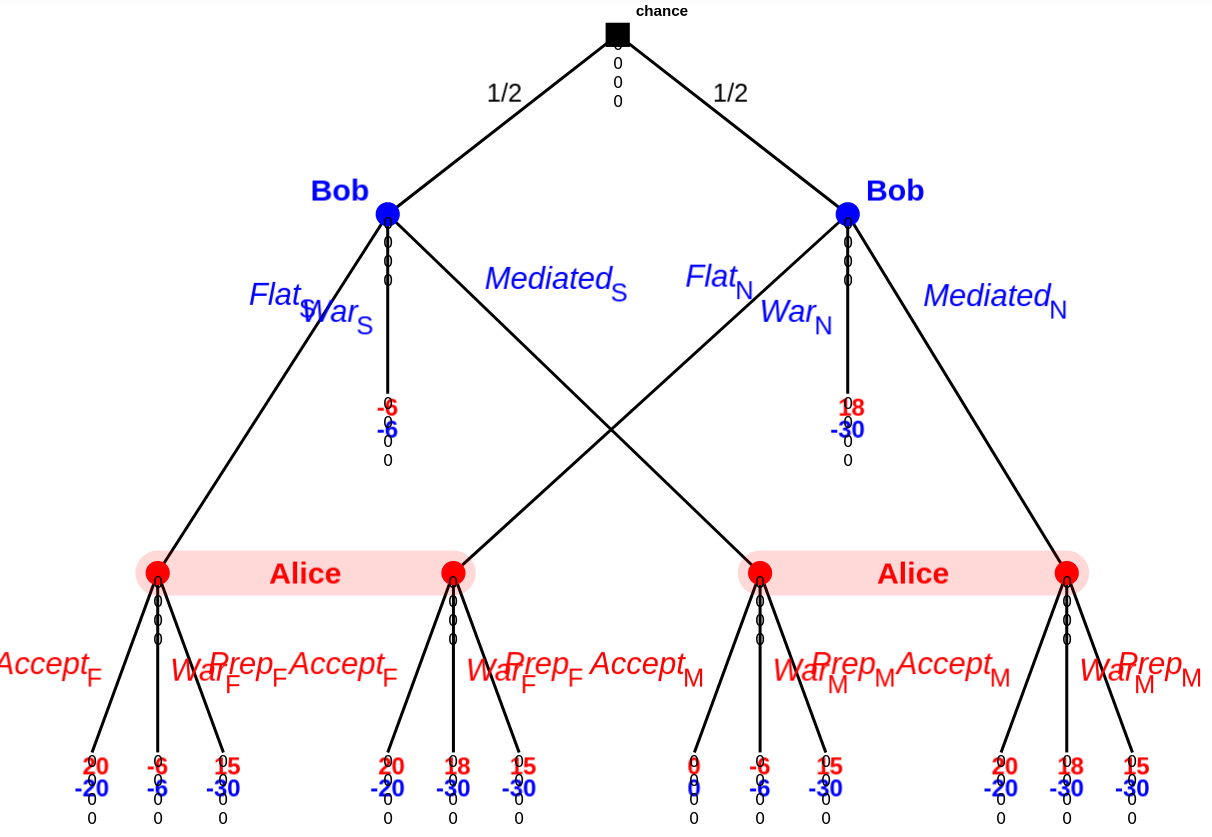
Here's an example game tree:
(Kindly ignore the zeros below each game node; I'm using the dev version of GTE, which has a few quirks.)
Roughly speaking:
Wars cost the winner 2 and the loser 10, and also transfers 20 from the loser to the winner. (So normally war is normally +18 / -30 for the winner/loser.).
Alice doing an audit/preparing costs 3, on top of the usual, regardless of if there's actually an exploit.
Alice wins all the time unless Bob has something up his sleeve and Alice doesn't prepare. (+18/-30, or +15/-30 if Alice prepared.) Even in that case, Alice wins 50% of the time. (-6 / -6). Bob has something up his sleeve 50% of the time.
Flat offer here means 'do the transfer as though there was a war, but don't destroy anything'. A flat offer is then always +20 for Alice and -20 for Bob.
Arbitrated means 'do a transfer based on the third party's evaluation of the probability of Bob winning, but don't actually destroy anything'. So if Bob has something up his sleeve, Charlie comes back with a coin flip and the result is 0, otherwise it's +20/-20.
There are some 17 different Nash equilibria here, with an EP from +6 to +8 for Alice and -18 to -13 for Bob. As this is a lot, I'm not going to list them all. I'll summarize:
Notably, Alice and Bob always offering/accepting an arbitrated agreement is not an equilibrium of this game[3]. None of these equilibria result in Alice and Bob always doing arbitration. (Also notably: all of these equilibria have the two sides going to war at least occasionally.)
There are likely other cases with different payoffs that have an equilibrium of arbitration/accepting arbitration; this example suffices to show that not all such games lead to said result as an equilibrium.
I use 'audit' in most of this; I used 'prep' for the game tree because otherwise two options started with A.
read: go 'uhoh' and spend a bunch of effort finding/fixing Bob's presumed exploit.
This is because, roughly, a Nash equilibrium requires that both sides choose a strategy that is best for them given the other party's response, but if Bob chooses MediatedS / MediatedN, then Alice is better off with PrepM over AcceptM. Average payout of 15 instead of 10. Hence, this is not an equilibrium.