This work looks super interesting, definitely keen to see more! Will you open-source your code for running the experiments and producing plots? I'd definitely be keen to play around with it. (They already did here: https://github.com/adamjermyn/toy_model_interpretability I just missed it. Thanks! Although it would be useful to have the plotting code as well, if that's easy to share?)
Note that we primarily study the regime where there are more features than embedding dimensions (i.e. the sparse feature layer is wider than the input) but where features are sufficiently sparse that the number of features present in any given sample is smaller than the embedding dimension. We think this is likely the relevant limit for e.g. language models, where there are a vast array of possible features but few are present in any given sample.
I agree that N (true feature dimension) > d (observed dimension), and that sparsity will be high, but I'm uncertain whether the other part of the regime (that you don't mention here), that k (model latent dimension) > N, is likely to be true. Do you think that is likely to be the case? As an analogy, I think the intermediate feature dimensions in MLP layers in transformers (analogously k) are much lower dimension than the "true intrinsic dimension of features in natural language" (analogously N), even if it is larger than the input dimension (embedding dimension* num_tokens, analogously d). So I expect whereas in your regime . Do you think you'd be able to find monosemantic networks for ? Did you try out this regime at all (I don't think I could find it in the paper).
In the paper you say that you weakly believe that monosemantic and polysemantic network parametrisations are likely in different loss basins, given they're implementing very different algorithms. I think (given the size of your networks) it should be easy to test for at least linear mode connectivity with something like git re-basin (https://github.com/samuela/git-re-basin). Have you tried doing that? I think there are also algorithms for finding non-linear (e.g. quadratic) mode connectivity, although I'm less familiar with them. If it is the case that they're in different basins, I'd be curious to see whether there are just two basins (poly vs mono), or a basin for each level of monosemanticity, or if even within a level of polysemanticity there are multiple basins. If it's one of the former cases, it's be interesting to do something like the connectivity-based fine-tuning talked about here (https://openreview.net/forum?id=NZZoABNZECq, in effect optimise for a new parametrisation that is linearly disconnected from the previous one), and see if doing that from a polysemantic initialisation can produce a more monosemantic one, or if it just becomes polysemantic in a different way.
You also mentioned your initial attempts at sparsity through a hard-coded initially sparse matrix failed; I'd be very curious to see whether a lottery ticket-style iterative magnitude pruning was able to produce sparse matrices from the high-latent-dimension monosemantic networks that are still monosemantic, or more broadly how the LTH interacts with polysemanticity - are lottery tickets less polysemantic, or more, or do they not really change the monosemanticity?
If my understanding of the bias decay method is correct, is a large initial part of training only reducing the bias (through weight decay) until certain neurons start firing? If that's the case, could you calculate the maximum output in the latent dimension on the dataset at the start of training (say B), and then initialise the bias to be just below -B, so that you skip almost all of the portion of training that's only moving the bias term. You could do this per-neuron or just maxing over neurons. Or is this portion of training relatively small compared to the rest of training, and the slower convergence is more due to less neurons getting gradients even when some of them are outputting higher than the bias?
Thanks for these thoughts!
Although it would be useful to have the plotting code as well, if that's easy to share?
Sure! I've just pushed the plot helper routines we used, as well as some examples.
I agree that N (true feature dimension) > d (observed dimension), and that sparsity will be high, but I'm uncertain whether the other part of the regime (that you don't mention here), that k (model latent dimension) > N, is likely to be true. Do you think that is likely to be the case? As an analogy, I think the intermediate feature dimensions in MLP layers in transformers (analogously k) are much lower dimension than the "true intrinsic dimension of features in natural language" (analogously N), even if it is larger than the input dimension (embedding dimension* num_tokens, analogously d). So I expect
This is a great question. I think my expectation is that the number of features exceeds the number of neurons in real-world settings, but that it might be possible to arrange for the number of neurons to exceed the number of important features (at least if we use some sparsity/gating methods to get many more neurons without many more flops).
If we can't get into that limit, though, it does seem important to know what happens when k < N, and we looked briefly at that limit in section 4.1.4. There we found that models tend to learn some features monosemantically and others polysemantically (rather than e.g. ignoring all but k features and learning those monosemantically), both for uniform and varying feature frequencies.
This is definitely something we want to look into more though, in particular in case of power-law (or otherwise varying) feature frequencies/importances. You might well expect that features just get ignored below some threshold and monosemantically represented above it, or it could be that you just always get a polysemantic morass in that limit. We haven't really pinned this down, and it may also depend on the initialization/training procedure (as we saw when k > N), so it's definitely worth a thorough look.
In the paper you say that you weakly believe that monosemantic and polysemantic network parametrisations are likely in different loss basins, given they're implementing very different algorithms. I think (given the size of your networks) it should be easy to test for at least linear mode connectivity with something like git re-basin (https://github.com/samuela/git-re-basin).
We haven't tried this. It's something we looked into briefly but were a little concerned about going down a rabbit hole given some of the discussion around whether the results replicated, which indicated some sensitivity to optimizer and learning rate.
I think (at least in our case) it might be simpler to get at this question, and I think the first thing I'd do to understand connectivity is ask "how much regularization do I need to move from one basin to the other?" So for instance suppose we regularized the weights to directly push them from one basin towards the other, how much regularization do we need to make the models actually hop?
Actually, one related reason we think that these basins are unlikely to be closely connected is that we see the monosemanticity "converge" towards the end of long training runs, rather than e.g. drifting as the model moves along a ridge. We don't see this convergence everywhere, and in particular in high-k power-law models we see continuing evolution after many steps, but we think we understand that as a refinement of a particular minimum to better capture infrequent features.
You also mentioned your initial attempts at sparsity through a hard-coded initially sparse matrix failed; I'd be very curious to see whether a lottery ticket-style iterative magnitude pruning was able to produce sparse matrices from the high-latent-dimension monosemantic networks that are still monosemantic, or more broadly how the LTH interacts with polysemanticity - are lottery tickets less polysemantic, or more, or do they not really change the monosemanticity?
Good question! We haven't tried that precise experiment, but have tried something quite similar. Specifically, we've got some preliminary results from a prune-and-grow strategy (holding sparsity fixed, pruning smallest-magnitude weights, enabling non-sparse weights) that does much better than a fixed sparsity strategy.
I'm not quite sure how to interpret these results in terms of the lottery ticket hypothesis though. What evidence would you find useful to test it?
You might well expect that features just get ignored below some threshold and monosemantically represented above it, or it could be that you just always get a polysemantic morass in that limit
I guess the recent work on Polysemanticity and Capacity seems to suggest the latter case, especially in sparser settings, given the zone where multiple feature are represented polysemantically, although I can't remember if they investigate power-law feature frequencies or just uniform frequencies
were a little concerned about going down a rabbit hole given some of the discussion around whether the results replicated, which indicated some sensitivity to optimizer and learning rate.
My impression is that that discussion was more about whether the empirical results (i.e. do ResNets have linear mode connectivity?) held up, rather than whether the methodology used and present in the code base could be used to find whether linear mode connectivity is present between two models (up to permutation) for a given dataset. I imagine you could take the code and easily adapt it to check for LMC between two trained models pretty quickly (it's something I'm considering trying to do as well, hence the code requests).
I think (at least in our case) it might be simpler to get at this question, and I think the first thing I'd do to understand connectivity is ask "how much regularization do I need to move from one basin to the other?" So for instance suppose we regularized the weights to directly push them from one basin towards the other, how much regularization do we need to make the models actually hop?
That would defiitely be interesting to see. I guess this is kind of presupposing that the models are in different basins (which I also believe but hasn't yet been verified). I also think looking at basins and connectivity would be more interesting in the case where there was more noise, either from initialisation, inherently in the data, or by using a much lower batch size so that SGD was noisy. In this case it's less likely that the same configuration results in the same basin, but if your interventions are robust to these kinds of noise then it's a good sign.
Good question! We haven't tried that precise experiment, but have tried something quite similar. Specifically, we've got some preliminary results from a prune-and-grow strategy (holding sparsity fixed, pruning smallest-magnitude weights, enabling non-sparse weights) that does much better than a fixed sparsity strategy.
I'm not quite sure how to interpret these results in terms of the lottery ticket hypothesis though. What evidence would you find useful to test it?
That's cool, looking forward to seeing more detail. I think these results don't seem that related to the LTH (if I understand your explanation correctly), as LTH involves finding sparse subnetworks in dense ones. Possibly it only actually holds in model with many more parameters, I haven't seen it investigated in models that aren't overparametrised in a classical sense.
I think if iterative magnitude pruning (IMP) on these problems produced much sparse subnetworks that also maintained the monosemanticity levels, then that would suggest that sparsity doesn't penalise monosemanticity (or polysemanticity) in this toy model, and also (much more speculatively) that the sparse well-performing subnetworks that IMP finds in other networks possibly also maintain their levels of poly/mono-semanticity. If we also think these networks are favoured towards poly or mono, then that hints at how the overall learning process if favoured towards poly or mono.
In case you haven't seen it, it looks like there's a separate strain of work somewhat along these lines from Zhi Chen and others, under the name "concept whitening." You may already be aware of it, but I thought I'd pass it along in case not.
[Concept Whitening for Interpretable Image Recognition](https://arxiv.org/pdf/2002.01650.pdf)
Great stuff!
Do you have results with noisy inputs?
The negative bias lines up well with previous sparse coding implementations: https://scholar.google.com/citations?view_op=view_citation&hl=en&user=JHuo2D0AAAAJ&citation_for_view=JHuo2D0AAAAJ:u-x6o8ySG0sC
Note that in that research, the negative bias has a couple of meanings/implications:
Along those lines, you might be able to further improve monosemanticity by using the lasso loss function.
Do you have results with noisy inputs?
Nope! Do you have predictions for what noise might do here?
The negative bias lines up well with previous sparse coding implementations: https://scholar.google.com/citations?view_op=view_citation&hl=en&user=JHuo2D0AAAAJ&citation_for_view=JHuo2D0AAAAJ:u-x6o8ySG0sC
Oooo I'll definitely take a look. This looks very relevant.
Note that in that research, the negative bias has a couple of meanings/implications:
- It should correspond to the noise level in your input channel.
- Higher negative biases directly contribute to the sparsity/monosemanticty of the network.
We don't have any noise, but we do think that the bias is serving a de-interference role (because features get packed together in a space that's not big enough to avoid interference).
Along those lines, you might be able to further improve monosemanticity by using the lasso loss function.
Can you say more about why? We know that L1 regularization on the activations (or weights) increases monosemanticity, but why do you think this would happen when done as part of the task loss?
My weak prediction is that adding low levels of noise would change the polysemantic activations, but not the monosemantic ones.
Adding L1 to the loss allows the network to converge on solutions that are more monosemantic than otherwise, at the cost of some estimation error. Basically, the network is less likely to lean on polysemantic neurons to make up small errors. I think your best bet is to apply the L1 loss on the hidden layer and the output later activations.
Overview
In some neural networks, individual neurons correspond to natural "features" in the input. Such monosemantic neurons are much easier to interpret, because in a sense they only do one thing. By contrast, some neurons are polysemantic, meaning that they fire in response to multiple unrelated features in the input. Polysemantic neurons are much harder to characterize because they can serve multiple distinct functions in a network.
Recently, Elhage+22 and Scherlis+22 demonstrated that architectural choices can affect monosemanticity, raising the prospect that we might be able to engineer models to be more monosemantic. In this work we report preliminary attempts to engineer monosemanticity in toy models.
Toy Model
The simplest architecture that we could study is a one-layer model. However, a core question we wanted to answer is: how does the number of neurons (nonlinear units) affect the degree of monosemanticity? To that end, we use a two-layer architecture:
Features are generated as sparse vectors in a high-dimensional space. They are then run through a (fixed) random projection layer to produce the inputs into our model. We imagine this random projection process as an analogy to the way the world encodes features in our observations.
Within the model, the first layer is a linear transformation with a bias, followed by a nonlinearity. The second layer is a linear transformation with no bias.
Our toy model is most similar to that of Elhage+22, with a key difference being that the extra linear layer allows us to vary the number of neurons independent of the number of features or the input dimension.
We study this two model on three tasks. The first, a feature decoder, performs a compressed sensing reconstruction of features that were randomly and lossily projected into a low-dimensional space. The second, a random re-projector, reconstructs one fixed random projection of features from a different fixed random projection. The third, an absolute value calculator, performs the same compressed sensing task and then returns the absolute values of the recovered features. These tasks have the important property that we know which features are naturally useful, and so can easily measure the extent to which neurons are monosemantic or polysemantic.
Note that we primarily study the regime where there are more features than embedding dimensions (i.e. the sparse feature layer is wider than the input) but where features are sufficiently sparse that the number of features present in any given sample is smaller than the embedding dimension. We think this is likely the relevant limit for e.g. language models, where there are a vast array of possible features but few are present in any given sample.
Key Results
We find that models initialized with zero mean bias (left) find different local minima depending on the learning rate, with more monosemantic solutions and slightly lower loss at higher learning rates. Models initialized with a negative mean bias (right) all find highly monosemantic local minima, and achieve slightly better loss. Note that these models are all in a regime where they have more neurons than there are input features.
Just to hammer home how weird this is, below we've plotted the activations of neurons in response to single-feature inputs. The three models we show get essentially the same loss but are clearly doing very different things!
More generally, we find:
Interpretability
In Section 5 we provide some mechanistic interpretability results for our feature decoder models in the monosemantic limit. In this toy model setting we can decompose our model into a monosemantic part and a polysemantic part, and plotting these separately feature-by-feature is revealing:
From this, we find that:
Additionally, we were suspicious at how few kinks the polysemantic neurons provided to the model's output. Indeed plotting the linearized map that these neurons implement reveals that they primarily serve to implement a low-rank approximation to the identity, which allows the model to have non-zero confidence in features at low input amplitudes: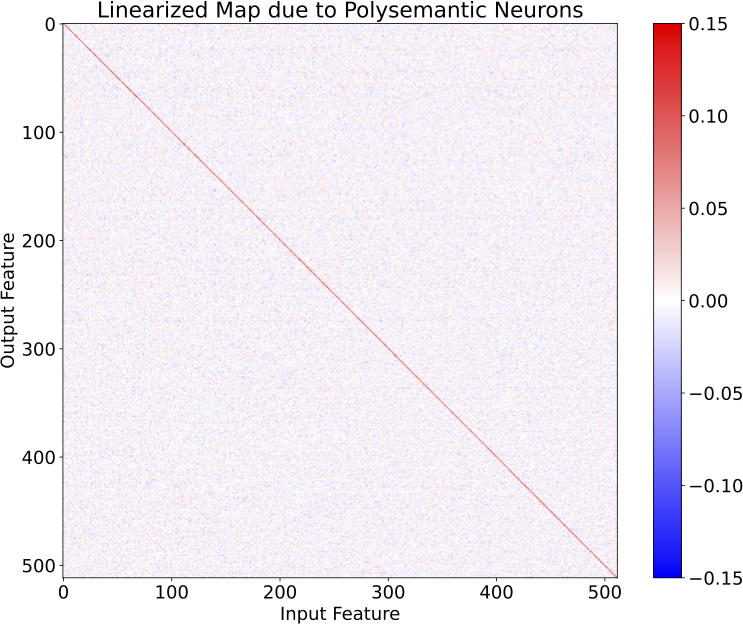
Future Work
We think there's a lot of low-hanging fruit in the direction of "engineer models to be more monosemantic", and we're excited to pick some more of it. The things we're most excited about include:
We'd be excited to answer questions about our work or engage with comments/suggestions for future work, so please don't be shy!