I have a long and confused love-hate relationship with the field of complex systems. People there never want to give me a simple, straightforward explanation about what its about, and much of what they say sounds a lot like woo ("edge of chaos" anyone?). But it also seems to promise a lot! This from the primary textbook on the subject:
The present situation can be compared to an archaeological project, where a mosaic floor has been discovered and is being excavated. While the mosaic is only partly visible and the full picture is still missing, several facts are becoming clear: the mosaic exists; it shows identifiable elements (for instance, people and animals engaged in recognizable activities); there are large patches missing or still invisible, but experts can already tell that the mosaic represents a scene from, say, Homer’s Odyssey. Similarly, for dynamical complex adaptive systems, it is clear that a theory exists that, eventually, can be fully developed.
Of course, that textbook never actually described what the mosaic it thought it saw actually was. The closest it came to was:
More formally, co-evolving multiplex networks can be written as, [...] The second equation specifies how the interactions evolve over time as a function that depends on the same inputs, states of elements and interaction networks. can be deterministic or stochastic. Now interactions evolve in time. In physics this is very rarely the case. The combination of both equations makes the system a co-evolving complex system. Co-evolving systems of this type are, in general, no longer analytically solvable.
Which... well... isn't very exciting, and as far as I can tell just describes any dynamical system (co-evolving or no).
The textbook also seems pretty obsessed with a few seemingly random fields:
- Economics
- Sociology
- Biology
- Evolution
- Neuroscience
- AI
- Probability theory
- Ecology
- Physics
- Chemistry
"What?" I had asked, and I started thinking
Ok, I can see why some of these would have stuff in common with others.
Physics brings in a bunch of math you can use.
Economics and sociology both tackle similar questions with very different techniques. It would be interesting to look at what they can tell each other (though it seems strange to spin off a brand new field out of this).
Biology, evolution, and ecology? Sure. Both biology and ecology are constrained by evolutionary pressures, so maybe we can derive new things about each by factoring through evolution.
AI, probability theory, and neuroscience? AI and neuroscience definitely seem related. The history of AI and probability theory has been mixed, and I don't know enough about the history of neuroscience and probability theory to have a judgement there.
And chemistry??? Its mostly brought into the picture to talk about stoichiometry, the study of the rate and equilibria of chemical reactions. Still, what?
And how exactly is all this meant to fit together again?
And each time I heard a complex systems theorist talk about why their field was important they would say stuff like
Complexity spokesperson: Well, current classical economics mostly assumes you are in an economic equilibrium, this is because it makes the math easier, but in fact we're not! And similarly with a bunch of other fields! We make a bunch of simplifying assumptions, but they're all usually a simplification of the truth! Thus, complex systems science.
Me: Oh... so you don't make any simplifying assumptions? That seems... intractable?
Complexity spokesperson: Oh no our models still make plenty of simplifications, we just run a bunch of numerical simulations of toy scenarios, then make wide and sweeping claims about the results.
Me: That seems... worse?
Complexity spokesperson: Don't worry, our claims are usually of the form "and therefore X is hard to predict"
Me: Ok, a bit of a downer, but I guess scientific publishing needs more null results like that. So I guess you don't really expect your field to be all that useful when it comes to actually object-level predicting or controlling the world, more to serve as a guide to the limits of discovery?
Complexity Spokesperson: Well... not exactly, we do also have the economic complexity index which has actually been a better predictor of GDP growth than any other metric, which Hidalgo & Hausmann derived based on some nice network theory.
Me: I notice I am very, very confused.
That is, until I found this podcast with David Krakauer[1].
Now, to be clear, his framing of complex systems science is... lets say... controversial. But he is the president of the Santa Fe Institute, so not just some crackpot[2]. Anyway, he says that the phrase "complex systems" is a shortening of the more accurate phrase "complex adaptive systems". That is, complex systems are adaptive systems which are complex.
Ok, what does complex mean? I'll leave it to David to explain
0:06:45.9 DK: Yeah, so the important point is to recognize that we need a fundamentally new set of ideas where the world we're studying is a world with endogenous ideas. We have to theorize about theorizers and that makes all the difference. And so notions of agency or reflexivity, these kinds of words we use to denote self-awareness or what does a mathematical theory look like when that's an unavoidable component of the theory. Feynman and Murray both made that point. Imagine how hard physics would be if particles could think. That is essentially the essence of complexity. And whether it's individual minds or collectives or societies, it doesn't really matter. And we'll get into why it doesn't matter, but for me at least, that's what complexity is. The study of teleonomic matter. That's the ontological domain. And of course that has implications for the methods we use. And we can use arithmetic but we can also use agent-based models, right? In other words, I'm not particularly restrictive in my ideas about epistemology, but there's no doubt that we need new epistemology for theorizers. I think that's quite clear.
Now we can go back to our list:
- Economics
- Sociology
- Biology
- Evolution
- Neuroscience
- AI
- Probability theory
- Ecology
- Physics
- Chemistry
And its pretty clear how this ties together. Each field provides new math and data on the same underlying question: How would particles interact if they could "think"? Some of the above provides more foundational stuff (physics, probability theory, chemistry--in particular the study of equilibria and bottlenecks), and others provide more high-level stuff (economics, sociology, evolution, AI), but its all clearly related under this banner.
h/t Nora_Ammann ↩︎
Insofar as complex systems scientists aren't crackpots to begin with ↩︎
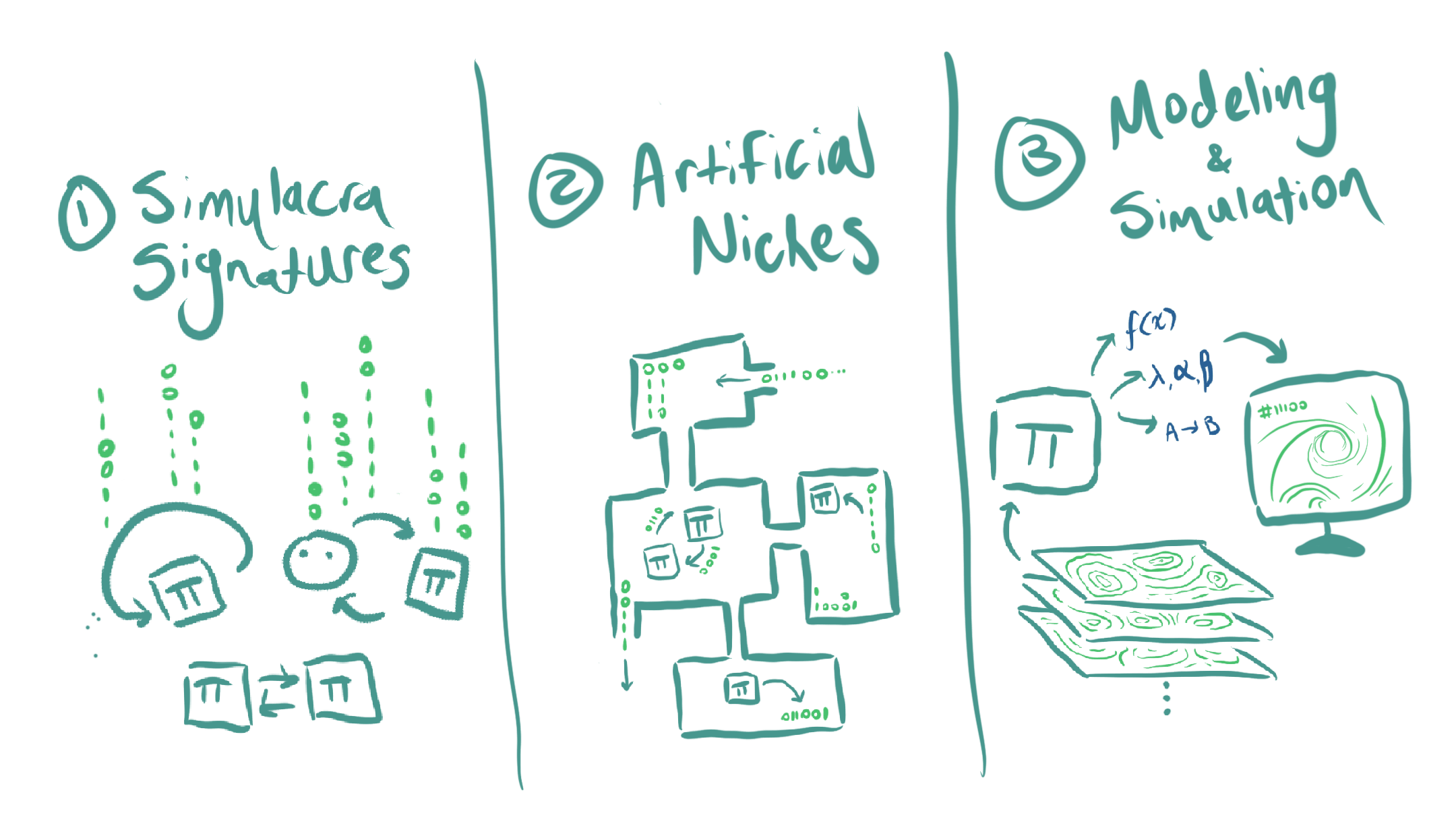
I spent a bit of time reading the first few chapters of Complexity: A Guided Tour. The author (also at the Santa Fe institute) claimed that, basically, everyone has their own definition of what "complexity" is, the definitions aren't even all that similar, and the field of complexity science struggles because of this.
However, she also noted that it's nothing to be (too?) ashamed of: other fields have been in similar positions, have come out ok, and that we shouldn't rush to "pick a definition and move on".
That doesn't really seem to me to hit the nail on the head.
I get the idea of how in physics, if billiards balls could think and decide what to do it'd be much tougher to predict what will happen. You'd have to think about what they will think.
On the other hand, if a human does something to another human, that's exactly the situation we're in: to predict what the second human will do we need to think about what the second human is thinking. Which can be difficult.
Let's abstract this out. Instead of billiards balls and humans we have parts. Well, really we have collections of parts. A billiard ball isn't one part, it consists of many atoms. Many other parts. So the question is of what one collection of parts will do after it is influenced by some other collection of parts.
If the system of parts can think and act, it makes it difficult to predict what it will do, but that's not the only thing that can make it difficult. It sounds to me like difficulty is the essence here, not necessarily thinking.
For example, in physics suppose you have one fluid that comes into contact with another fluid. It can be difficult to predict whether things like eddies or vortices will form. And this happens despite the fact that there is no "theorizing about theorizers".
Another example: if is often actually quite easy to predict what a human will do even though that involves theorizing about a theorizer. For example, if Employer stopped paying John Doe his salary, I'd have an easy time predicting that John Doe would quit.
Hm, good points.
I didn't mean to propose the difficulty frame as the answer to what complexity is really about. Although I'm realizing now that I kinda wrote it in a way that implied that.
I think what I'm going for is that "theorizing about theorizers" seems to be pointing at something more akin to difficulty than truly caring about whether the collection of parts theorizes. But I expect that if you poke at the difficulty frame you'll come across issues (like you have begun to see).