Current best guess: Nearly all the time.
"Correlation ⇏ Causation" is trite by now. And we also know that the contrapositive is false too: "¬Correlation ⇏ ¬Causation".
Spencer Greenberg summarizes:
All of this being said, while causation does not NECESSARILY imply correlation, causation USUALLY DOES imply correlation. Some software that attempts to discover causation in observational data even goes so far as to make this assumption of causation implying correlation.
I, however, have an inner computer scientist.
And he demands answers.
He will not rest until he knows how often ¬Correlation ⇒ ¬Causation, and how often it doesn't.
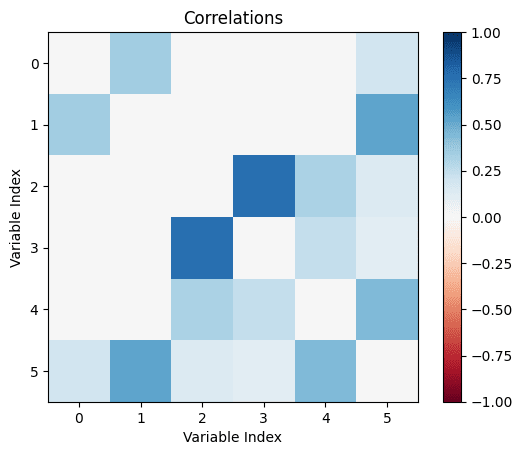
This can be tested by creating a Monte-Carlo simulation over random linear structural equation models with variables, computing the correlations between the different variables for random inputs, and checking whether the correlations being zero implies that there is no causation.
So we start by generating a random linear SEM with variables (code in Julia). The parameters are normally distributed with mean 0 and variance 1.
function generate_random_linear_sem(n::Int)
g = DiGraph(n)
for i in 1:n
for j in (i+1):n
if rand() < 0.5
add_edge!(g, i, j)
end
end
end
coefficients = Dict()
for edge in edges(g)
coefficients[edge] = randn()
end
return g, coefficients
end
We can then run a bunch of inputs through that model, and compute their correlations:
function correlation_in_sem(sem::DiGraph, coefficients::Dict, inner_samples::Int)
n = size(vertices(sem), 1)
input_nodes = [node for node in vertices(sem) if indegree(sem, node) == 0]
results = Matrix{Float64}(undef, inner_samples, n) # Preallocate results matrix
for i in 1:inner_samples
input_values = Dict([node => randn() for node in input_nodes])
sem_values=calculate_sem_values(sem, coefficients, input_values)
sem_value_row = reshape(collect(values(sort(sem_values))), 1, :)
results[i, :] = sem_value_row
end
correlations=cor(results)
for i in 1:size(correlations, 1)
correlations[i, i] = 0
end
return abs.(correlations)
end
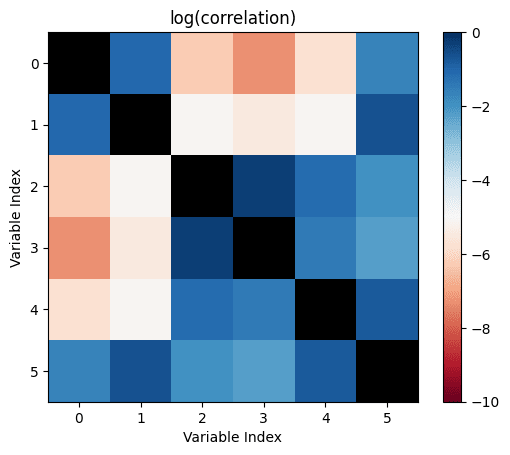
We can then check how many correlations are "incorrectly small".
Let's take all the correlations between variables which don't have any causal relationship. The largest of those is the "largest uncaused correlation". Correlations between two variables which cause each other but are smaller than the largest uncaused correlation are "too small": There is a causation but it's not detected.
We return the amount of those:
function misclassifications(sem::DiGraph, coefficients::Dict, inner_samples::Int)
correlations=correlation_in_sem(sem, coefficients, inner_samples)
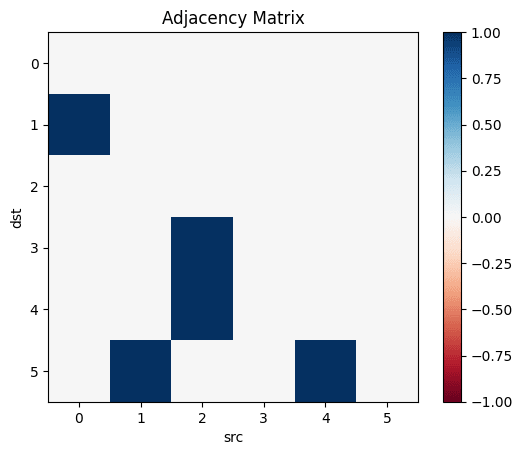
influence=Matrix(Bool.(transpose(adjacency_matrix(transitiveclosure(sem)))))
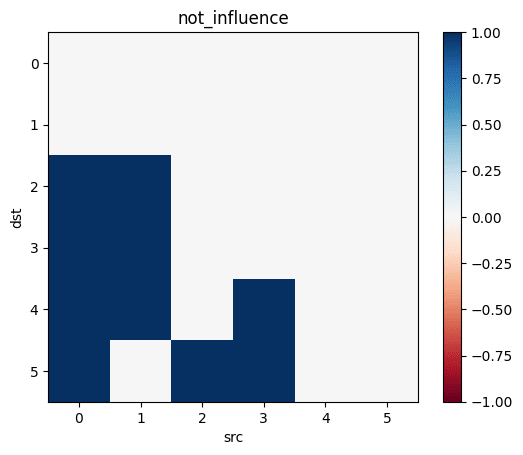
not_influence=tril(.!(influence), -1)
non_causal_correlations=not_influence.*correlations
causal_correlations=influence.*correlations
return sum((causal_correlations .!= 0) .& (causal_correlations .< maximum(non_causal_correlations)))
end
And, in the outermost loop, we compute the number of misclassifications for a number of linear SEMs:
function misclassified_absence_mc(n::Int, outer_samples::Int, inner_samples::Int)
return [misclassifications(generate_random_linear_sem(n)..., inner_samples) for i in 2:outer_samples]
end
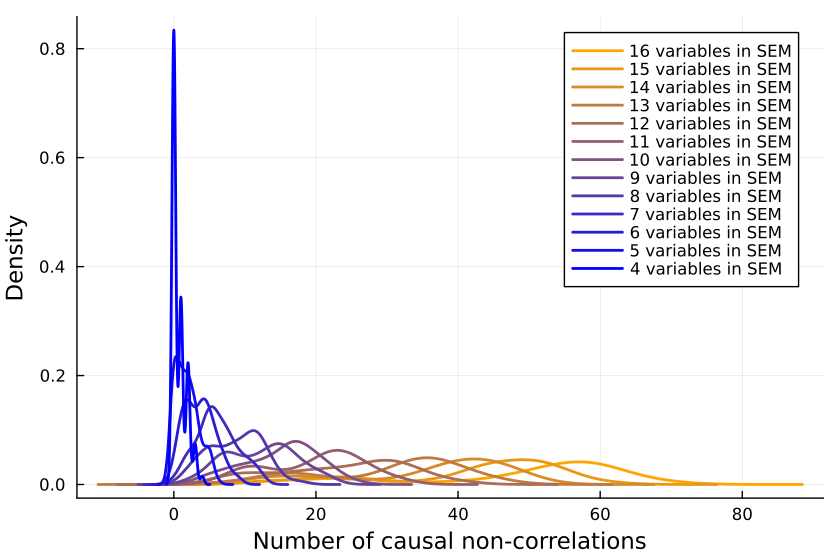
So we collect a bunch of samples. SEMs with one, two and three variables are ignored because when running the code, they never give me any causal non-correlations. (I'd be interested in seeing examples to the contrary.)
results = Dict{Int, Array{Int, 1}}()
sem_samples=200
inputs_samples=20000
for i in 4:16
results[i]=misclassified_absence_mc(i, sem_samples, inputs_samples)
end
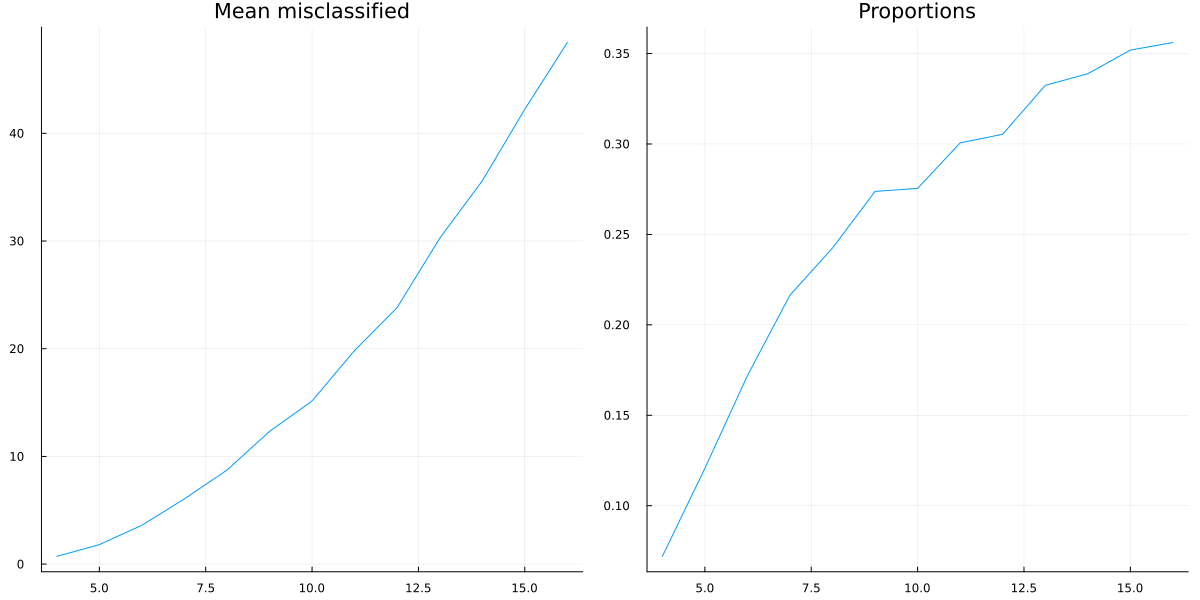
We can now first calculate the mean number of mistaken correlations and the proportion of misclassified correlations, using the formula for the triangular number:
result_means=[mean(values) for (key, values) in sort(results)]
result_props=[mean(values)/((key^2+key)/2) for (key, values) in sort(results)]
So it looks like a growing proportion of causal relationships are not correlational, and I think the number will asymptote to include almost all causal relations.
It could also be that the proportion asymptotes to another percentage, but I don't think so.
Is the Sample Size Too Small?
Is the issue with the number of inner samples, are we simply not checking enough? But 10k samples ought to be enough for anybody—if that's not sufficient, I don't know what is.
But let's better go and write some code to check:
more_samples=Dict{Int, Array{Int, 1}}()
samples_test_size=12
sem_samples=100
inputs_samples=2 .^(6:17)
for inputs_sample in inputs_samples
println(inputs_sample)
more_samples[inputs_sample]=misclassified_absence_mc(samples_test_size, sem_samples, inputs_sample)
end
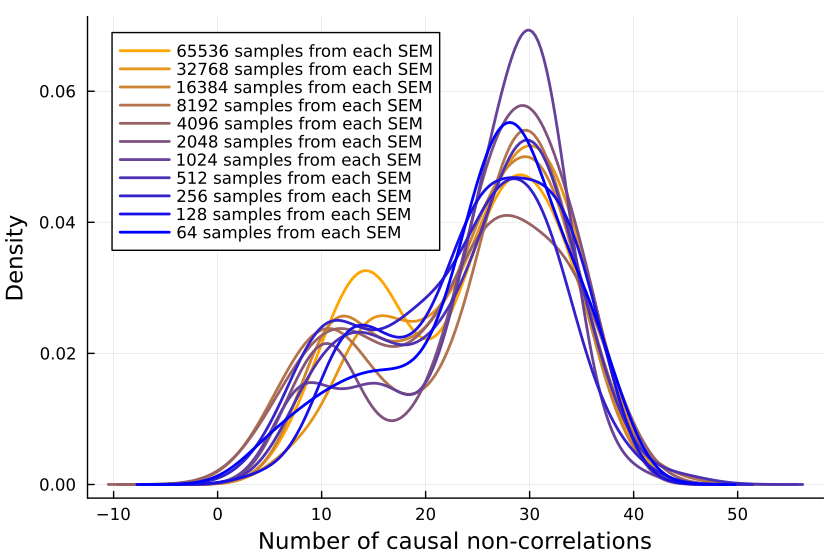
Plotting the number of causal non-correlations reveals that 10k samples ought to be enough, at least for small numbers of variables:
The densities fluctuate, sure, but not so much that I'll throw out the baby with the bathwater. If I was a better person, I'd make a statistical test here, but alas, I am not.

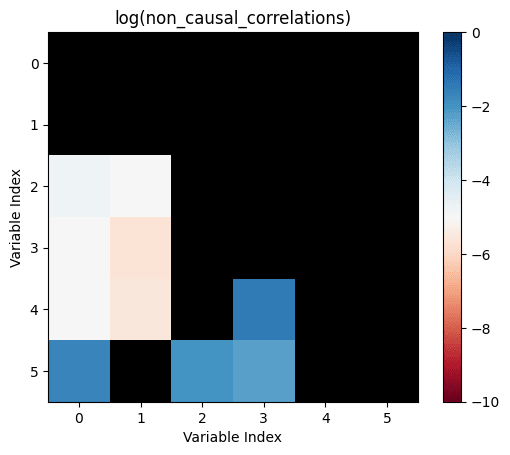
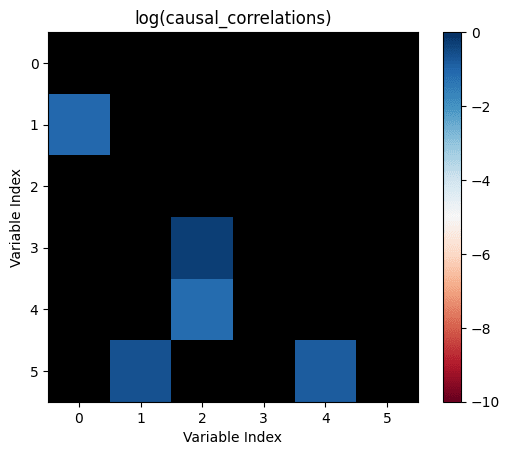
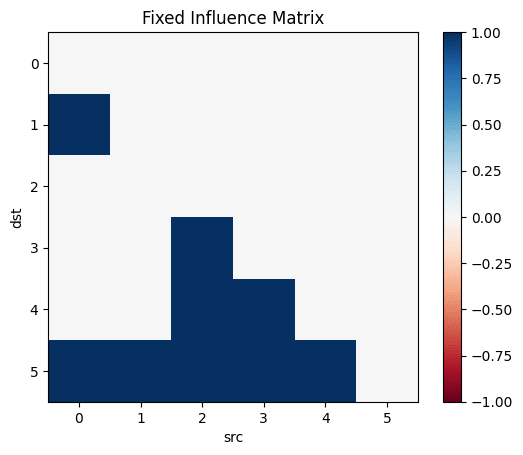
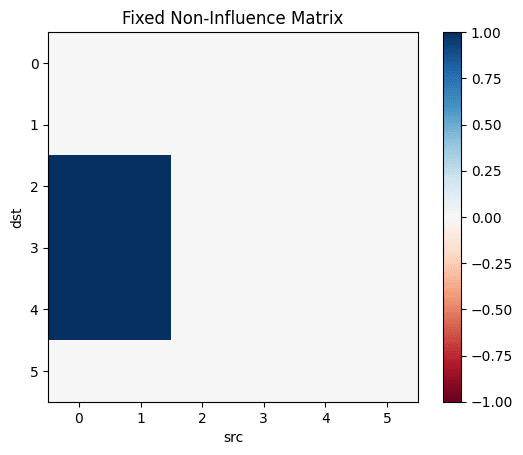
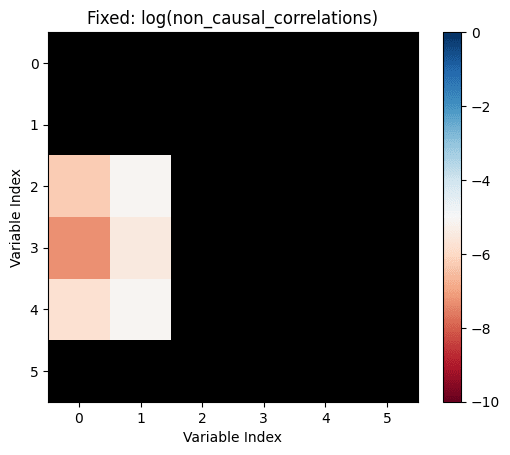
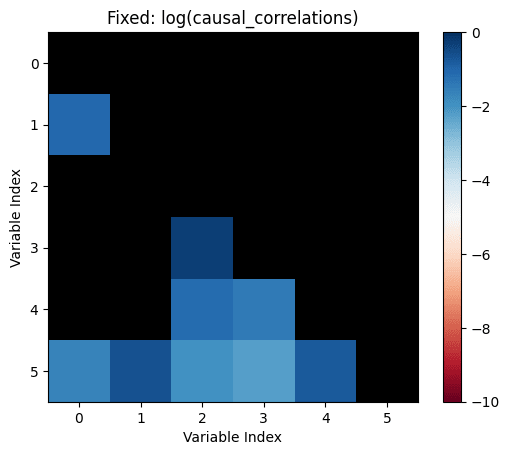
I don't believe that the generating process for your simulation resembles that in the real world. If it doesn't, I don't see the value in such a simulation.
For an analysis of some situations where unmeasurably small correlations are associated with strong causal influences and high correlations (±0.99) are associated with the absence of direct causal links, see my paper "When causation does not imply correlation: robust violations of the Faithfulness axiom" (arXiv, in book). The situations where this happens are whenever control systems are present, and they are always present in biological and social systems.
Here are three further examples of how to get non-causal correlations and causal non-correlations. They all result from taking correlations between time series. People who work with time series data generally know about these pitfalls, but people who don't may not be aware of how easy it is to see mirages.
The first is the case of a bounded function and its integral. These have zero correlation with each other in any interval in which either of the two takes the same value at the beginning and the end. (The proof is simple and can be found in the paper of mine I cited.) For example, this is the relation between the current through a capacitor and the voltage across it. Set up a circuit in which you can turn a knob to change the voltage, and you will see the current vary according to how you twiddle the knob. Voltage is causing current. Set up a different circuit where a knob sets the current and you can use the current to cause the voltage. Over any interval in which the operating knob begins and ends in the same position, the correlation will be zero. People who deal with time series have techniques for detecting and removing integrations from the data.
The second is the correlation between two time series that both show a trend over time. This can produce arbitrarily high correlations between things that have nothing to do with each other, and therefore such a trend is not evidence of causation, even if you have a story to tell about how the two things are related. You always have to detrend the data first.
The third is the curious fact that if you take two independent paths of a Wiener process (one-dimensional Brownian motion), then no matter how frequently you sample them over however long a period of time, the distribution of the correlation coefficient remains very broad. Its expected value is zero, because the processes are independent and trend-free, but the autocorrelation of Brownian motion drastically reduces the effective sample size to about 5.5. Yes, even if you take a million samples from the two paths, it doesn't help. The paths themselves, never mind sampling from them, can have high correlation, easily as extreme as ±0.8. The phenomenon was noted in 1926, and a mathematical treatment given in "Yule's 'Nonsense Correlation' Solved!" (arXiv, journal). The figure of 5.5 comes from my own simulation of the process.
Modus ponens, modus tollens: I am interested in that question, and the answer (for questions considered worth asking to forecasters) is ~40%.
But having a better selection of causal graphs than just "uniformly" would be good. I don't know how to approach that, though—is the world denser or sparser than what I chose?