Google DeepMind reports on a system for solving mathematical problems that allegedly is able to give complete solutions to four of the six problems on the 2024 IMO, putting it near the top of the silver-medal category.
Well, actually, two systems for solving mathematical problems: AlphaProof, which is more general-purpose, and AlphaGeometry, which is specifically for geometry problems. (This is AlphaGeometry 2; they reported earlier this year on a previous version of AlphaGeometry.)
AlphaProof works in the "obvious" way: an LLM generates candidate next steps which are checked using a formal proof-checking system, in this case Lean. One not-so-obvious thing, though: "The training loop was also applied during the contest, reinforcing proofs of self-generated variations of the contest problems until a full solution could be found."
[EDITED to add:] Or maybe it doesn't work in the "obvious" way. As cubefox points out in the comments below, DeepMind's description doesn't explicitly say that it does that, and they're infuriatingly vague about how "AlphaProof generates solution candidates". The previous paragraph at least insinuates that it does it with an LLM, but it's very unclear.
(That last bit is reminiscent of something from the world of computer go: a couple of years ago someone trained a custom version of KataGo specifically to solve the infamous Igo Hatsuyoron problem 120, starting with ordinary KataGo and feeding it training data containing positions reachable from the problem's starting position. They claim to have laid that problem to rest at last.)
AlphaGeometry is similar but uses something specialized for (I think) Euclidean planar geometry problems in place of Lean. The previous version of AlphaGeometry allegedly already performed at gold-medal IMO standard; they don't say anything about whether that version was already able to solve the 2024 IMO problem that was solved using AlphaGeometry 2.
AlphaProof was able to solve questions 1, 2, and 6 on this year's IMO (two algebra, one number theory). It produces Lean-formalized proofs. AlphaGeometry 2 was able to solve question 4 (plane geometry). It produces proofs in its own notation.
The solutions found by the Alpha... systems are at https://storage.googleapis.com/deepmind-media/DeepMind.com/Blog/imo-2024-solutions/index.html. (There are links in the top-of-page navbar to solutions to the individual problems.)
(If you're curious about the IMO questions or want to try them yourself before looking at the machine-generated proofs, you can find them -- and those for previous years -- at https://www.imo-official.org/problems.aspx.)
One caveat (note: an earlier version of what I wrote failed to notice this and quite wrongly explicitly claimed something different): "First, the problems were manually translated into formal mathematical language for our systems to understand." It feels to me like it shouldn't be so hard to teach an LLM to convert IMO problems into Lean or whatever, but apparently they aren't doing that yet. [EDITED to add:] But it seems they are doing this to generate training data. Perhaps the fact that they didn't do it for the IMO problem statements themselves reveals something about the limitations of their English-to-Lean translator?
Another caveat: "Our systems solved one problem within minutes and took up to three days to solve the others." Later on they say that AlphaGeometry 2 solved the geometry question within 19 seconds, so I guess that was also the one that was done "within minutes". Three days is a lot longer than human IMO contestants get given, but this feels to me like the sort of thing that will predictably improve pretty rapidly.
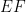 (USAJMO 2014/6). Not knowing either of these makes it more difficult to solve the problem synthetically in the time limit. As a reference,
(USAJMO 2014/6). Not knowing either of these makes it more difficult to solve the problem synthetically in the time limit. As a reference,
The news is not very old yet. Lots of potential for people to start freaking out.