Comment Permalink

[comment deleted]1mo-13-1

Deleted by lillybaeum, 05/04/2025

Reason: This was stupid.

See in context

89 $500 Bounty Problem: Are (Approximately) Deterministic Natural Latents All You Need?

by johnswentworth, David Lorell

21st Apr 2025

4 min read

89

Our posts on natural latents have involved two distinct definitions, which we call "stochastic" and "deterministic" natural latents. We conjecture that, whenever there exists a stochastic natural latent (to within some approximation), there also exists a deterministic natural latent (to within a comparable approximation). We are offering a $500 bounty to prove this conjecture.

Some Intuition From The Exact Case

In the exact case, in order for a natural latent to exist over random variables , the distribution has to look roughly like this:

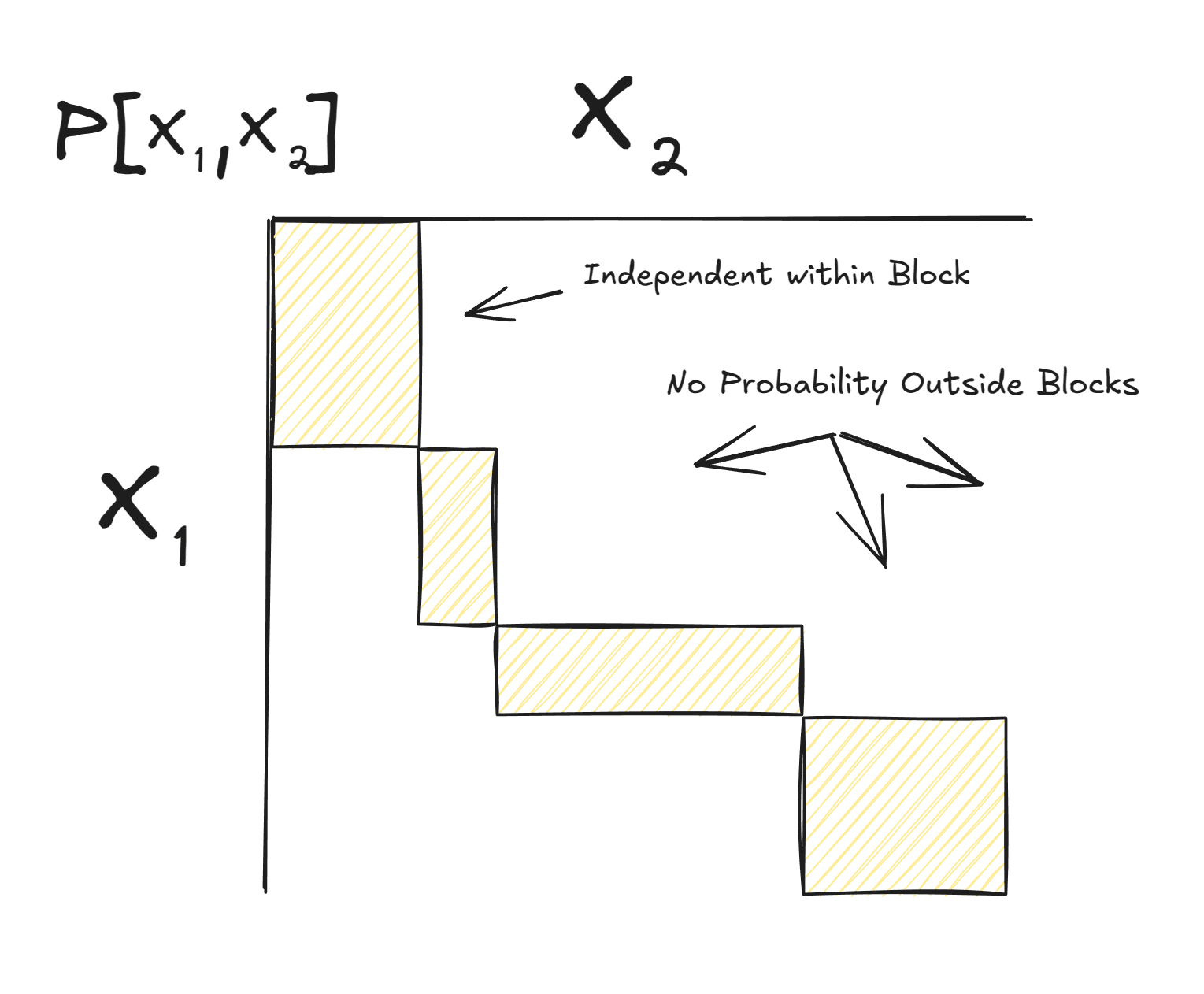
Each value of $X_{1}$ and each value of $X_{2}$ occurs in only one "block", and within the "blocks", $X_{1}$ and $X_{2}$ are independent. In that case, we can take the (exact) natural latent to be a block label.

Notably, that block label is a deterministic function of X.

However, we can also construct other natural latents for this system: we simply append some independent random noise to the block label. That natural latent is not a deterministic function of X; it's a "stochastic" natural latent.

In the exact case, if a stochastic natural latent exists, then the distribution must have the form pictured above, and therefore the block label is a deterministic natural latent. In other words: in the exact case, if a stochastic natural latent exists, then a deterministic natural latent also exists. The goal of the $500 bounty is to prove that this still holds in the approximate case.

Approximation Adds Qualitatively New Behavior

If you want to tackle the bounty problem, you should probably consider a distribution like this:

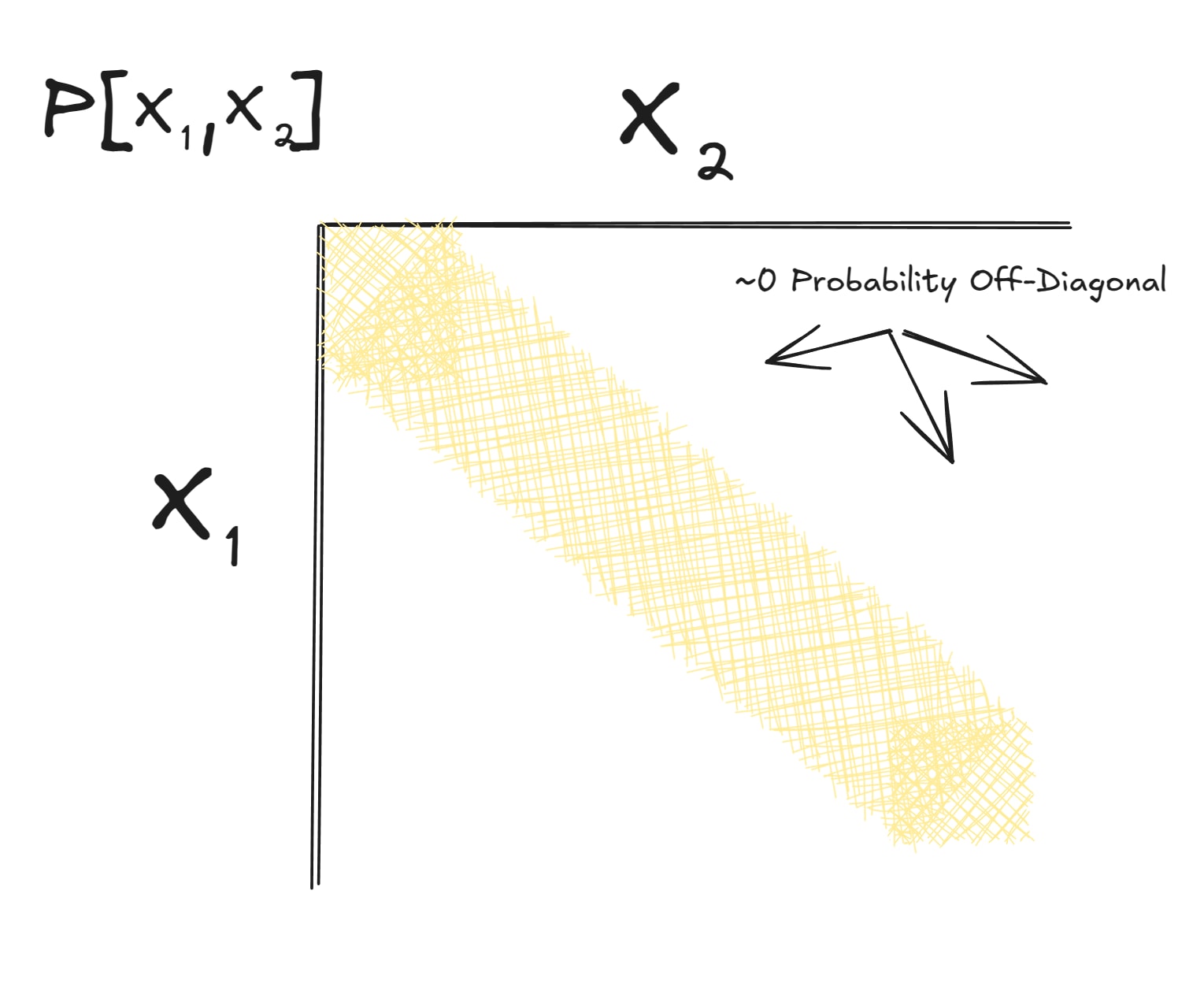
Distributions like this can have approximate natural latents, while being qualitatively different from the exact picture. A concrete example is the biased die: $X_{1}$ and $X_{2}$ are each 500 rolls of a biased die of unknown bias (with some reasonable prior on the bias). The bias itself will typically be an approximate stochastic natural latent, but the lower-order bits of the bias are not approximately deterministic given X (i.e. they have high entropy given X).

The Problem

"Stochastic" Natural Latents

Stochastic natural latents were introduced in the original Natural Latents post. Any latent $Λ$ over random variables $X_{1}, X_{2}$ is defined to be a stochastic natural latent when it satisfies these diagrams:

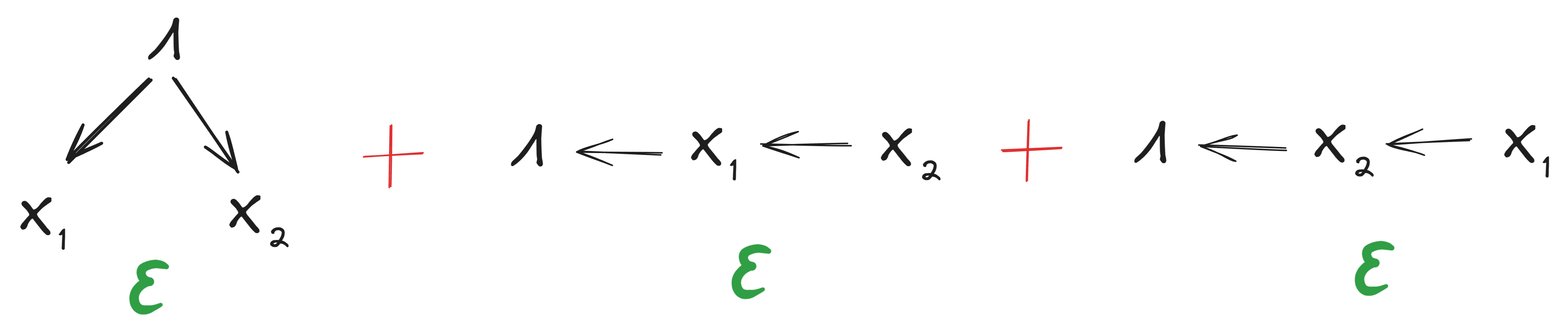
... and $Λ$ is an approximate stochastic natural latent (with error $ϵ$ ) when it satisfies the approximate versions of those diagrams to within $ϵ$ , i.e.

$ϵ \geq D_{K L} (P [X, Λ] | | P [Λ] P [X_{1} | Λ] P [X_{2} | Λ])$

$ϵ \geq D_{K L} (P [X, Λ] | | P [X_{2}] P [X_{1} | X_{2}] P [Λ | X_{1}])$

$ϵ \geq D_{K L} (P [X, Λ] | | P [X_{1}] P [X_{2} | X_{1}] P [Λ | X_{2}])$

Key thing to note: if $Λ$ satisfies these conditions, then we can create another stochastic natural latent $Λ^{'}$ by simply appending some random noise to $Λ$ , independent of $X$ . This shows that $Λ$ can, in general, contain arbitrary amounts of irrelevant noise while still satisfying the stochastic natural latent conditions.

"Deterministic" Natural Latents

Deterministic natural latents were introduced in a post by the same name. Any latent $Λ$ over random variables $X_{1}, X_{2}$ is defined to be a deterministic natural latent when it satisfies these diagrams:

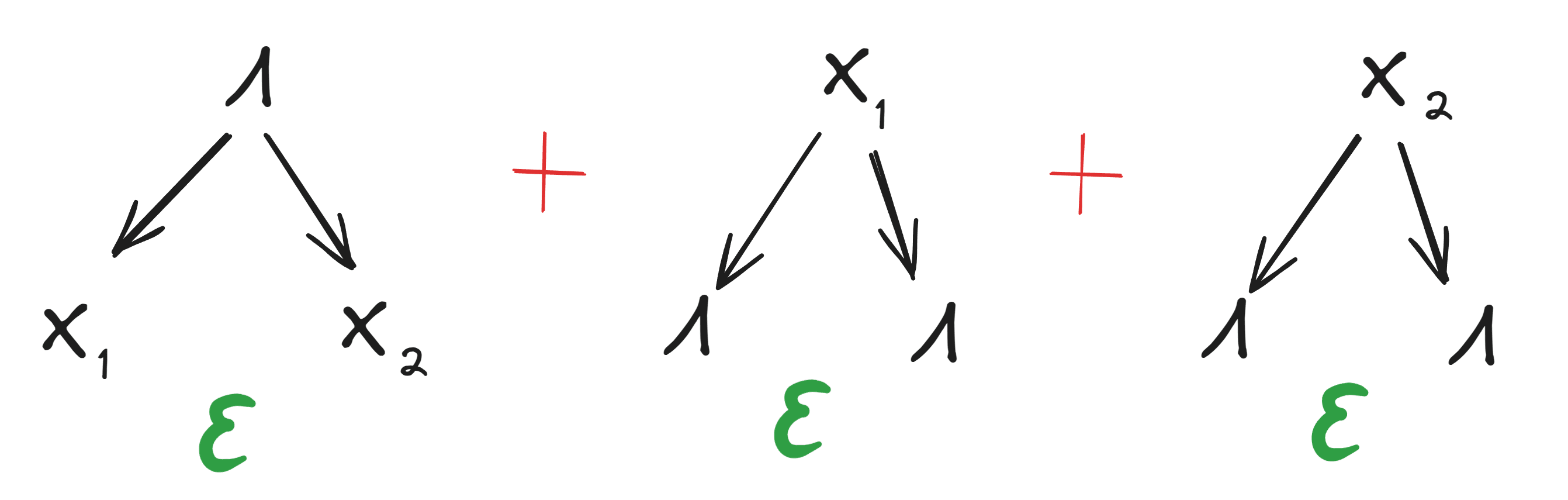
... and $Λ$ is an approximate deterministic natural latent (with error $ϵ$ ) when it satisfies the approximate versions of those diagrams to within $ϵ$ , i.e.

$ϵ \geq D_{K L} (P [X, Λ] | | P [Λ] P [X_{1} | Λ] P [X_{2} | Λ])$

$ϵ \geq H (Λ | X_{1})$

$ϵ \geq H (Λ | X_{2})$

See the linked post for explanation of a variable appearing multiple times in a diagram, and how the approximation conditions for those diagrams simplify to entropy bounds.

Note that the deterministic natural latent conditions, either with or without approximation, imply the stochastic natural latent conditions; a deterministic natural latent is also a stochastic natural latent.

Also note that one can instead define an approximate deterministic natural latent via just one diagram, and this is also a fine starting point for purposes of this bounty:

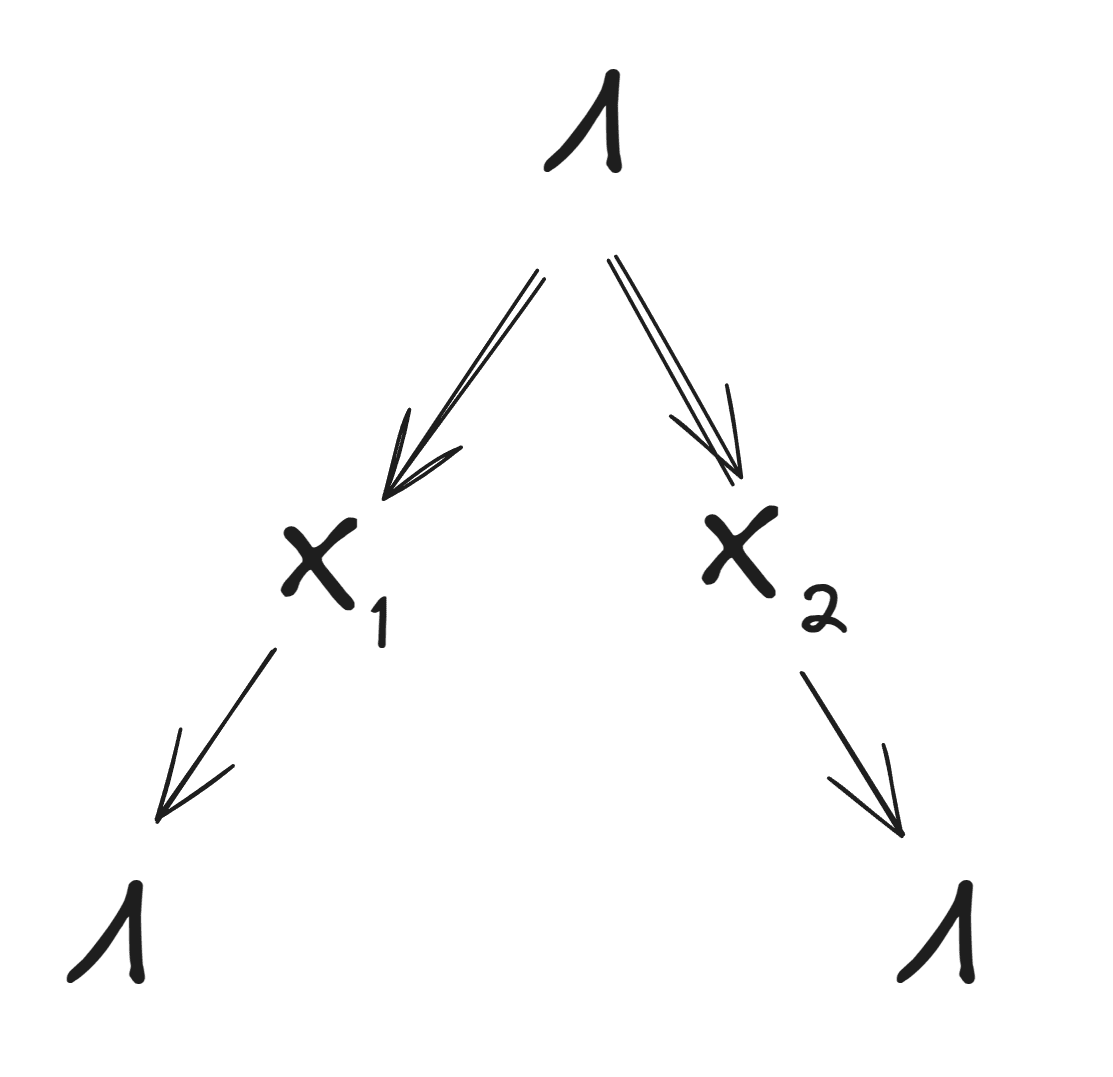
What We Want For The Bounty

We'd like a proof that, if a stochastic natural latent exists over two variables $X_{1}, X_{2}$ to within approximation $ϵ$ , then a deterministic natural latent exists over those two variables to within approximation roughly $ϵ$ . When we say "roughly", e.g. $2 ϵ$ or $3 ϵ$ would be fine; it may be a judgement call on our part if the bound is much larger than that.

We're probably not interested in bounds which don't scale to zero as $ϵ$ goes to zero, though we could maybe make an exception if e.g. there's some way of amortizing costs across many systems such that costs go to zero-per-system in aggregate (though we don't expect the problem to require those sorts of tricks).

Bounds should be global, i.e. apply even when $ϵ$ is large. We're not interested in e.g. first or second order approximations for small $ϵ$ unless they provably apply globally.

We might also award some fraction of the bounty for a counterexample. That would be much more of a judgement call, depending on how thoroughly the counterexample kills hope of any conjecture vaguely along these lines.

In terms of rigor and allowable assumptions, roughly the level of rigor and assumptions in the posts linked above is fine.

Why We Want This

Deterministic natural latents are a lot cleaner both conceptually and mathematically than stochastic natural latents. Alas, they're less general... unless this conjecture turns out to be true, in which case they're not less general. That sure would be nice.

Bounties & Prizes (active)AI

Frontpage

89

Mentioned in

72$500 + $500 Bounty Problem: Does An (Approximately) Deterministic Maximal Redund Always Exist?

$500 Bounty Problem: Are (Approximately) Deterministic Natural Latents All You Need?

New Comment

17 comments, sorted by

top scoring

Click to highlight new comments since: Today at 1:59 AM

[-]Alfred Harwood1mo230

This seems like an interesting problem! I've been thinking about it a little bit but wanted to make sure I understood before diving in too deep. Can I see if I understand this by going through the biased coin example?

Suppose I have 2^5 coins and each one is given a unique 5-bit string label covering all binary strings from 00000 to 11111. Call the string on the label .

The label given to the coin indicates its 'true' bias. The string 00000 indicates that the coin with that label has p(heads)=0. The coin labelled 11111 has p(heads)=1. The ‘true’ p(heads) increases in equal steps going up from 00000 to 00001 to 00010 etc. Suppose I randomly pick a coin from this collection, toss it 200 times and call the number of heads X_1. Then I toss it another 200 times and call the number of heads X_2.

Now, if I tell you what the label on the coin was (which tells us the true bias of the coin), telling you X_1 would not give you any more information to help you guess X_2 (and vice versa). This is the first Natural Latent condition ( $Λ$ induces independence between X_1 and X_2). Alternatively, if I didn’t tell you the label, you could estimate it from either X_1 or X_2 equally well. This is the other two diagrams.

I think that the full label $Λ$ will be an approximate stochastic natural latent. But if we consider only the first bit^[1] of the label (which roughly tells us whether the bias is above or below 50% heads) then this bit will be a deterministic natural latent because with reasonably high certainty, you can guess the first bit of $Λ$ from X_1 or X_2. This is because the conditional entropy H(first bit of $Λ$ |X_1) is low. On the other hand H( $Λ$ | X_1) will be high. If I get only 23 heads out of 200 tosses, I can be reasonably certain that the first bit of $Λ$ is a 0 (ie the coin has a less than 50% of coming up heads) but can't be as certain what the last bit of $Λ$ is. Just because $Λ$ satisfies the Natural Latent conditions within $ϵ$ , this doesn’t imply that $Λ$ satisfies $H (Λ | X_{1}) < ϵ$ . We can use X_1 to find a 5-bit estimate of $Λ$ , but most of the useful information in that estimate is contained in the first bit. The second bit might be somewhat useful, but its less certain than the first. The last bit of the estimate will largely be noise. This means that going from using $Λ$ to using ‘first bit of $Λ$ ’ doesn’t decrease the usefulness of the latent very much, since the stuff we are throwing out is largely random. As a result, the ‘first bit of $Λ$ ’ will still satisfy the natural latent conditions almost as well as $Λ$ . By throwing out the later bits, we threw away the most 'stochastic' bits, while keeping the most 'latenty' bits.

So in this case, we have started from a stochastic natural latent and used it to construct a deterministic natural latent which is almost as good. I haven’t done the calculation, but hopefully we could say something like ‘if $Λ$ satisfies the natural latent conditions within $ϵ$ then the first bit of $Λ$ satisfies the natural latent conditions within $2 ϵ$ (or $3 ϵ$ or something else)’. Would an explicit proof of a statement like this for this case be a special case of the general problem?

The problem question could be framed as something like: “Is there some standard process we can do for every stochastic natural latent, in order to obtain a deterministic natural latent which is almost as good (in terms of \epsilon)”. This process will be analogous to the ‘throwing away the less useful/more random bits of \lambda’ which we did in the example above. Does this sound right?

Also, can all stochastic natural latents can be thought of as 'more approximate' deterministic latents? If a latent satisfies the the three natural latents conditions within $ϵ_{1}$ , we can always find a (potentially much bigger) $ϵ_{2}$ such that this latent also satisfies the deterministic latent condition, right? This is why you need to specify that the problem is showing that a deterministic natural latent exists with 'almost the same' $ϵ$ . Does this sound right?

^{^}
I'm going to talk about the 'first bit' but an equivalent argument might also hold for the 'first two bits' or something. I haven't actually checked the maths.

[-]johnswentworth1mo50

Some details mildly off, but I think you've got the big picture basically right.

Alternatively, if I didn’t tell you the label, you could estimate it from either X_1 or X_2 equally well. This is the other two diagrams.

Minor clarification here: the other two diagrams say not only that I can estimate the label equally well from either or $X_{2}$ , but that I can estimate the label (approximately) equally well from $X_{1}$ , $X_{2}$ , or the pair $(X_{1}, X_{2})$ .

I think that the full label $Λ$ will be an approximate stochastic natural latent.

I'd have to run the numbers to check that 200 flips is enough to give a high-confidence estimate of $Λ$ (in which case 400 flips from the pair of variables will also put high confidence on the same value with high probability), but I think yes.

But if we consider only the first bit^[1] of the label (which roughly tells us whether the bias is above or below 50% heads) then this bit will be a deterministic natural latent because with reasonably high certainty, you can guess the first bit of $Λ$ from $X_{1}$ or $X_{2}$ .

Not quite; I added some emphasis. The first bit will (approximately) satisfy the two redundancy conditions, i.e. $X_{1} \to X_{2} \to 1bit (Λ)$ and $X_{2} \to X_{1} \to 1bit (Λ)$ , and indeed will be an approximately deterministic function of $X$ . But it won't (approximately) satisfy the mediation condition $X_{1} \leftarrow 1bit (Λ) \to X_{2}$ ; the two sets of flips will not be (approximately) independent given only the first bit. (At least not to nearly as good an approximation as the original label.)

That said, the rest of your qualitative reasoning is correct. As we throw out more low-order bits, the mediation condition becomes less well approximated, the redundancy conditions become better approximated, and the entropy of the coarse-grained latent given $X$ falls.

So to build a proof along these lines, one would need to show that a bit-cutoff can be chosen such that bit_cutoff( $Λ$ ) still mediates (to an approximation roughly $ϵ$ -ish), while making the entropy of bit_cutoff( $Λ$ ) low given $X$ .

I do think this is a good angle of attack on the problem, and it's one of the main angles I'd try.

If a latent satisfies the the three natural latents conditions within $ϵ_{1}$ , we can always find a (potentially much bigger) $ϵ_{2}$ such that this latent also satisfies the deterministic latent condition, right? This is why you need to specify that the problem is showing that a deterministic natural latent exists with 'almost the same' $ϵ$ . Does this sound right?

Yes. Indeed, if we allow large enough $ϵ$ (possibly scaling with system size/entropy) then there's always a deterministic natural latent regardless; the whole thing becomes trivial.

[-]Donald Hobson14d40

I'd have to run the numbers to check that 200 flips is enough to give a high-confidence estimate of

It isn't enough. See plot. Also, 200 not being enough flips is part of what makes this interesting. With a million flips, this would pretty much just be the exact case. The fact that it's only 200 flips gives you a tradeoff in how many label_bits to include.

[-]Alfred Harwood1mo40

Thanks for the clarifications, that all makes sense. I will keep thinking about this!

[-]Donald Hobson14d40

Here is the probability density function for heads plotted for each of your coins.

python code

import numpy as np
l=np.linspace(0,1,32)
def f(a):
a=np.array([a,1-a])
b=a
for i in range(199):
b=np.convolve(b,a)
return b

q=np.arange(201)
import matplotlib.pyplot as plt
ff=[f(i) for i in l]
plt.plot(ff);plt.show()

for i in ff:
_=plt.plot(q,i)

plt.show()
plt.xlabel("heads")
Text(0.5, 0, 'heads')
plt.ylabel("prob")
Text(0, 0.5, 'prob')
for i in ff:
_=plt.plot(q,i)

plt.show()

[-]David Johnston1mo50

I've thought about it a bit, I have a line of attack for a proof, but there's too much work involved in following it through to an actual proof so I'm going to leave it here in case it helps anyone.

I'm assuming everything is discrete so I can work with regular Shannon entropy.

Consider the range of the function $g_{1} : λ \mapsto P (X_{1} | Λ = λ)$ and $R_{2}$ defined similarly. Discretize $R_{1}$ and $R_{2}$ (chop them up into little balls). Not sure which metric to use, maybe TV.

Define $Λ_{1}^{'} (λ)$ to be the index of the ball into which $P (X_{1} | Λ = λ)$ falls, $Λ_{2}^{'}$ similar. So if $d (P (X_{1} | Λ = a), P (X_{1} | Λ = b))$ is sufficiently small, then $Λ_{1}^{'} (a) = Λ_{1}^{'} (b)$ .

By the data processing inequality, conditions 2 and 3 still hold for $Λ^{'} = (Λ_{1}^{'}, Λ_{2}^{'})$ . Condition 1 should hold with some extra slack depending on the coarseness of the discretization.

It takes a few steps, but I think you might be able to argue that, with high probability, for each $X_{2} = x_{2}$ , the random variable $Q_{1} := P (X_{1} | Λ_{1}^{'})$ will be highly concentrated (n.b. I've only worked it through fully in the exact case, and I think it can be translated to the approximate case but I haven't checked). We then invoke the discretization to argue that $H (Λ_{1}^{'} | X_{1})$ is bounded. The intuition is that the discretization forces nearby probabilities to coincide, so if $Q_{1}$ is concentrated then it actually has to "collapse" most of its mass onto a few discrete values.

We can then make a similar argument switching the indices to get $H (Λ_{2}^{'} | X_{2})$ bounded. Finally, maybe applying conditions 2 and 3 we can get $H (Λ_{1}^{'} | X_{2})$ bounded as well, which then gives a bound on $H (Λ | X_{i})$ .

I did try feeding this to Gemini but it wasn't able to produce a proof.

[-]J Bostock1mo70

I've been working on the reverse direction: chopping up by clustering the points (treating each distribution as a point in distribution space) given by $P [Λ | X = x]$ , optimizing for a deterministic-in- $X$ latent $Δ = Δ (X)$ which minimizes $D_{K L} (P [Λ | X] | | P [Λ | Δ (X)])$ .

This definitely separates $X_{1}$ and $X_{2}$ to some small error, since we can just use $Δ$ to build a distribution over $Λ$ which should approximately separate $X_{1}$ and $X_{2}$ .

To show that it's deterministic in $X_{1}$ (and by symmetry $X_{2}$ ) to some small error, I was hoping to use the fact that---given $X_{1}$ --- $X_{2}$ has very little information about $Λ$ , so it's unlikely that $P [Λ | X_{1}]$ is in a different cluster to $P [Λ | X_{1}, X_{2}]$ . This means that $P [Δ | X_{1}]$ would just put most of the weight on the cluster containing $P [Λ | X_{1}]$ .

A constructive approach for $Δ$ would be marginally more useful in the long-run, but it's also probably easier to prove things about the optimal $Δ$ . It's also probably easier to prove things about $Δ$ for a given number of clusters $| Δ |$ , but then you also have to prove things about what the optimal value of $| Δ |$ is.

[-]johnswentworth1mo70

Sounds like you've correctly understood the problem and are thinking along roughly the right lines. I expect a deterministic function of won't work, though.

Hand-wavily: the problem is that, if we take the latent to be a deterministic function $Δ (X)$ , then $P [X | Δ (X)]$ has lots of zeros in it - not approximate-zeros, but true zeros. That will tend to blow up the KL-divergences in the approximation conditions.

I'd recommend looking for a function $Δ (Λ)$ . Unfortunately that does mean that low entropy of $Δ (Λ)$ given $X$ has to be proven.

[-]J Bostock1mo40

Huh, I had vaguely considered that but I expected any terms to be counterbalanced by $P [X, Δ (X)] = 0$ terms, which together contribute nothing to the KL-divergence. I'll check my intuitions though.

I'm honestly pretty stumped at the moment. The simplest test case I've been using is for $X_{1}$ and $X_{2}$ to be two flips of a biased coin, where the bias is known to be either $k$ or $1 - k$ with equal probability of either. As $k$ varies, we want to swap from $Δ ≅ Λ$ to the trivial case $| Δ | = 1$ and back. This (optimally) happens at around $k = 0.08$ and $k = 0.92$ . If we swap there, then the sum of errors for the three diagrams of $Δ$ does remain less than $2 (ϵ + ϵ + ϵ)$ at all times.

Likewise, if we do try to define $Δ (X)$ , we need to swap from a $Δ$ which is equal to the number of heads, to $| Δ | = 1$ , and back.

In neither case can I find a construction of $Δ (X)$ or $Δ (Λ)$ which swaps from one phase to the other at the right time! My final thought is for $Δ$ to be some mapping $Λ \to P (Λ)$ consisting of a ball in probability space of variable radius (no idea how to calculate the radius) which would take $k \to {k}$ at $k \approx 1$ and $k \to {k, 1 - k}$ at $k \approx 0.5$ . Or maybe you have to map $Λ \to P (X)$ or something like that. But for now I don't even have a construction I can try to prove things for.

Perhaps a constructive approach isn't feasible, which probably means I don't have quite the right skillset to do this.

[-]J Bostock19d*40

OK so some further thoughts on this: suppose we instead just partition the values of directly by something like a clustering algorithm, based on $D_{K L}$ in $P [X | Λ]$ space, and take $Δ (Λ)$ just be the cluster that $λ$ is in:

Assuming we can do it with small clusters, we know that $P [X | Λ] \approx P [X | Δ]$ is pretty small, so $D_{K L} (P [X] | | P [X | Δ])$ is also small.

And if we consider $X_{2} \leftarrow X_{1} \to Λ$ , this tells us that learning $X_{1}$ restricts us to a pretty small region of $P [X_{2}]$ space (since $P [X_{2} | X_{1}] \approx P [X_{2} | X_{1}, Λ]$ ) so $Δ$ should be approximately deterministic in $X_{1}$ . This second part is more difficult to formalize, though.

Edit: The real issue is whether or not we could have lots of $Λ$ values which produce the same distribution over $X_{2}$ but different distributions over $X_{1}$ , and all be pretty likely given $X_{1} = x_{1}$ for some $x_{1}$ . I think this just can't really happen for probable values of $x_{1}$ , because if these values of $λ$ produce the same distribution over $X_{2}$ , but different distributions over $X_{1}$ , then that doesn't satisfy $X_{1} \leftarrow X_{2} \to Λ$ , and secondly because if they produced wildly different distributions over $X_{1}$ , then that means they can't all have high values of $P [X_{1} = x_{1} | Λ = λ]$ , and so they're not gonna have high values of $P [Λ = λ | X_{1} = x_{1}]$ .

[-]johnswentworth15d*40

Here's a trick which might be helpful for anybody tackling the problem.

First, note that is always a sufficient statistic of $Λ$ for $X$ , i.e.

$Λ \to f (Λ) \to X$

Now, we typically expect that the lower-order bits of $f (Λ)$ are less relevant/useful/interesting. So, we might hope that we can do some precision cutoff on $f (Λ)$ , and end up with an approximate suficient statistic, while potentially reducing the entropy (or some other information content measure) of $f (Λ)$ a bunch. We'd broadcast the cutoff function like this:

$g (Λ) := precison_cutoff (f (Λ)) = (x \mapsto precision_cutoff (P [X = x | Λ]))$

Now we'll show a trick for deriving $D_{K L}$ bounds involving $g (Λ)$ .

First note that

$E [D_{K L} (P [X | Λ] | | P [X | g (Λ)])] \leq E [D_{K L} (P [X | Λ] | | g (Λ))]$

This is a tricky expression, so let's talk it through. On the left, $g (Λ)$ is treated informationally; it's just a generic random variable constructed as a generic function of $Λ$ , and we condition on that random variable in the usual way. On the right, the output-value of $g$ is being used as a distribution over $X$ .

The reason this inequality holds is because a Bayes update is the "best" update one can make, as measured by expected $D_{K L}$ . Specifically, if I'm given the value of any function $g (Λ)$ , then the distribution $Q$ (as a function of $g (Λ))$ which minimizes $E [D_{K L} (P [X | Λ] | | Q)]$ is $P [X | g (Λ)]$ . Since $P [X | g (Λ)]$ minimizes that expected $D_{K L}$ , any other distribution over $X$ (as a function of $g (Λ)$ ) can only do "worse" - including $g (Λ)$ itself, since that's a distribution over $X$ , and is a function of $g (Λ)$ .

Plugging in the definition of $g$ , that establishes

$E [D_{K L} (P [X | Λ] | | P [X | g (Λ)])] \leq E [D_{K L} (P [X | Λ] | | (x \mapsto precision_cutoff (P [X = x | Λ])))]$

Then the final step is to use the properties of whatever $precision_cutoff$ function one chose, to establish that $E [D_{K L} (P [X | Λ] | | (x \mapsto precision_cutoff (P [X = x | Λ])))]$ can't be too far from $E [D_{K L} (P [X | Λ] | | P [X | Λ])]$ , i.e. 0. That produces an upper bound on $E [D_{K L} (P [X | Λ] | | P [X | g (Λ)])]$ , where the bound is 0 + (whatever terms came from the precision cutoff).

[-]johnswentworth15d20

@Alfred Harwood @David Johnston

If anyone else would like to be tagged in comments like this one on this post, please eyeball-react on this comment. Alfred and David, if you would like to not be tagged in the future, please say so.

[-]David Johnston1mo*10

Your natural latents seem to be quite related to the common construction IID variables conditional on a latent - in fact, all of your examples are IID variables (or "bundles" of IID variables) conditional on that latent. Can you give me an interesting example of a natural latent that is not basically the conditionally IID case?

(I was wondering if the extensive literature on the correspondence between De Finetti type symmetries and conditional IID representations is of any help to your problem. I'm not entirely sure if it is, given that mostly addresses the issue of getting from a symmetry to a conditional independence, whereas you want to get from one conditional independence to another, but it's plausible some of the methods are applicable)

[-]johnswentworth1mo20

A natural latent is, by definition, a latent which satisfies two properties. The first is that the observables are IID conditional on the latent, i.e. the common construction you're talking about. That property by itself doesn't buy us much of interest, for our purposes, but in combination with the other property required for a natural latent, it buys quite a lot.

[-]David Johnston1mo65

Wait, I thought the first property was just independence, not also identically distributed.

In principle I could have e.g. two biased coins with their biases different but deterministically dependent.

[-]johnswentworth1mo40

Oh, you're right. Man, I was really not paying attention before bed last night! Apologies, you deserve somewhat less tired-brain responses than that.

[+][comment deleted]1mo-13-1

Deleted by lillybaeum, 05/04/2025

Reason: This was stupid.

Moderation Log