3 Answers sorted by
93
There are many articles on quantum cellular automata. See for example "A review of Quantum Cellular Automata", or "Quantum Cellular Automata, Tensor Networks, and Area Laws".
I think compared to the literature you're using an overly restrictive and nonstandard definition of quantum cellular automata. Specifically, it only makes sense to me to write as a product of operators like you have if all of the terms are on spatially disjoint regions.
Consider defining quantum cellular automata instead as local quantum circuits composed of identical two-site unitary operators everywhere:
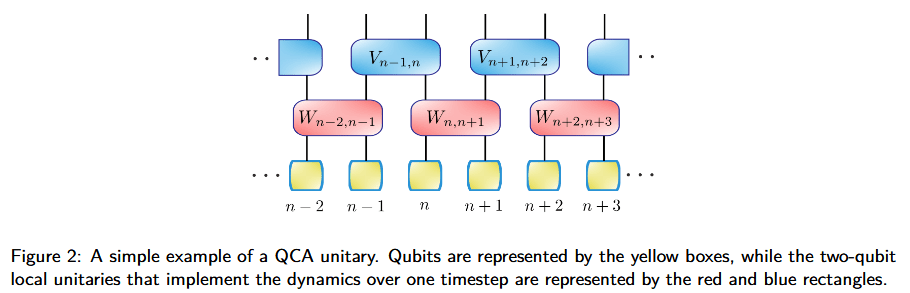
If you define them like this, then basically any kind of energy and momentum conserving local quantum dynamics can be discretized into a quantum cellular automata, because any two-site time and space independent quantum Hamiltonian can be decomposed into steps with identical unitaries like this using the Suzuki-Trotter decomposition.
I think compared to the literature you're using an overly restrictive and nonstandard definition of quantum cellular automata.
That makes sense! I'm searching for the simplest cellular-automaton-like thing that's still interesting to study. I may have gone too far in the "simple" direction; but I'd like to understand why this highly-restricted subset of QCAs is too simple.
Specifically, it only makes sense to me to write as a product of operators like you have if all of the terms are on spatially disjoint regions.
Hmm! That's not obvious to me; if there...
*
50I think you're looking for the irreducible representations of (edit: for 1D, ). I'll come back and explain this later, but it's going to take awhile to write up.
I've never been familiar enough with group-theory stuff to memorize the names (which, warning, also might mean that it will take you a lot of time to write a sufficiently-dumbed-down version), but the internet suggests is related to... the Minkowski metric? I would be flabbergasted to learn that something so specific-to-our-universe was relevant to this toy mathematical contraption.
*
30I think the basic reason that it's hard to make an interesting QCA using this definition is that it's hard to make a reversible CA. Reversible cellular automata are typically made using block-partitioning or a second-order method. The (classical) laws of physics also seem to have a flavor more similar to these than a GoL-style CA, in that they have independent position and velocity coordinates which each determine the time evolution of the other.
You know elementary cellular automata, where each of the boolean-valued cells evolves according to
x(k)t+1=f(x(k−1)t,x(k)t,x(k+1)t)where f:{0,1}3→{0,1}.
I think the natural quantum-mechanical extension of this is:
- there are 2(N := tape size) basis states: |00⋯00⟩ through |11⋯11⟩
- its time-evolution is given, of course, by a unitary operator U, which, expressed in that basis, is:
⟨y|U|x⟩=∏kf(x(k−1),x(k),x(k+1),y(k))You can take any elementary cellular automaton and quantum-ize it: just choose fquantum(a,b,c,z)=( if fclassical(a,b,c)=z then 1 else 0 ); then that product is 1 exactly when y is the classical evolution of x. (Not every fclassical gives rise to a unitary U, though; only the reversible ones.)
But... are there other unitary operators of this form, which aren't basically equivalent to reversible classical CAs? I think not, disappointingly, but I'm not sure, and I don't understand why not.
Bounty: $100 if you make me feel like I have a significantly deeper understanding of why all quantum elementary CAs are basically equivalent to classical elementary CAs (or show me I'm wrong and there actually is interesting behavior here). Partial payouts for partial successes.
My current understanding (the thing you have to enhance or beat) is:
- Any choice of f is equivalent to a choice of eight complex two-vectors →λ000,⋯,→λ111, each describing roughly "how (0/1)ish the next state of a cell should be given its current neighborhood."
- For unitarity, we want ⟨Ux|Uy⟩=⟨x|y⟩ for all x,y. If you bang through some math, I think this inner product turns out to equal the product of all 64 possible inner products of the →λabc s, raised to various powers:
⟨Ux|Uy⟩=(→λ000⋅→λ111)N000,111⋯(→λ000⋅→λ111)N000,111...where N000,111 is the number of locations where the neighborhood on tape x is 000 and the neighborhood on tape y is 111. For x=y, we want this product to be 1; for x≠y, we want this product to be 0, meaning at least one of the inner products with a nonzero N must be zero.
(Sanity check: if x=y, then Nabc,abc=1 and all the other Ns are 0. The inner products raised to power 0 disappear; the remaining ones are →λabc⋅→λabc, which is 1 as long as the →λs are normalized, so we get ⟨Ux|Ux⟩=1 practically for free. Great.)