In recent months and years I have seen sober analyses of compute price-performance suggesting that the price-performance in computing (that is, the amount of calculations per second that you can buy for a dollar) has a doubling time of something like 2-3 years. I do not think these figures are good predictors of future expectations, and I wish to explain why.
Over the years I have often returned to Kurzweil's[1] plot of price-performance in the 20th century. I occasionally update the plot on my own and marvel that the trend has persisted essentially unabated since it was published, illustrating a continuous and consistent trend from 1900 through 2023. For your reference and for the sake of clarity I have taken the original plot and added one recent point, the AMD RX 7600 GPU, which boasts 21.4 TFLOP/s (single-precision) at a price point of $269.99 as of this week. Take my word for it that the plots between 1995 and 2023 remain essentially on-trend.
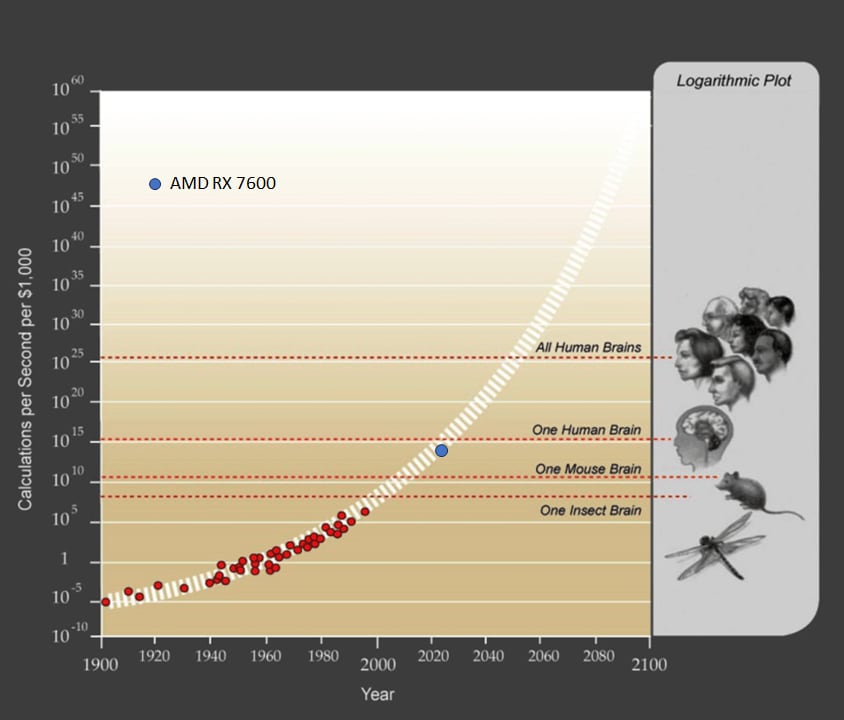
This plot[2] has no "doubling time" because it is super-exponential, i.e. there is an exponent inside the exponent, and the effective doubling time gets shorter over time. I have not found any published reference to how the white dashed band is calculated, but my own best fit line is:
where C is price-performance of compute in FLOP/s per $1000 and t in this case is years-since-1900. The instantaneous doubling time for this trend as of today would be about 0.93 years, less than half of even the most Pollyannaish of the recent forecasts. And the instantaneous doubling time obviously gets shorter each year.
The discrepancy between this <1 year doubling time and the >2 year doubling time observed in more recent publications is explained by the fact that trends calculated on the basis of narrow, recent time-frames will only capture one paradigm, e.g. the "GPU paradigm", which, like all individual paradigms in technology, exhibits S-curve behavior, starting out slow, accelerating, and then flattening. I also note that serious authors tend to present doubling-time figures that lean in the pessimistic direction.
Of course, it is entirely possible that 2023 marks the end of the validity of the above super-exponential trend. Perhaps, for some reason, no new computing paradigm arises to put us back on the white dashed band.
I feel it is important to consider that predictions for the end of the decade are wildly different depending on whether we extrapolate using this super-exponential trend or a "merely" exponential trend. Using an exponential extrapolation from today, we would expect compute to be roughly 10x cheaper per FLOP/s by 2030. Using the super-exponential extrapolation projects something closer to 1000x improvement in price-performance. Take these numbers as rough, since the extrapolations depend very much on the minutiae of how you do your curve fit. Regardless of the details, it is a difference of orders of magnitude.
I don't know how exactly we could achieve 1000x price-performance in 7 years, but responsible forecasting requires that we be open to the possibility of unforeseeable paradigm shifts, and I wouldn't want to bet against a curve that has held up for 123 years. If you had tried to make forecasts over the timescale of a decade using an exponential trend at any point over the last 100 years, you would have been consistently wrong by a margin that only increases with each decade. It seems particularly important that we avoid being wrong this decade.
Discussion in the comments prompted me to add this table of data to the original post, so that it would be more visible and provide a shared frame of reference:
| Hardware | Precision | TFLOPS | Price ($) | FLOPS/$1000 |
| Nvidia GeForce RTX 4090 | FP8 | 82.58 | $1,600 | 5.16E+13 |
| AMD RX 7600 | FP8 | 21.5 | $270 | 7.96E+13 |
| TPU v5e | INT8 | 393 | $4730* | 8.31E+13 |
| H100 | FP16 | 1979 | $30,603 | 6.47E+13 |
| H100 | FP8 | 3958 | $30,603 | 1.29E+14 |
*The price point of the TPU v5e is estimated based on a variety of sources, and adjusted based on my calculations from the hourly usage rates.
- ^
I can't figure out if Kurzweil was the one to originally publish this plot, but I know that the first place I saw it was in The Singularity is Near in 2005.
- ^
For reference, the "one human brain" estimate comes from FLOPS = 86 billion neurons×1000 synapses/neuron×200 Hz = 10^16 - 10^17 FLOPSa mode of estimation that I suspect Kurzweil would admit is tendentious.
A double exponential model seems very questionable. Is there any theoretical reason why you chose to fit your model with a double exponential? When fitting your model using a double exponential, did you take into consideration fundamental limits of computation? One cannot engineer transistors to be smaller than atoms, and we are approaching the limit to the size of transistors, so one should not expect very much of an increase in the performance of computational hardware. We can add more transistors to a chip by stacking layers (I don't know how this would be manufactured, but 3D space has a lot of room), but the important thing is efficiency, and one cannot make the transistors more efficient by stacking more layers. With more layers in 3D chips, most transistors will just be off most of the time, so 3D chips provide a limited improvement.
Landauer's principle states that to delete a bit of information in computing, one must spend at least k⋅T⋅ln(2) energy where k is Boltzmann's constant, T is the temperature, and ln(2)=0.693…. Here,k≈1.38⋅10−23J/K (Joules per Kelvin) which is not a lot of energy at room temperature. As the energy efficiency of computation approaches Landauer's limit, one runs into problems such as thermal noise. Realistically, one should expect to spend more than 100kT energy per bit deletion in order to overcome thermal noise (and this is ). If one tries to avoid Landauer's limit using reversible computation, then the process of computation becomes more complicated, so with reversible computation, one trades energy efficiency per bit operation with the number of operations computed, and the amount of space one uses in performing that computation. The progress in computational hardware capabilities will slow down as one progresses from classical computation to reversible computation. There are also ways of cutting the energy efficiency of deletion of information from 100kT per bit to something much closer to kTln(2), but they seem like a complicated engineering challenge.
The Margolus-Levitin theorem states that it takes h4E energy to go from a quantum state to an orthogonal quantum state (by flipping a bit, one transforms a state into an orthogonal state) where h is Planck's constant (h≈6.626⋅10−34J⋅S (Joules times seconds)) and E is the energy. There are other fundamental limits to the capabilities of computation.
As I remarked in other comments on this post, this is a plot of price-performance. The denominator is price, which can become cheap very fast. Potentially, as the demand for AI inference ramps up over the coming decade, the price of chips falls fast enough to drive this curve without chip speed growing nearly as fast. It is primarily an economic argument, not a purely technological argument.
For the purposes of forecasting, and understanding what the coming decade will look like, I think we care more about price-performance than raw chip speed. This is part... (read more)