There is a new paper by Liu et al. that claims to have understood the key mechanism underlying grokking (potentially even generalization more broadly).
They argue:
1. Grokking can be explained via the norm of the weights. They claim that there is a constant level of the weight norm that is optimal for generalization.
2. If there is an optimal level of the weight norm, the weight norm of your model after initialization can be either too low, too high or optimal. They claim that grokking is a phenomenon where we initialize the model with a large weight norm and it then slowly walks toward the optimal weight norm and then generalizes.
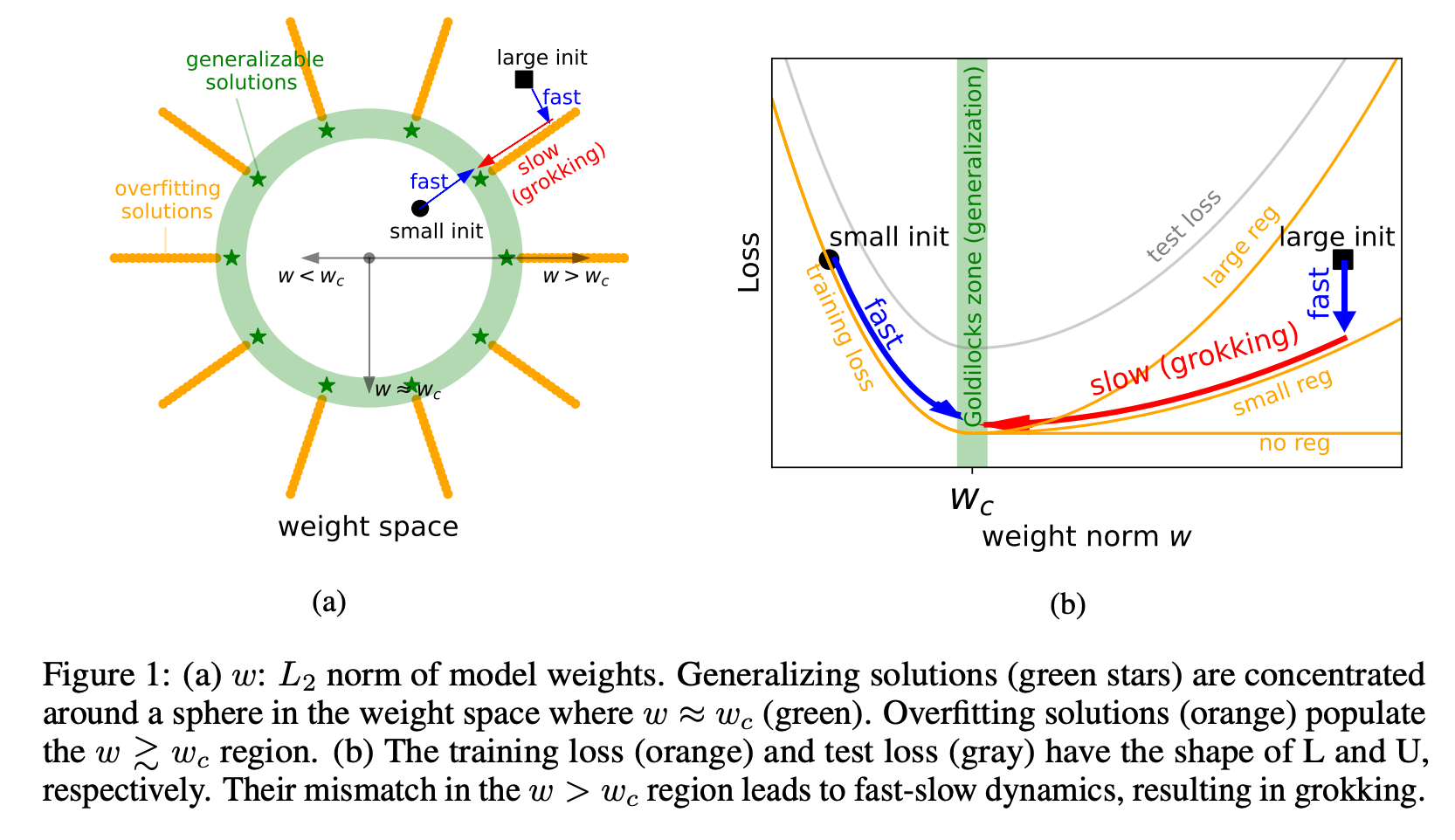
3. They also claim that you can get the same results as grokking but much faster if you set the weight norm correctly at every step.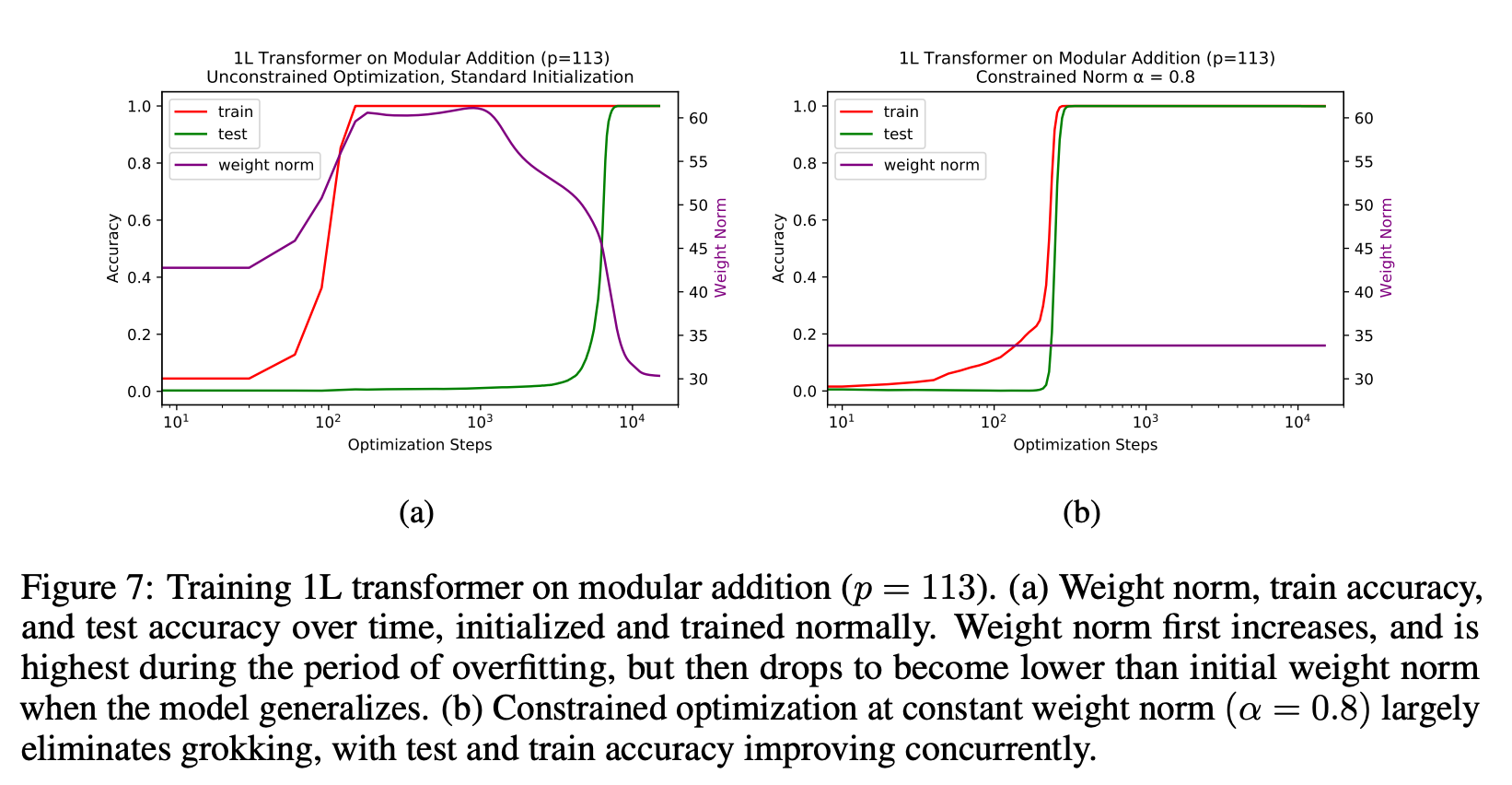
4. They set the norm "correctly" by rescaling the weights after each unconstrained optimization step (so after every weight update loss.backward()?!)
Implications:
- I think they have found a very important insight of grokking and finding generalizing circuits more broadly.
- I'm still a bit skeptical of some of the claims and results. On some level "just fix your weight norm and the model generalizes" sounds too simple to be true for all tasks.
- I think this result could have big implications but I'm not yet sure whether they are positive or negative. On the one hand, finding generalizing circuits seems to solve some of the problems associated with bad out-of-distribution generalization. On the other hand, it likely speeds up capabilities.
I'm very unsure about this paper but intuitively it feels important. Thoughts?
Hmm, I haven't read the paper yet, but thinking about it, the easiest way to change the weight norm is just to multiply all weights by some factor α, but then in a network with ReLU activations and L layers, this would be completely equivalent to multiplying the output of the network by αL. In the overfitting regime where the network produces probability distributions where the mode is equal to the answer for all training tokens, the easiest way to decrease loss is just to multiply the output by a constant factor, essentially decreasing the entropy of the distribution forever, but this strategy fails at test-time because the mode is not equal to the answer there. So keeping the weight norm at some specified level might just be a way to prevent the network from taking the easy way towards decreasing training loss, and forcing it to find ways at constant-weight-norm to decrease loss, which would better generalize for the test-set.
I think this theory is probably part of the story, but it fails to explain Figure 2(b), where grokking happens in the presence of weight decay, even if you keep weight norm constant.