In section 3.7 of the paper, it seems like the descriptions ("6 in 5", etc) are inconsistent across the image, the caption, and the paragraph before them. What are the correct labels? (And maybe fix the paper if these are typos?)
This has been fixed now. Thanks for pointing it out! I'm sorry it took me so long to get to this.
I wonder if there is some way to alter the marginal return curves so that they are not diminishing, and see whether that removes polysemanticity from the trained network. This seems difficult to do at the outset, because a lot of features just are going to be of somewhat diminishing marginal utility for most real-world learning problems. But I wonder if there is some way to train a network, and then, based on the trained weights, do some fine-tuning using a loss that is set up so that the marginal returns to feature capacity are non-diminishing for the particular features learned so far.
Good question! As you suggest in your comment, increasing marginal returns to capacity induce monosemanticity, and decreasing marginal returns induce polysemanticity.
We observe this in our toy model. We didn't clearly spell this out in the post, but the marginal benefit curves labelled from A to F correspond to points in the phase diagram. At the top of the phase diagram where features are dense, there is no polysemanticity because the marginal benefit curves are increasing (see curves A and B). In the feature sparse region (points D, E, F), we see polysemanticity because the marginal benefit curves are decreasing.
The relationship between increasing/decreasing marginal returns and polysemanticity generalizes beyond our toy model. However, we don't have a generic technique to define capacity across different architectures and loss functions. Without a general definition, it's not immediately obvious how to regularize the loss for increasing returns to capacity.
You're getting at a key question the research brings up: can we modify the loss function to make models more monosemantic? Empirically, increasing sparsity increases polysemanticity across all models we looked at (figure 7 from the arXiv paper)*. According to the capacity story, we only see polysemanticity when there is decreasing marginal returns to capacity. Therefore, we hypothesize that there is likely a fundamental connection between feature sparsity and decreasing marginal returns. That is to say, we are suggesting that: if features are sparse and similar enough in importance, polysemanticity is optimal.
*Different models showed qualitatively different levels of polysemanticity as a function of sparsity. It seems possible that tweaking the architecture of a LLM could change the amount of polysemanticity, but we might take a performance hit for doing so.
Thanks for this.
we don't have a generic technique to define capacity across different architectures and loss functions
Got it. I imagine that for some particular architectures, and given some particular network weights, you can numerically compute the marginal returns to capacity curves, but that it's hard to express capacity analytically as a function of network weights since you really need to know what the particular features are in order to compute returns to capacity -- is that correct?
A few notes/questions about things that seem like errors in the paper (or maybe I'm confused — anyway, none of this invalidates any conclusions of the paper, but if I'm right or at least justifiably confused, then these do probably significantly hinder reading the paper; I'm partly posting this comment to possibly prevent some readers in the future from wasting a lot of time on the same issues):
1) The formula for here seems incorrect:
This is because W_i is a feature corresponding to the i'th coordinate of x (this is not evident from the screenshot, but it is evident from the rest of the paper), so surely what shows up in this formula should not be W_i, but instead the i'th row of the matrix which has columns W_i (this matrix is called W later). (If one believes that W_i is a feature, then one can see this is wrong already from the dimensions in the dot product not matching.)
2) Even though you say in the text at the beginning of Section 3 that the input features are independent, the first sentence below made me make a pragmatic inference that you are not assuming that the coordinates are independent for this particular claim about how the loss simplifies (in part because if you were assuming independence, you could replace the covariance claim with a weaker variance claim, since the 0 covariance part is implied by independence):
However, I think you do use the fact that the input features are independent in the proof of the claim (at least you say "because the x's are independent"):

Additionally, if you are in fact just using independence in the argument here and I'm not missing something, then I think that instead of saying you are using the moment-cumulants formula here, it would be much much better to say that independence implies that any term with an unmatched index is . If you mean the moment-cumulants formula here https://en.wikipedia.org/wiki/Cumulant#Joint_cumulants , then (while I understand how to derive every equation of your argument in case the inputs are independent), I'm currently confused about how that's helpful at all, because one then still needs to analyze which terms of each cumulant are 0 (and how the various terms cancel for various choices of the matching pattern of indices), and this seems strictly more complicated than problem before translating to cumulants, unless I'm missing something obvious.
3) I'm pretty sure this should say x_i^2 instead of x_i x_j, and as far as I can tell the LHS has nothing to do with the RHS:
(I think it should instead say sth like that the loss term is proportional to the squared difference between the true and predictor covariance.)
Thanks for this careful review! And sorry for wasting your time with these, assuming you're right. We'll hopefully look into this at some point soon.
I've uploaded a fixed version of this paper. Thanks so much for putting in the effort to point out these mistakes - I really appreciate that!
Thank you for this work. How feasible would it be to replicate these results using large neural networks (but still using synthetic training data where you can control feature sparsity directly)? What then would be the path to determining whether networks trained on real-world datasets behave according to this model?
We think this sort of approach can be applied layer-by-layer. As long as you know what the features are you can calculate dL/dC_i for each feature and figure out what's going on with that. The main challenge to this is feature identification: in a one layer model with synthetic data it's often easy to know what the features are. In more complicated settings it's much less clear what the "right" or "natural" features are...
Right! Two quick ideas:
-
Although it's not easy to determine the full set of "natural" features for arbitrary networks, still you might be able to solve an optimization problem that identifies the single feature with most negative marginal returns to capacity given the weights of some particular trained network. If you could do this then perhaps you could apply a regularization to the network that "flattens out" the marginal returns curve for just that one feature, then apply further training to the network and ask again which single feature has most negative marginal returns to capacity given the updated network weights, and again flatten out the marginal returns curve for that one feature, and repeat until there are no features with negative marginal returns to capacity. Doing this feature-by-feature would be too slow for anything but toy networks, I suppose, but if it worked for toy networks then perhaps it would point the way towards something more scalable.
-
Suppose instead you can find the least important (lowest absolute value of dL/dC_i) feature given some particular set of weights for a network and mask that feature out from all the inputs, and the iterate in the same way as above. In the third figure from the top in your post -- the one with the big vertical stack of marginal return curves -- you would be chopping off the features one-by-one from bottom to top, ideally until you have exactly as many features as you can "fit" monosemantically into a particular architecture. I suppose again that doing this feature-by-feature for anything but a toy model would be prohibitive, but perhaps there is a way to do it more efficiently. I wonder whether there is any way to "find the least important feature" and to "mask it out".
In both ideas I'm not sure how you're identifying features. Manual interpretability work on a (more complicated) toy model?
You write down an optimization problem over (say) linear combinations of image pixels, minimizing some measure of marginal returns to capacity given current network parameters (first idea) or overall importance as measured by absolute value of dL/dC_i, again given current network parameters (second idea). By looking just for the feature that is currently "most problematic" you may be able to sidestep the need to identify the full set of "features" (whatever that really means).
I don't know how exactly you would formulate these objective functions but it seems do-able no?
Oh I see! Sorry I didn't realize you were describing a process for picking features.
I think this is a good idea to try, though I do have a concern. My worry is that if you do this on a model where you know what the features actually are, what happens is that this procedure discovers some heavily polysemantic "feature" that makes better use of capacity than any of the actual features in the problem. Because dL/dC_i is not a linear function of the feature's embedding vector, there can exist superpositions of features which have greater dL/dC_i than any feature.
Anyway, I think this is a good thing to try and encourage someone to do so! I'm happy to offer guidance/feedback/chat with people interested in pursuing this, as automated feature identification seems like a really useful thing to have even if it turns out to be really expensive.

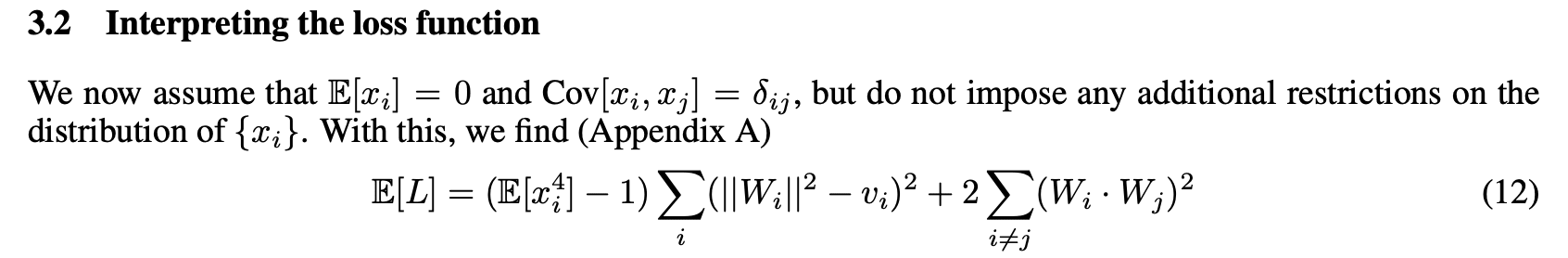

Elhage et al at Anthropic recently published a paper, Toy Models of Superposition (previous Alignment Forum discussion here) exploring the observation that in some cases, trained neural nets represent more features than they “have space for”--instead of choosing one feature per direction available in their embedding space, they choose more features than directions and then accept the cost of “interference”, where these features bleed over into each other. (See the SoLU paper for more on the Anthropic interpretability team’s take on this.)
We (Kshitij Sachan, Adam Scherlis, Adam Jermyn, Joe Benton, Jacob Steinhardt, and I) recently uploaded an Arxiv paper, Polysemanticity and Capacity in Neural Networks, building on that research. In this post, we’ll summarize the key idea of the paper.
We analyze this phenomenon by thinking about the model’s training as a constrained optimization process, where the model has a fixed total amount of capacity that can be allocated to different features, such that each feature can be ignored, purely represented (taking up one unit of capacity), or impurely represented (taking up some amount of capacity between zero and one units).
When the model purely represents a feature, that feature gets its own full dimension in embedding space, and so can be represented monosemantically; impurely represented features share space with other features, and so the dimensions they’re represented in are polysemantic.
For each feature, we can plot the marginal benefit of investing more capacity into representing that feature, as a function of how much it’s currently represented. Here we plot six cases, where one feature’s marginal benefit curve is represented in blue and the other in black.
These graphs show a variety of different possible marginal benefit curves. In A and B, the marginal returns are increasing–the more you allocate capacity to a feature, the more strongly you want to allocate more capacity to it. In C, the marginal returns are constant (and in this graph they happen to be equal for the two features, but there’s no reason why constant marginal returns imply equal returns in general). And then in D, E, and F, there are diminishing marginal returns.
Now, we can make the observation that, like in any budget allocation problem, if capacities are allocated optimally, the marginal returns for allocating capacity to any feature must be equal (if the feature isn’t already maximally or minimally represented). Otherwise, we’d want to take capacity away from features with lower dLi/dCi and give it to features with higher dLi/dCi .
In the case where we have many features with diminishing marginal returns, capacity will in general be allocated like this:
Here the circles represent the optimal capacity allocation for a particular total capacity.
This perspective suggests that polysemanticity will arise when there are diminishing marginal returns to capacity allocated to particular features (as well as in some other situations that we think are less representative of what goes on in networks).
In our paper, we do the following:
How important or useful is this? We’re not sure. For Redwood this feels like more of a side-project than a core research project. Some thoughts on the value of this work: