My actual claim is that learning becomes not just harder linearly, or quadratically (e.g. when you have to spend, say, an extra hour on learning the same amount of new material compared to what you used to need), but exponentially (e.g. when you have to spend, say, twice as much time/effort as before on learning the same amount of new material).
This is an interesting claim, but I'm not sure if it matches my own subjective experience. Though I also haven't dug deeply into math so maybe it's more true there - it seems to me like this could vary by field, where some fields are more "broad" while others are "deep".
And looking around, e.g. this page suggests that at least four different kinds of formulas are used for modeling learning speed, apparently depending on the domain. The first one is the "diminishing returns" curve, which sounds similar to your model:
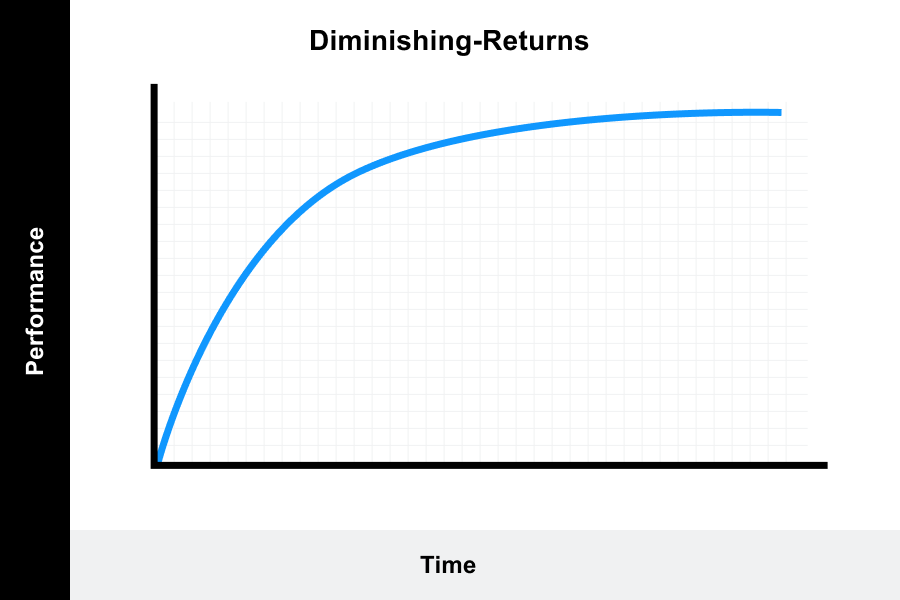
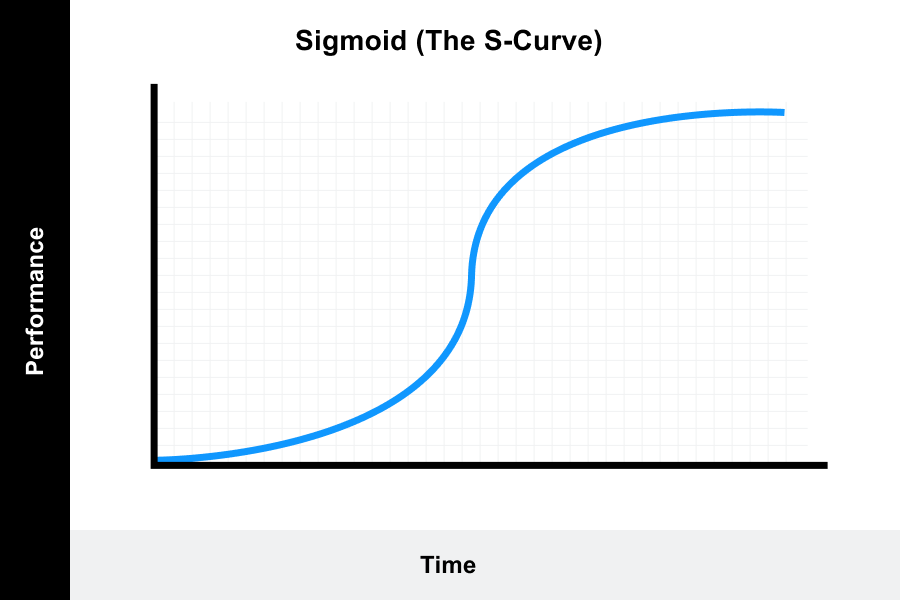
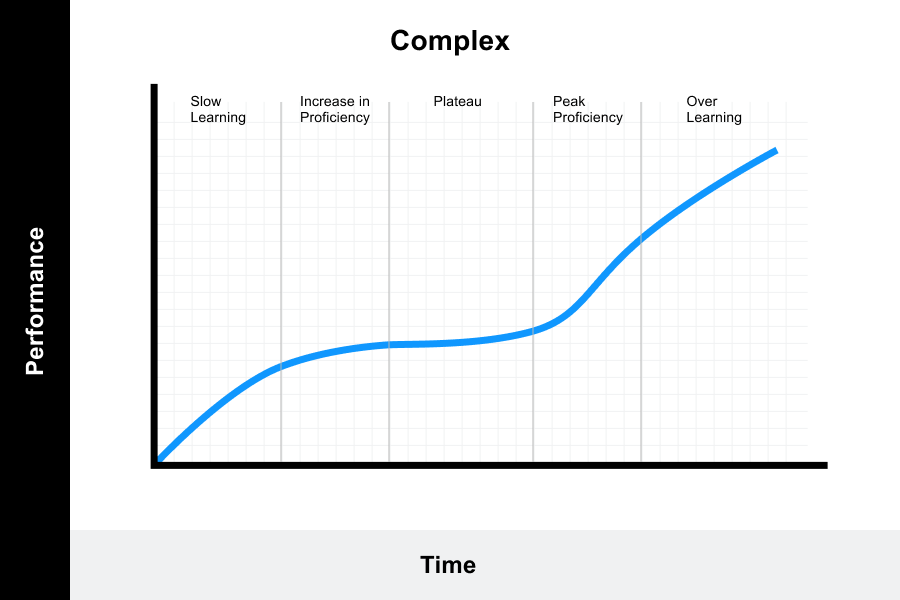
But it also includes graphs such as the s-curve (where initial progress is slow but then you have a breakthrough that lets you pick up more faster, until you reach a plateau) and the complex curve (with several plateaus and breakthroughs).
Why do I see this apparent phenomenon of inefficient learning important? One example I see somewhat often is someone saying "I believe in the AI alignment research and I want to contribute directly, and while I am not that great at math, I can put in the effort and get good." Sadly, that is not the case. Because learning is asymptotically inefficient, you will run out of time, money and patience long before you get to the level where you can understand, let alone do the relevant research: it's not the matter of learning 10 times harder, it's the matter of having to take longer than the age of the universe, because your personal exponent eventually gets that much steeper than that of someone with a natural aptitude to math.
This claim seems to run counter to the occasionally-encountered claim that people who are too talented at math may actually be outperformed by less talented students at one point, as the people who were too talented hit their wall later and haven't picked up the patience and skills for dealing with it, whereas the less talented ones will be used to slow but steady progress by then. E.g. Terry Tao mentions it:
Of course, even if one dismisses the notion of genius, it is still the case that at any given point in time, some mathematicians are faster, more experienced, more knowledgeable, more efficient, more careful, or more creative than others. This does not imply, though, that only the “best” mathematicians should do mathematics; this is the common error of mistaking absolute advantage for comparative advantage. The number of interesting mathematical research areas and problems to work on is vast – far more than can be covered in detail just by the “best” mathematicians, and sometimes the set of tools or ideas that you have will find something that other good mathematicians have overlooked, especially given that even the greatest mathematicians still have weaknesses in some aspects of mathematical research. As long as you have education, interest, and a reasonable amount of talent, there will be some part of mathematics where you can make a solid and useful contribution. It might not be the most glamorous part of mathematics, but actually this tends to be a healthy thing; in many cases the mundane nuts-and-bolts of a subject turn out to actually be more important than any fancy applications. Also, it is necessary to “cut one’s teeth” on the non-glamorous parts of a field before one really has any chance at all to tackle the famous problems in the area; take a look at the early publications of any of today’s great mathematicians to see what I mean by this.
In some cases, an abundance of raw talent may end up (somewhat perversely) to actually be harmful for one’s long-term mathematical development; if solutions to problems come too easily, for instance, one may not put as much energy into working hard, asking dumb questions, or increasing one’s range, and thus may eventually cause one’s skills to stagnate. Also, if one is accustomed to easy success, one may not develop the patience necessary to deal with truly difficult problems (see also this talk by Peter Norvig for an analogous phenomenon in software engineering). Talent is important, of course; but how one develops and nurtures it is even more so.
This is an interesting claim, but I'm not sure if it matches my own subjective experience. Though I also haven't dug deeply into math so maybe it's more true there - it seems to me like this could vary by field, where some fields are more "broad" while others are "deep".
My experience with math as an entire field is the opposite -- it gets easier to learn more to more I know. I think the big question is how you draw the box. If you draw it just around probability theory or something, the claim seems more plausible (though I still doubt it).
However, the efficiency in the world may be exponentially better for those who spend a lot of time getting marginally better. This is because they are better than others. For example, having ELO 2700 [not the exact number, just an illustration of the idea] in chess will put you near the top of all human players and allow earning money and ELO 2300 is useless.
Epistemic status: A speculation based on personal observations, but looks coherent to me. (Sorry, no links or literature search)
Summary: Studying a subject gets progressively harder as you learn more and more, and the effort required is conjectured to be exponential or worse, which means that sooner or later you hit the limit of what you can learn in a reasonable amount of time. If that limit is not where your skills/knowledge are yet useful, you have basically wasted your time compared to learning something else instead. Consider evaluating your aptitudes and the usability threshold before investing the proverbial 10,000 hours into something specific.
I have noticed this over and over, in my own life as well as watching and teaching others: It is usually not too hard to learn the very basics of something, be it math, music or basketball, and for awhile the effort you put in brings tangible rewards in terms of deeper understanding, better skills and more fluency. Different people, however, need a different amount of effort in different areas per amount of material learned (and retained), right off the bat. (This part seems pretty uncontroversial, unless one is ideologically against admitting that not all people are born all around equal, and that just because they aren't, it doesn't mean that it implies differences in moral weight or something.) This initial part of learning is basically linear: the gain is roughly proportional to the effort you put in. That initial "honeymoon" phase tends to peter out eventually.
Sooner or later, one notices that to make the same apparent amount of progress you have to put more effort than you used to. Maybe it's solving an equation that makes you sweat more, maybe you struggle to play a particularly challenging passage, maybe a certain dribbling drill leaves you frustrated. You can still get through it, but the process not nearly as much fun or easy as it used to feel. Maybe getting over the hump lets you make progress easier for awhile. Maybe drawing on your skills in other areas helps you get over the hump, if you are lucky. But still, the more you learn, the harder the learning process becomes, if not monotonically so, than on average.
My actual claim is that learning becomes not just harder linearly, or quadratically (e.g. when you have to spend, say, an extra hour on learning the same amount of new material compared to what you used to need), but exponentially (e.g. when you have to spend, say, twice as much time/effort as before on learning the same amount of new material). This is analogous to computational efficiency, and learning effort is at least O(exp(n)), asymptotically, where n is the amount of material learned. Which means that eventually it becomes too much. To prove one more theorem becomes an insurmountable effort, to code a somewhat more complicated algorithm takes more time than your company or your interviewer has. To learn to play the piano like a virtuoso would take you centuries. To reliably hit the hoop from half-court, or to get your golf score below X is forever out of reach, no matter how hard you try.
It doesn't mean, of course, that everyone hits the same wall: the effort required by two people with different aptitudes diverges exponentially. Say, your learning rate is X and someone else's is Y, the ratio of the amount of effort of the two of you is exp(Xn)/exp(Yn)=exp((X-Y)n), where n is the amount of material learned. So eventually one of you, given a comparable amount of effort, would be way ahead of the other.
Why do I see this apparent phenomenon of inefficient learning important? One example I see somewhat often is someone saying "I believe in the AI alignment research and I want to contribute directly, and while I am not that great at math, I can put in the effort and get good." Sadly, that is not the case. Because learning is asymptotically inefficient, you will run out of time, money and patience long before you get to the level where you can understand, let alone do the relevant research: it's not the matter of learning 10 times harder, it's the matter of having to take longer than the age of the universe, because your personal exponent eventually gets that much steeper than that of someone with a natural aptitude to math. Another example is the sports scouts: the good ones intuitively see the limits of someone's athletic skills very early on, and can confidently say "This one will never play in the NBA" long before it becomes apparent to the aspiring player themselves.
One objection to this conclusion is that we see people of comparable skills all the time, much more often than those who are way ahead of the rest. Sure, some seem smarter and more capable than others, but not incredibly so. My take on it is two-fold: one is that a specific niche tends to include people of roughly similar skills, so the difference in the learning abilities ((X-Y) above) is not very large, and two is that very few people actually push to the point where the exponent becomes too steep to handle and instead stop learning new things much earlier that that. Sure, if you are a programmer you may still learn Rust or some new Framework.js, but that is not really the kind of learning that requires you to climb the the exponent, it's more like going sideways.
It is also worth noting the synergies: the aptitudes are not all orthogonal to each other, so ascending a different, easier path can get you closer to the same exponentially tall summit, if not quite on top of it. You can learn (almost) the same math in different ways. Even apparently independent skills can come together in unexpected ways to make the climb easier.
Eventually, however, if you keep working in earnest, no matter what you try and how hard you apply yourself, that exponential limit will get you. So, what to do to minimize frustration? One common intuitive approach is to... stop learning early. That's what most people do, unless forced to, they learn just enough to get by on what they know. Really, it works. Even if you want to advance. To quote HPMoR "for although you are ambitious, you have no ambition." There is usually some room in the middle.
Assuming you do have ambition, you probably ought to plan way ahead. How do you achieve something extraordinary, or at least above ordinary, given what you know about yourself? Presumably, you want to be able to perform at the top level in the field of your choosing, and that means a couple of things: you are somewhere around, say, top 0.1% in your area, including potential synergies, and the field itself has not yet attracted a lot of those at the 0.01% level, so some low hanging (for you) fruit is still left. Otherwise you will max out long before you cross the threshold of where the skills you have learned become useful, and that's a shame. Now, if only it was so easy to evaluate all these unknowns before embarking on that learning journey...