1 Answers sorted by
90
This incentivises some weird stuff.
In this setup, individuals are represented by vectors of length in dimensional space. (where is the number of issues voted on) The combined vote is just the sum of all the vectors. Collusion just means adding the vectors, and then pointing both vectors in that direction.
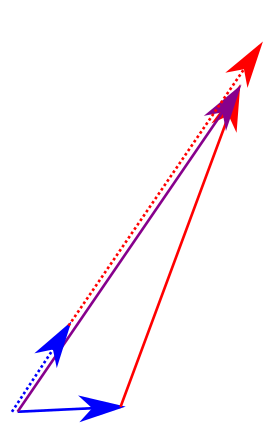
Red and blue are the 2 voters (red is richer). Purple is the combined consequence of the votes. Dotted red and blue are what happens when they collude.
Lets suppose its a token based vote, and everyone has 1 token.
Everyone else is a naive pro puppy (up) voter. You are a strategic pro frog voter.
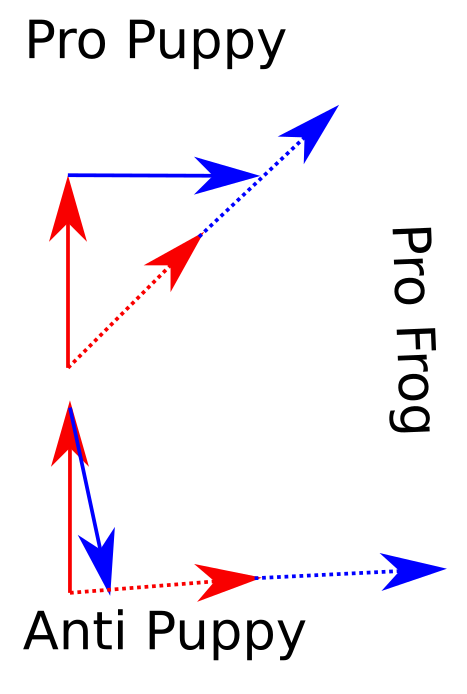
If you vote your actual preferences, the result is as shown above. Your preferences to pro frog get combined with the puppy lovers. However, you could vote almost entirely anti puppy, with only a trace of pro frog. The pro and anti puppy sections almost cancel out, meaning that when your vote is colluded with that of a puppy lover, you get 2 (almost) entirely pro frog votes.
(There is another sensible means of colluding, that's having the same results on the election, but spending less money to do it. So this would give people partial refunds, and not change the result. This kind of encourages voting for really unpopular positions, but doesn't directly change the election result. Its basically the top diagram, except the dotted arrows are scaled down so that they add to the purple arrow.)
I've been noodling on an example, and did notice this kind of problem. Currently working on what would happen if collusion was limited to vote trades between pairs of issues you directionally agree on. So only "I vote +1 puppy, +2 frog; you vote +2 puppy, +1 frog; we transform into +1.58 puppy, +1.58 frog apiece".
If everyone ends up with the same vote distribution, I think it removes the incentive for colluding beforehand, but it also means the vote is no longer meaningfully quadratic. The rank ordering of the candidates will be in order of how many total points were spent on them, and you basically end up with score voting.
edit: I assume that the automatic collusion mechanism is something like averaging the two ballots' allocations for each candidate, which does not change the number of points spent on each candidate. If instead some ballots end up causing more points to be spent on their preferred candidates than they initially had to work with, there are almost definitely opportunities for strategic voting and beforehand collusion.
I'm not sure I follow. what is the mechanics that "collude" implies in this proposal? Just a reduction in cost for the stronger preferences (if I spend 16 for 4 votes, and you spend 4 for 2 votes, I get a discount to 14, which is 9 for 3 votes and a gift to you of 5 so you can also spend 9 for 3 votes)?
Or perhaps some form of enforced trade? If I spend 16 on issue A and 4 on issue B, and you're doing the reverse, it gets automatically recalculated as if we both spent 9 on A and B - same votes, but we each spend 2 units less (or more votes for same price, if fractional votes are allowed).
A specific worked example with just a few participants would help a lot. And might even answer your question directly as to "what would happen". My suspicion is it would move the equilibrium closer to fixed-cost cumulative voting.
a specific worked example
Yep that's my next step if no one "just knows" or links to a paper. :D
I was thinking about enforced trades, more votes for the same price (fractional is allowed).
Wondering what happens if you have https://en.wikipedia.org/wiki/Quadratic_voting but with automated collusion - after all votes are in, pair two people and have them collude automatically, splitting implied utility equally, repeat over and over until everyone has the same distribution, do this whole process a million times, take the majority winners as winners.
Does that incentivize you to actually vote your real preferences rather than trying to collude beforehand?
Okay you won't actually end up with everyone having the same distribution. But still, do it until "convergence", then take majority winners, and see who wins most under a million random paths to convergent collusions, and take those as winners.