Epistemic Status
This started out as a shortform and is held to the same epistemic standards that I do for my Twitter account. It however became too long for that medium, so I felt the need to post it elsewhere.
I feel it's better to post my rough and unpolished thoughts than to not post them at all, so hence.
Introduction
One significant way I've changed my views related to risks from strongly superhuman intelligence (compared to 2017 bingeing LW DG) is that I no longer believe intelligence to be "magical".
During my 2017 binge of LW, I recall Yudkowsky suggesting that a superintelligence could infer the laws of physics from a single frame of video showing a falling apple (Newton apparently came up with his idea of gravity from observing a falling apple).
I now think that's somewhere between deeply magical and utter nonsense. It hasn't been shown that a perfect Bayesian engine (with [a] suitable [hyper]prior[s]) could locate general relativity or (even just Newtonian mechanics) in hypothesis space from a single frame of video.
I'm not even sure a single frame of video of a falling apple has enough bits to allow one to make that distinction in theory.
Edit
The above is based on a false recollection of what Yudkowsky said (I leave it anyway because the comments have engaged with it). Here's the relevant excerpt from "That Alien Message":
A Bayesian superintelligence, hooked up to a webcam, would invent General Relativity as a hypothesis—perhaps not the dominant hypothesis, compared to Newtonian mechanics, but still a hypothesis under direct consideration—by the time it had seen the third frame of a falling apple. It might guess it from the first frame, if it saw the statics of a bent blade of grass.
I still disagree somewhat with the above, but it's a weaker disagreement — this is a weaker claim than I misrecalled Yudkowsky as making — I apologise for any harm/misunderstanding my carelessness (I should have just tracked down the original post) caused.
I think that I need to investigate at depth what intelligence (even strongly superhuman intelligence) is actually capable of, and not just assume that intelligence can do anything not explicitly forbidden by the fundamental laws. The relevant fundamental laws with a bearing on cognitive and real-world capabilities seem to be:
- Physics
- Computer Science
- Information Theory
- Mathematical Optimisation
- Decision & Game Theory
The Relevant Question: Marginal Returns to Real World Capability of Cognitive Capabilities
I've done some armchair style thinking on "returns to real-world capability" of increasing intelligence, and I think the Yudkowsky style arguments around superintelligence are quite magical.
It seems doubtful that higher intelligence would enable that. E.g. marginal returns to real-world capability from increased predictive power diminish at an exponential rate. Better predictive power buys less capability at each step, and it buys a lot less. I would say that the marginal returns are "sharply diminishing".
An explanation of "significantly/sharply diminishing":

Sharply Diminishing Marginal Returns to Real World Capabilities From Increased Predictive Accuracy
A sensible way of measuring predictive accuracy is something analogous to . The following transitions:
All make the same incremental jump in predictive accuracy.
We would like to measure the marginal return to real-world capability of increased predictive accuracy. The most compelling way I found to operationalise "returns to real-world capability" was monetary returns.
I think that's a sensible operationalization:
- Money is the basic economic unit of account
- Money is preeminently fungible
- Money can be efficiently levered into other forms of capability via the economy.
- I see no obviously better proxy.
(I will however be interested in other operationalisations of "returns to real-world capability" that show different results).
The obvious way to make money from beliefs in propositions is by bets of some form. One way to place a bet and reliably profit is insurance. (Insurance is particularly attractive because in practice, it scales to arbitrary confidence and arbitrary returns/capital).
Suppose that you sell an insurance policy for event , and for each prospective client , you have a credence that would not occur to them . Suppose also that you sell your policy at .
At a credence of , you cannot sell your policy for . At a price of and given the credence of , your expected returns will be for that customer. Assume the given customer is willing to pay at most for the policy.
If your credence in not happening increased, how would your expected returns change? This is the question we are trying to investigate to estimate real-world capability gains from increased predictive accuracy.
The results are below:
As you can see, the marginal returns from linear increases in predictive accuracy are give by the below sequence:
(This construction could be extended to other kinds of bets, and I would expect the result to generalise [modulo some minor adjustments] to cross-domain predictive ability.
Alas, a shortform [this started as a shortform but ended up crossing the 1,000 words barrier, so I moved it] is not the place for such elaboration).
Thus returns to real-world capability of increased predictive accuracy are sharply diminishing.
One prominent class of scenario in which the above statement is false is when competing against other agents. In competitions with "winner take all" dynamics, better predictive accuracy has more graceful returns. I'll need to think further about various multi agent scenarios and model them better/in more detail.
Marginal Returns to Real World Capabilities From Other Cognitive Capabilities
Of course, predictive accuracy is just one aspect of intelligence, there are many others:
- Planning
- Compression
- Deduction
- Induction
- Other symbolic reasoning
- Concept synthesis
- Concept generation
- Broad pattern matching
- Etc.
And we'd want to investigate the relationship for aggregate cognitive capabilities/"general intelligence". The example I illustrated earlier merely sought to demonstrate how returns to real-world capability could be "sharply diminishing".
Marginal Returns to Cognitive Capabilities
Another inquiry that's important to determining what intelligence is actually capable of is the marginal returns to investment of cognitive capabilities towards raising cognitive capabilities.
That is if an agent was improving its own cognitive architecture (recursive self improvement) or designing successor agents, how would the marginal increase in cognitive capabilities across each generation behave? What function characterises it?
Marginal Returns of Computational Resources
This isn't even talking about the nature of marginal returns to predictive accuracy from the addition of extra computational resources.
By "computational resources" I mean the following:
- Training compute
- Inference compute
- Training data
- Inference data
- Accessible memory
- Bandwidth
- Energy/power
- Etc.
- An aggregation of all of them
That could further bound how much capability you can purchase with the investment of additional economic resources. If those also diminish "significantly" or "sharply", the situation becomes that much bleaker.
Marginal Returns to Cognitive Reinvestment
The other avenue to raising cognitive capabilities is the investment of cognitive capabilities themselves. As seen when designing successor agents or via recursive self-improvement.
We'd also want to investigate the marginal returns to cognitive reinvestment.
My Current Thoughts
Currently, I think strongly superhuman intelligence would require herculean effort. I am much less confident that bootstrapping to ASI would necessarily be as easy as recursive self-improvement or "scaling" up the expenditure of computational resources. I'm unconvinced that a hardware overhang would be sufficient (marginal returns may diminish too fast for it to be sufficient).
I currently expect marginal returns to real-world capability will diminish significantly or sharply for many cognitive capabilities (and the aggregate of them) across some "relevant cognitive intervals".
I suspect that the same will prove to be true for marginal returns to cognitive capabilities of investing computational resources or other cognitive capabilities.
I don't plan to rely on my suspicions and would want to investigate these issues at extensive depth (I'm currently planning to pursue a Masters and afterwards PhD, and these are the kinds of questions I'd like to research when I do so).
By "relevant cognitive intervals", I am gesturing at the range of general cognitive capabilities an agent might belong in.
Humans being the only examples of general intelligence we are aware of, I'll use them as a yardstick.
Some "relevant cognitive intervals" that seem particularly pertinent:
- Subhuman to near-human
- Near-human to beginner human
- Beginner human to median human professional
- Median human professional to expert human
- Expert human to superhuman
- Superhuman to strongly superhuman
Conclusions and Next Steps
The following questions:
- Marginal returns to cognitive capabilities from the investment of computational resources
- Marginal returns to cognitive capabilities from:
- Larger cognitive engines
- E.g. a brain with more synapses
- E.g. a LLM with more parameters
- Faster cognitive engines
- Better architectures/algorithms
- E.g. Transformers vs LSTM
- Coordination with other cognitive engines
- A "hive mind"
- Swarm intelligence
- Committees
- Corporations
- Larger cognitive engines
- Marginal returns to computational resources from economic investment
- How much more computational resources can you buy by throwing more money directly at computational resources?
- What’s the behaviour of the cost curves of computational resources?
- Economies of scale
- Production efficiencies
- What’s the behaviour of the cost curves of computational resources?
- How much more computational resources can you buy by throwing more money at cognitive labour to acquire computational resources?
- How does investment of cognitive labour affect the cost curves of computational resources?
- How much more computational resources can you buy by throwing more money directly at computational resources?
- Marginal returns to real world capabilities from the investment of cognitive capabilities
- Marginal returns to real world capabilities from investment of economic resources
(Across the cogntive intervals of interest).
Are questions I plan to investigate in depth in the future.
The core problem remains computational complexity.
Statements like "does this image look reasonable" or saying "you pay attention to regularities in the data", or "find the resolution by searching all possible resolutions" are all hiding high computational costs behind short English descriptions.
Let's consider the case of a 1280x720 pixel image.
That's the same as 921600 pixels.
How many bytes is that?
It depends. How many bytes per pixel?[1] In my post, I explained there could be 1-byte-per-pixel grayscale, or perhaps 3-bytes-per-pixel RGB using [0, 255] values for each color channel, or maybe 6-bytes-per-pixel with [0, 65535] values for each color channel, or maybe something like 4-bytes-per-pixel because we have 1-byte RGB channels and a 1-byte alpha channel.
Let's assume that a reasonable cutoff for how many bytes per pixel an encoding could be using is say 8 bytes per pixel, or a hypothetical 64-bit color depth.
How many ways can we divide this between channels?
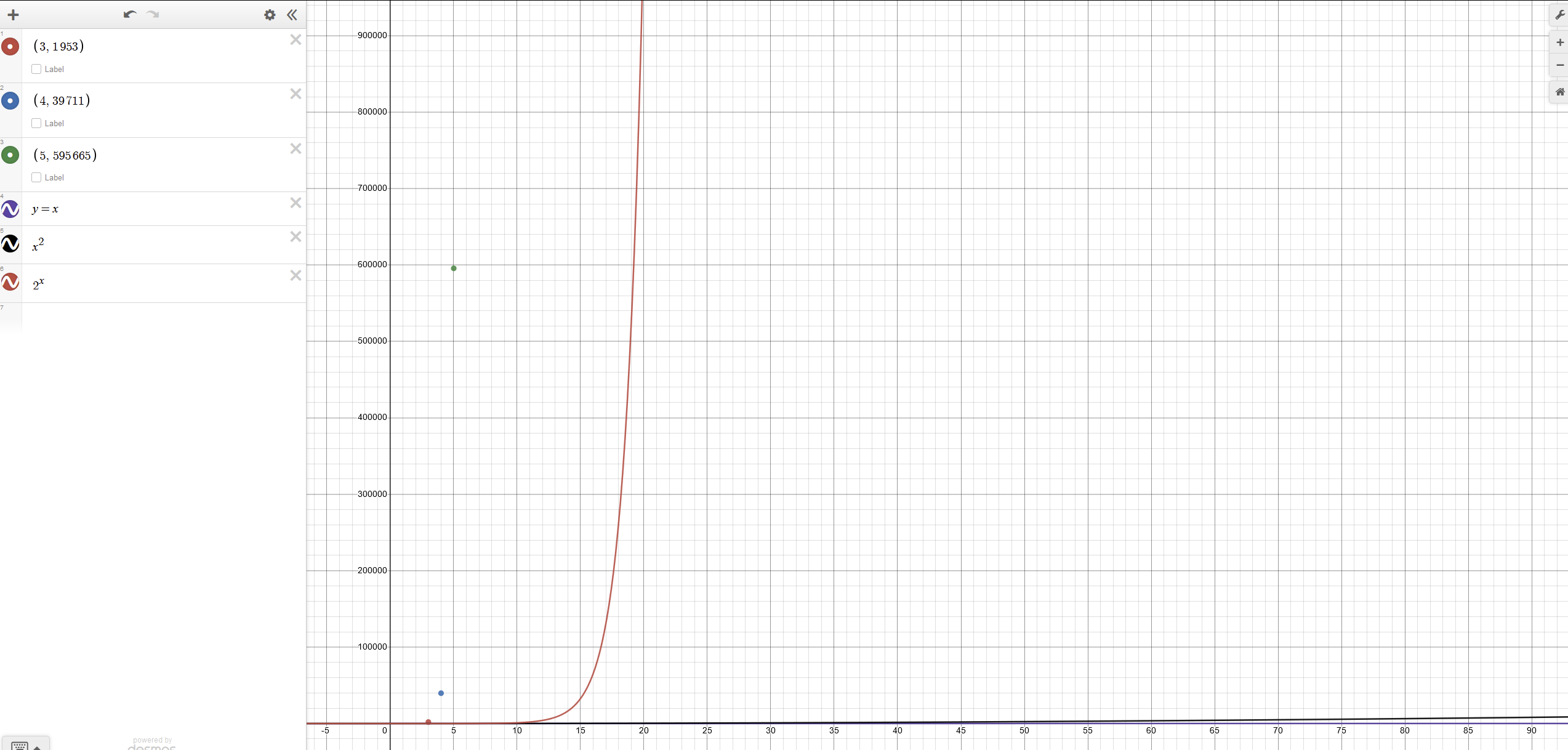
If we assume 3 channels, it's 1953.
If we assume 4 channels, it's 39711.
Also if it turns out to be 5 channels, it's 595665.
This is a pretty fast growing function. The following is a plot.
Note that the red line is
O(2^N)and the black line barely visible at the bottom isO(N^2).N^2is a notorious runtime complexity because it's right on the threshold of what is generally unacceptable performance.[2]Let's hope that this file isn't actually a frame buffer from a graphics card with 32 bits per channel or a 128 bit per pixel / 16 byte per pixel.
Unfortunately, we still need to repeat this calculation for all of the possibilities for how many bits per pixel this image could be. We need to add in the possibility that it is 63 bits per pixel, or 62 bits per pixel, or 61 bits per pixel.
In case anyone wants to claim this is unreasonable, it's not impossible to have image formats that have RGBA data, but only 1 bit associated with the alpha data for each pixel. [3]
And for each of these scenarios, we need to question how many channels of color data there are.
You actually ran into this problem yourself.
Summing up all of the possibilities above is left as an exercise for the reader, and we'll call that sum
K.Without loss of generality, let's say our image was encoded as 3 bytes per pixel divided between 3 RGB color channels of 1 byte each.
Our 1280x720 image is actually 2764800 bytes as a binary file.
But since we're decoding it from the other side, and we don't know it's 1280x720, when we're staring at this pile of 2764800 bytes, we need to first assume how many bytes per pixel it is, so that we can divide the total bytes by the bytes per pixel to calculate the number of pixels.
Then, we need to test each possible resolutions as you've suggested.
The number of possible resolutions is the same as the number of divisors of the number of pixels. The equation for providing an upper bound is
exp(log(N)/log(log(N)))[4], but the average number of divisors is approximatelylog(N).Oops, no it isn't!
Files have headers! How large is the header? For a bitmap, it's anywhere between 26 and 138 bytes. The JPEG header is at least 2 bytes. PNG uses 8 bytes. GIF uses at least 14 bytes.
Now we need to make the following choices:
Once we've made our choices above, then we multiply that by
log(N)for the number of resolutions to test, and then we'll apply the suggested metric. Remember that when considering the different pixel formats and ways the color channel data could be represented, the number wasK, and that's what we're multiplying bylog(N).What you're describing here is actually similar to a common metric used in algorithms for automatically focusing cameras by calculating the contrast of an image, except for focusing you want to maximize contrast instead of minimize it.
The interesting problem with this metric is that it's basically a one-way function. For a given image, you can compute this metric. However, minimizing this metric is not the same as knowing that you've decoded the image correctly. It says you've found a decoding, which did minimize the metric. It does not mean that is the correct decoding.
A trivial proof:
A slightly less trivial proof:
Nbytes of image data, there are2^(N*8)possible bit patterns.2^(8*8)possible bit patterns.N > 8, there are more bit patterns than values allowed in a double, so multiple images need to map to the same metric.The difference between our
2^(2764800*8)image space and the2^64metric is, uhhh,10^(10^6.8). Imagine10^(10^6.8)pigeons. What a mess.[5]The metric cannot work as described. There will be various arbitrary interpretations of the data possible to minimize this metric, and almost all of those will result in images that are definitely not the image that was actually encoded, but did minimize the metric. There is no reliable way to do this because it isn't possible. When you have a pile of data, and you want to reverse meaning from it, there is not one "correct" message that you can divine from it.[6] See also: numerology, for an example that doesn't involve binary file encodings.
Even pretending that this metric did work, what's the time complexity of it? We have to check each pixel, so it's
O(N). There's a constant factor for each pixel computation. How large is that constant? Let's pretend it's small and ignore it.So now we've got
K*O(N*log(N))which is the time complexity of lots of useful algorithms, but we've got that awkward constantKin the front. Remember that the constantKreflects the number of choices for different bits per pixel, bits per channel, and the number of channels of data per pixel. Unfortunately, that constant is the one that was growing a rate best described as "absurd". That constant is the actual definition of what it means to have no priors. When I said "you can generate arbitrarily many hypotheses, but if you don't control what data you receive, and there's no interaction possible, then you can't rule out hypotheses", what I'm describing is this constant.What I care about is the difference between:
1. Things that are computable.
2. Things that are computable efficiently.
These sets are not the same.
Capabilities of a superintelligent AGI lie only in the second set, not the first.
It is important to understand that a superintelligent AGI is not brute forcing this in the way that has been repeatedly described in this thread. Instead the superintelligent AGI is going to use a bunch of heuristics or knowledge about the provenance of the binary file, combined with access to the internet so that it can just lookup the various headers and features of common image formats, and it'll go through and check all of those, and then if it isn't any of the usual suspects, it'll throw up metaphorical hands, and concede defeat. Or, to quote the title of this thread, intelligence isn't magic.
This is often phrased as bits per pixel, because a variety of color depth formats use less than 8 bits per channel, or other non-byte divisions.
Refer to https://accidentallyquadratic.tumblr.com/ for examples.
A fun question to consider here becomes: where are the alpha bits stored? E.g. if we assume 3 bytes for RGB data, and then we have the 1 alpha bit, is each pixel taking up 9 bits, or are the pixels stored in runs of 8 pixels followed by a single "alpha" pixel with 8 bits describing the alpha channels of the previous 8 pixels?
https://terrytao.wordpress.com/2008/09/23/the-divisor-bound/
https://en.wikipedia.org/wiki/Pigeonhole_principle
The way this works for real reverse engineering is that we already have expectations of what the data should look like, and we are tweaking inputs and outputs until we get the data we expected. An example would be figuring out a camera's RAW format by taking pictures of carefully chosen targets like an all white wall, or a checkerboard wall, or an all red wall, and using the knowledge of those targets to find patterns in the data that we can decode.