Summary
- I sandwich the sparse layer in a sparse autoencoder (SAE) between non-sparse lower-dimensional layers and refer to this as a deep SAE.
- I find that features from deep SAEs are at least as interpretable as features from standard shallow SAEs.
- I claim that this is not a tremendously likely result if you assume that the success of SAEs is entirely explained by the accuracy of the superposition hypothesis.
- I speculate that perhaps by relaxing our adherence to the concrete principles laid out by the superposition hypothesis, we could improve SAEs in new ways.
Introduction
Context
Instead of rehashing the superposition hypothesis and SAEs, I will just link these wonderful resources: Toy Models of Superposition and Towards Monosemanticity.
Motivations
My sense is that the standard justification for the success of SAEs is that the superposition hypothesis is just an accurate model of neural network function, which directly translates to SAE effectiveness. While many of the arguments for the superposition hypothesis are compelling, I had a growing sense that the superposition hypothesis was at least not a sufficient explanation for the success of SAEs.
This sense came from, for example, inconsistencies between empirical findings in the posts linked above, for example that features will take similar directions in activation space if they don’t co-occur often, but also if they have similar effects on downstream model outputs, which seems contradictory in many cases. I won't elaborate too much on this intuition because (1) I don’t think understanding this intuition is actually that necessary to appreciate these results even if it served to initiate the project, (2) in hindsight, I don’t even think that these results strongly confirm my original intuition (but they also don’t oppose it).
Ultimately, I posited that, if there is some unidentified reason for the success of SAEs, it might be that sparsity is just a property of representations that us humans prefer, in some more abstract sense. If this were true, we should directly aim our SAEs to produce the most faithful and sparse representations of neural network function as possible, possibly abandoning some of the concrete principles laid out by the superposition hypothesis. And it seems that the obvious way to do this is to add more layers.
I'm posting my work so far because:
- I want to see if I'm missing something obvious, and to get feedback more generally.
- If the results are valid, then I think they may be interesting for people in mechanistic interpretability.
- I am hoping to connect with people who are interested in this area.
Results
What do I mean by deep SAE?
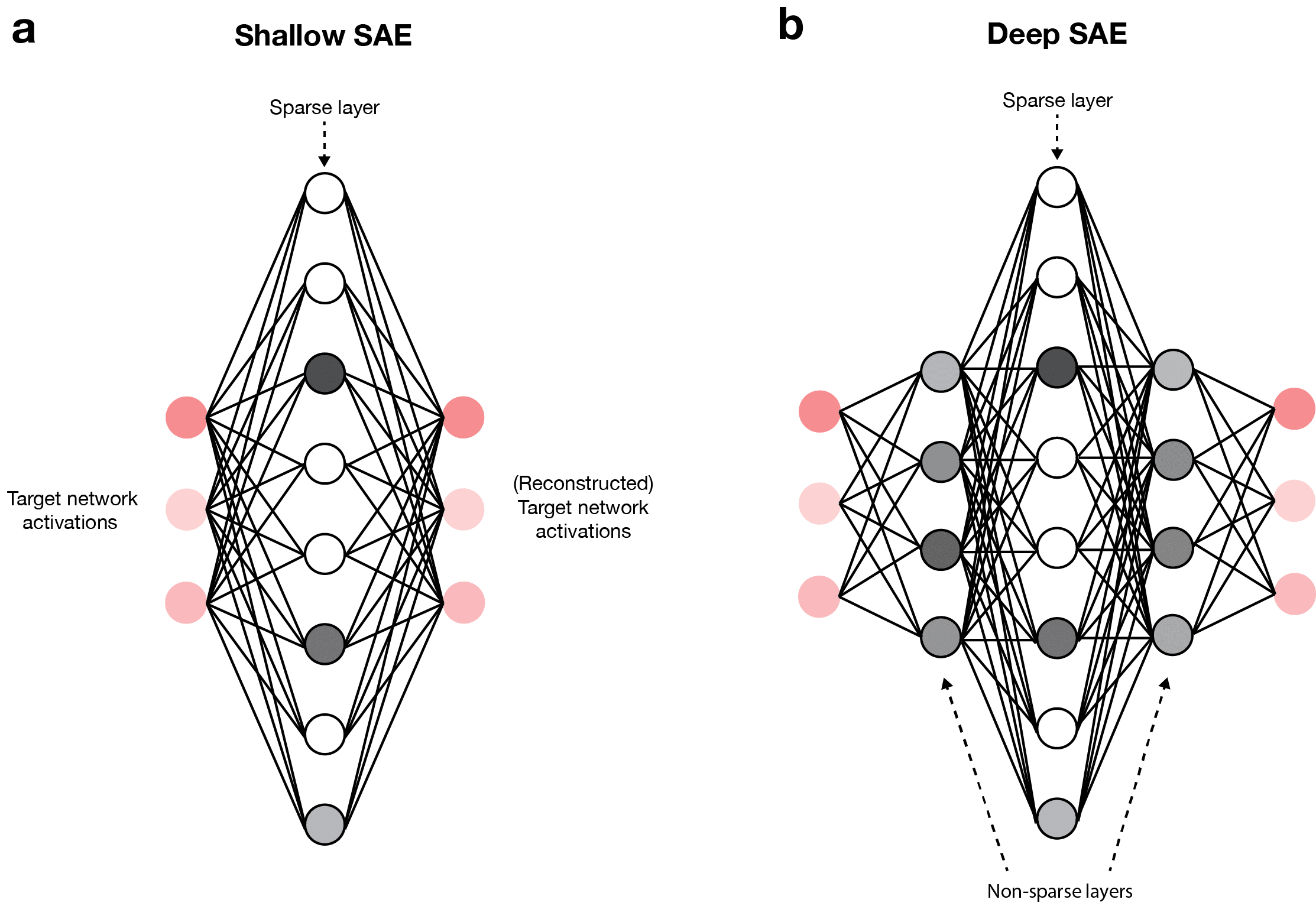
Standard applications of sparse autoencoders to the interpretation of neural networks use a single sparsely activating layer to reconstruct the activations of the network being interpreted (i.e., the target network) (Fig. 1a). This architecture will be referred to as a shallow SAE.
Here, I propose using deep SAEs for interpreting neural networks. Abstractly, this includes the addition of more layers (either non-sparse or sparse) to a shallow SAE. Concretely, the implementation I use here involves sandwiching a single sparse layer between one or more non-sparse layers (Fig. 1b). Throughout this work, all of the deep SAEs I present will take this structure and, moreover, the dimensions of the non-sparse layers will have reflection symmetry across the sparse layer (i.e., if there are non-sparse layers with dimensions 256 and 512 before the sparse layer, then there will be non-sparse layers with dimensions 512 and 256 after the sparse layer). In describing deep SAE architectures, I will sometimes use shorthand like “1 non-sparse” which, in this case, would just mean that there is one non-sparse layer before the sparse layer and one non-sparse layer after it.
In the experiments below, I use tied initialization for the encoder and decoder matrices, as previously described, which is only possible because of the symmetry of the encoder and decoder layers as described above. I also constrained the columns for all decoder matrices to unit norm, including those producing hidden layer activations (i.e., not just the final decoder matrix), as previously described. This unit norm constraint empirically showed to reduce dead features and stabilize training, particularly for deeper SAEs. I subtract the mean and divide by the norm across the dimension before using LLM activations for SAE input and analysis. I use ReLU activation functions for all SAE layers, and I use a top-k activation function for the sparse layer. I used two different strategies to reduce dead neurons: dead neuron resampling, and a new approach, where I penalize the mean of the square of the sparse feature activations, which I will refer to as activation decay.
SAE depth improves the reconstruction sparsity frontier
A common measure of SAE performance is how well it can reconstruct the activations (as measured by the MSE) at a given level of sparsity. Deep SAEs perform better than shallow SAEs on this metric (Fig. 2), which is unsurprising given that they are strictly more expressive. Here, I show the normalized MSE (i.e., the variance explained), which is the MSE of the SAE reconstructions divided by the MSE from predicting the mean activation vector. All of these SAEs were trained to reconstruct the activations of the residual stream after layer 8 of GPT2-small, where activations were collected on the common crawl dataset. I applied activation decay (with a coefficient of 1e-3) to both the deep and narrow SAE and neuron resampling to only the shallow SAE. This experiment uses a smaller number of sparse features for its SAEs than the next experiment and excludes deep SAEs beyond 1 non-sparse layer due to time and compute budget constraints.
It should be noted that this really says nothing about the interpretability of deep SAEs. A lower MSE does imply a more faithful representation of the true underlying network dynamics, but a low MSE may coexist with uninterpretable and/or polysemantic features.

Deep SAE features match or exceed shallow SAE features in automated interpretability scores
The real test for deep SAEs is not the faithfulness of their reconstructions (as we would expect them to perform well on this), but how interpretable their features are. To test this, I trained SAEs of various depths and passed their sparse features through an automated interpretability pipeline developed by EleutherAI to attain average interpretability scores. This automated interpretability pipeline involves choosing a particular feature, showing examples of text on which that feature activates to an LLM, like Claude, and asking it to generate an explanation of that feature, and finally, showing that explanation to another LLM and measuring the accuracy to which it’s able to predict whether that feature activates for unlabeled snippets of text. I conducted two variants of this test: detection and fuzzing. Detection involves measuring the accuracy of predictions of whether the feature activated at all in a snippet, and fuzzing involves measuring the accuracy of predictions of which words that feature activated on in the snippet.
Three SAEs were trained, each with 24576 sparse features and k=128, on the residual stream after layer 8 of GPT2-small. The first was a shallow SAE; the second was a deep SAE with one non-sparse layer of dimension 1536 (2x the dimension of GPT2-small) added to each side of the sparse layer, so, the dimensions of each layer, in order, are 1536, 24576, 1536; and the third SAE was also deep, with 2 non-sparse layers added to each side of the sparse layer, with dimensions 1536 (2x GPT2 dimension) and 3072 (4x GPT2 dimension), so the layer dimensions are 1536, 3072, 24576, 3072, 1536. I trained all SAEs with activation decay with a coefficient of 1e-3 (dead neuron resampling was not used for the shallow SAE in contrast to the previous experiment, in an attempt to reduce confounders).
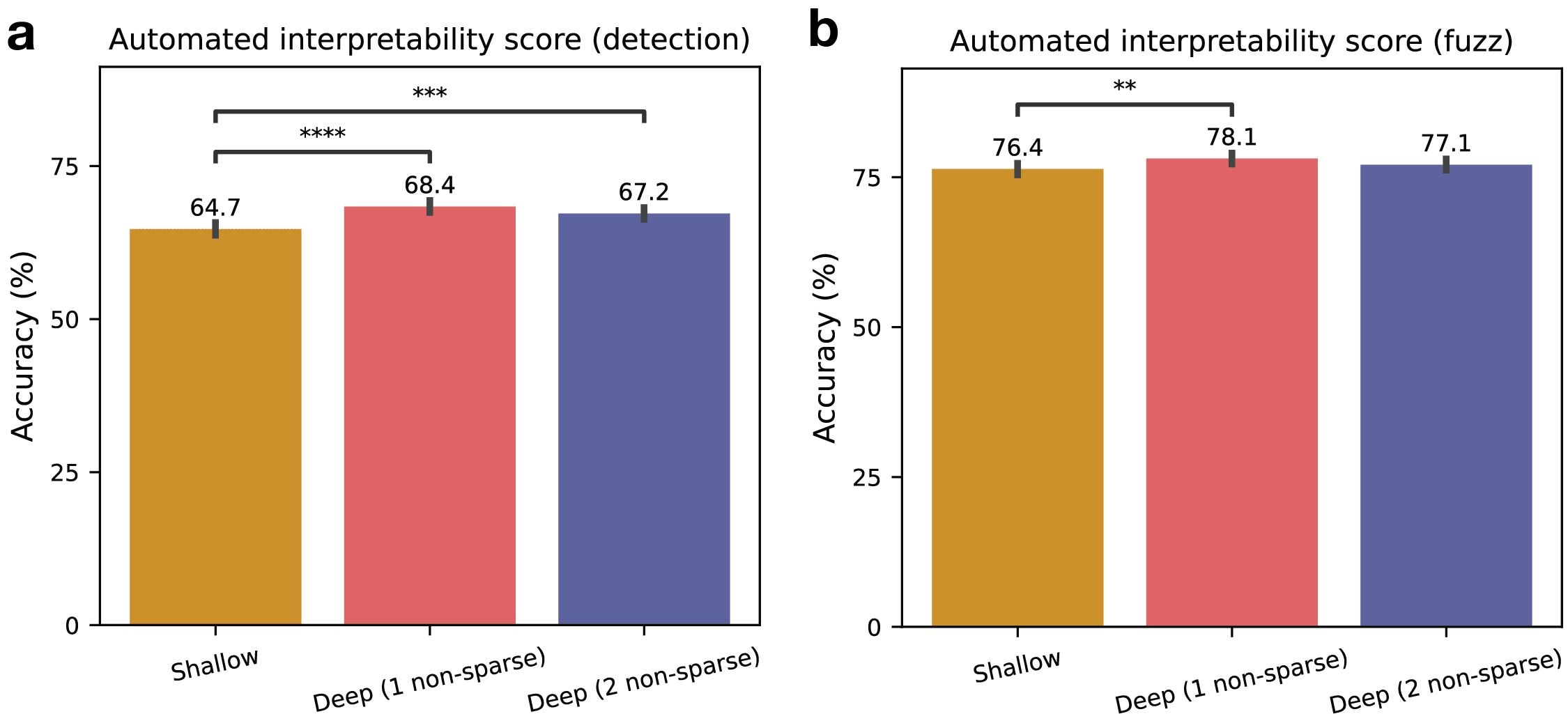
Overall, we see that deep SAE features are just as interpretable as shallow SAE features by both of these automated interpretability measures (Fig. 3). Neither the 1 non-sparse layer nor the 2 non-sparse layer SAE show interpretability scores lower than the shallow SAE, and both the 1 non-sparse layer and 2 non-sparse layer SAEs actually score slightly higher than the shallow SAE on the detection task. It would also be useful to run this experiment while controlling for the total parameter count, by decreasing the dimension of the sparse layer for deeper SAEs.
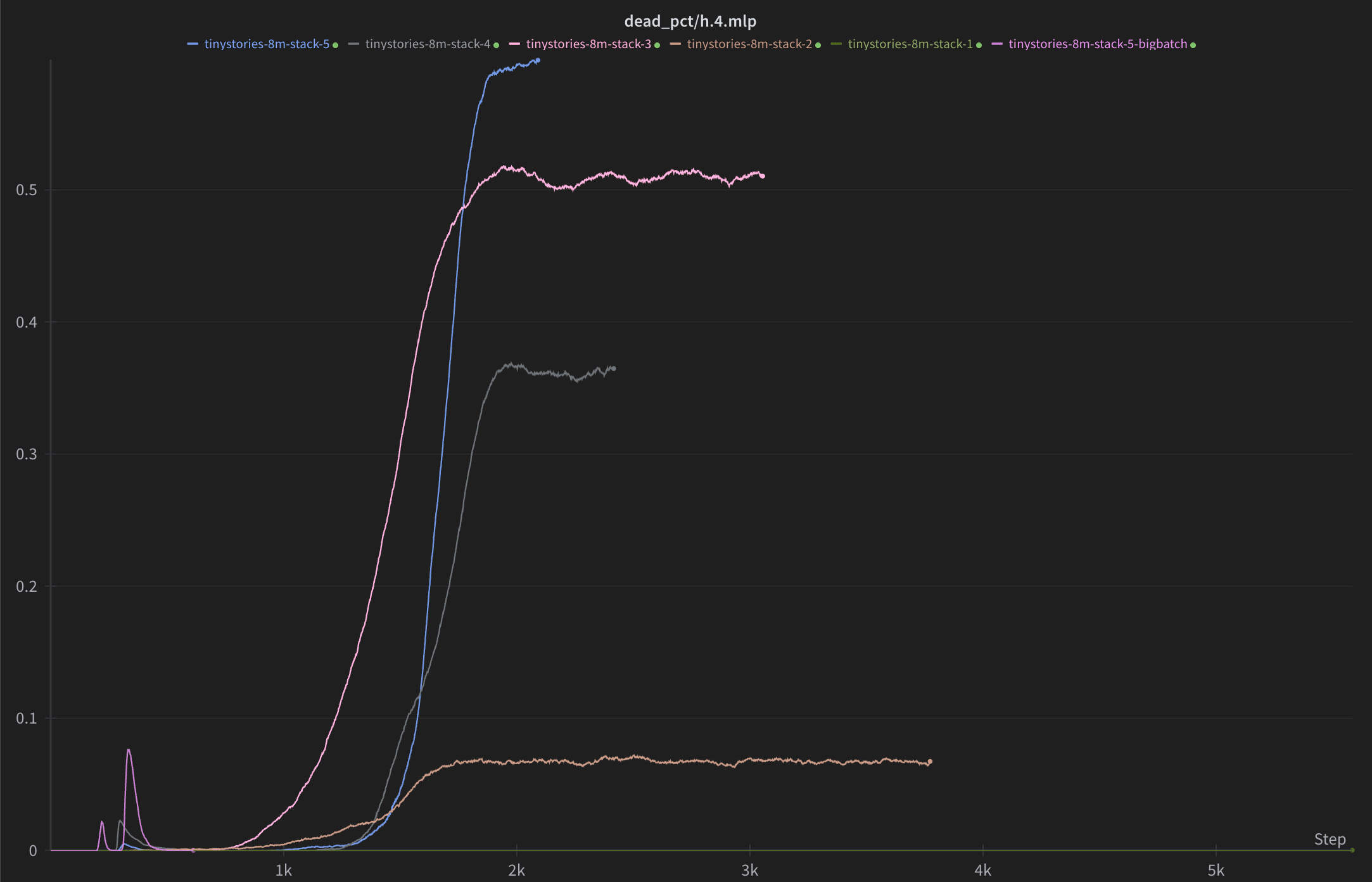
Dead neurons are a problem
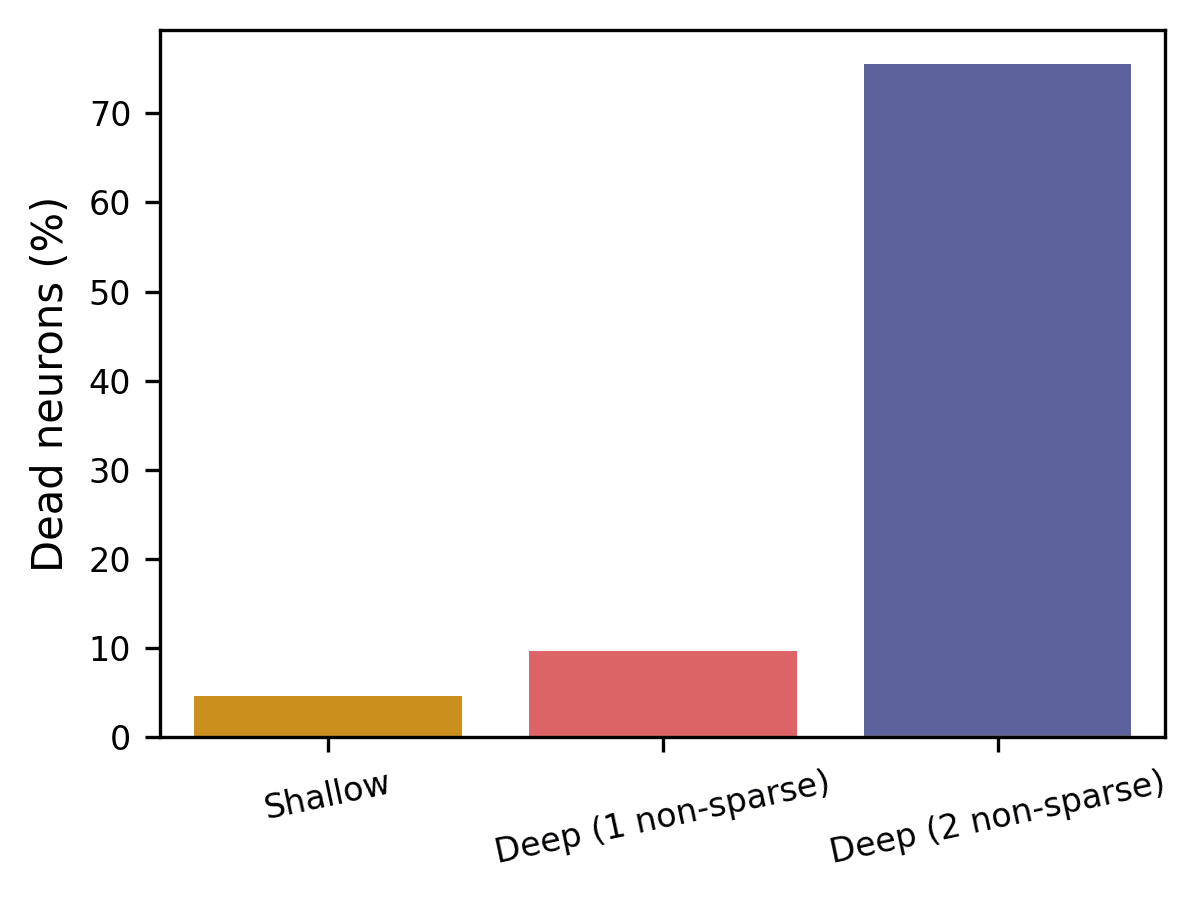
Increased SAE depth also tends to correspond to more dead features (Fig. 4), and this has been the biggest technical challenge in this project so far. I define a neuron as dead if it has not activated over the past 1.5 million inputs. I have a few new ideas for mitigating this issue that I’m optimistic about, but I wanted to share my work at this stage before investigating them.
Why is having dead neurons bad? For one, it will reduce your reconstruction accuracy. But also, this correlation between SAE depth and dead neuron frequency is a confounding factor in the interpretability analysis. For example, one of the reasons that I don’t make any claims about whether one SAE architecture is more interpretable than another is the vast difference in dead neurons between various architectures, and that the number of dead neurons almost certainly affects the automated interpretability score.
Deep SAE feature activation contexts
While difficult to present here, it’s also important to get a feel for these SAE features by looking at their activation contexts yourself. I’ve included examples of activation contexts for four features from the 1 non-sparse layer SAE for a taste of this (Fig. 5). These are sampled randomly from contexts on which the feature activates.

Conclusion
Why should you care?
I think that these results pretty strongly indicate that deep SAEs yield features which are on par with shallow SAEs in interpretability.
I also claim that conditioning on the success of SAEs being entirely explained by the accuracy of the superposition hypothesis implies a somewhat low probability of deep SAEs producing features that are interpretable at all. Like, if you have these clean linear features in your residual stream, and your single projection onto an overcomplete basis just effectively takes them out of superposition, wouldn’t adding more non-sparse layers just jumble them all up and reintroduce polysemanticity? From this perspective, these results support my original hypothesis that the theory of superposition does not fully explain the success of SAEs.
On the other hand, there is a story you could tell where this is still entirely linear feature superposition at work. Maybe, the non-sparse layers are just grouping together co-occurring linear features in the encoder and then ungrouping them in the decoder.
Either way, I think it is possible that adding more layers is a way to actually improve SAEs. Currently, it only seems like you can scale SAEs by making them wider, but maybe depth is also a dimension along which we can scale.
Edit (thanks to @Logan Riggs for bringing this up in the comments):
One of the major limitations of this approach is that the added nonlinearities obscure the relationship between deep SAE features and upstream / downstream mechanisms of the model. In the scenario where adding more layers to SAEs is actually useful, I think we would be giving up on this microscopic analysis, but also that this might be okay. For example, we can still examine where features activate and generate/verify human explanations for them. And the idea is that the extra layers would produce features that are increasingly meaningful/useful for this type of analysis.
Future directions
While my major claim in this post is that deep SAEs yield features which are as interpretable as shallow SAE features, I think it is plausible that controlling for the number of dead neurons would show that deep SAEs actually produce more interpretable features. The main technical challenge holding up this analysis of course is the reduction of dead neurons in deeper SAEs.
But also, I have several other directions for future investigation. For example:
- Are there consistent differences in the overall character of the features yielded by SAEs of increasing depth? For example, do deeper SAEs yield more abstract features?
- Would we see predictable changes in model behavior if we ablate deep SAE features?
- I think that the knee-jerk answer to this is no. But I also think the fact that deep SAEs are interpretable at all may question some of the assumptions that would lead to this answer. One way to look at this is that just as we can reason about linear features in the activation space of the model we are examining, perhaps we can just as easily reason about linear features in the activation space of the SAE, which I think would imply that ablations would yield predictable behavioral changes.
- How similar are the encoder and decoder of deep SAEs? For example, do we see any similarities that could indicate the grouping and ungrouping of linear features? Or are the encoder and decoder just distinct messes of weights?
Github
Automated interpretability score (fork)
Please reach out!
Above all, the reason I’m posting this work at its current stage is so that I can find people who may be interested in this work. Additionally, I’m new to mechanistic interpretability and alignment more generally, so I would greatly value receiving mentorship from someone more experienced. So, if you’re interested in collaboration, being a mentor, or just a chat, please do reach out to armaan.abraham@hotmail.com!
This is great. I'm a bit surprised you get such a big performance improvement from adding additional sparse layers; all of my experiments above have been adding non-sparse layers, but it looks like the MSE benefit you're getting with added sparse layers is in the same ballpark. You have certainly convinced me to try muon.
Another approach that I've (very recently) found quite effective in reducing the number of dead neurons with minimal MSE hit has been adding a small penalty term on the standard deviation of the encoder pre-act (i.e., before the top-k) means across the batch dimension. This has basically eliminated my dead neuron woes and this is what I'm currently running with. I'll probably try this in combination with muon sometime over the next couple of days.
And these ideas all sound great.