Authors: Senthooran Rajamanoharan*, Arthur Conmy*, Lewis Smith, Tom Lieberum, Vikrant Varma, János Kramár, Rohin Shah, Neel Nanda
A new paper from the Google DeepMind mech interp team: Improving Dictionary Learning with Gated Sparse Autoencoders!
Gated SAEs are a new Sparse Autoencoder architecture that seems to be a significant Pareto-improvement over normal SAEs, verified on models up to Gemma 7B. They are now our team's preferred way to train sparse autoencoders, and we'd love to see them adopted by the community! (Or to be convinced that it would be a bad idea for them to be adopted by the community!)

They achieve similar reconstruction with about half as many firing features, and while being either comparably or more interpretable (confidence interval for the increase is 0%-13%).
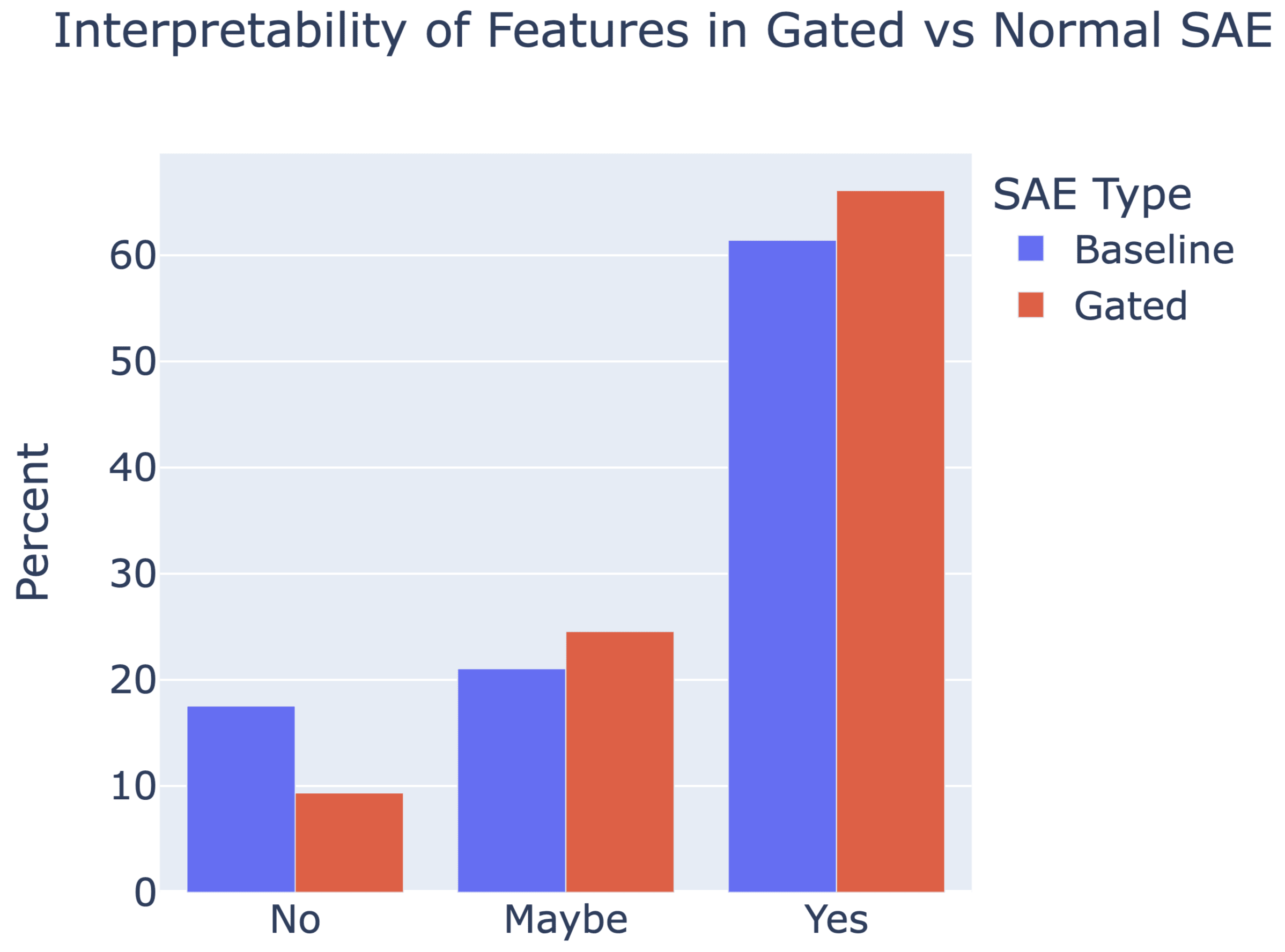
See Sen's Twitter summary, my Twitter summary, and the paper!
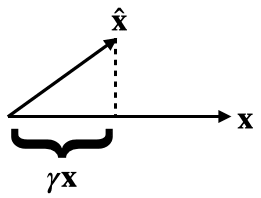

Oh, one other issue relating to this: in the paper it's claimed that if γ is the argmin of E[∥^x−γ′x∥22] then 1/γ is the argmin of E[∥γ′^x−x∥]. However, this is not actually true: the argmin of the latter expression is E[x⋅^x]E[∥^x∥22]≠(E[x⋅^x]E[∥x∥2])−1. To get an intuition here, consider the case where ^x and x are very nearly perpendicular, with the angle between them just slightly less than 90∘. Then you should be able to convince yourself that the best factor to scale either x or ^x by in order to minimize the distance to the other will be just slightly greater than 0. Thus the optimal scaling factors cannot be reciprocals of each other.
ETA: Thinking on this a bit more, this might actually reflect a general issue with the way we think about feature shrinkage; namely, that whenever there is a nonzero angle between two vectors of the same length, the best way to make either vector close to the other will be by shrinking it. I'll need to think about whether this makes me less convinced that the usual measures of feature shrinkage are capturing a real thing.
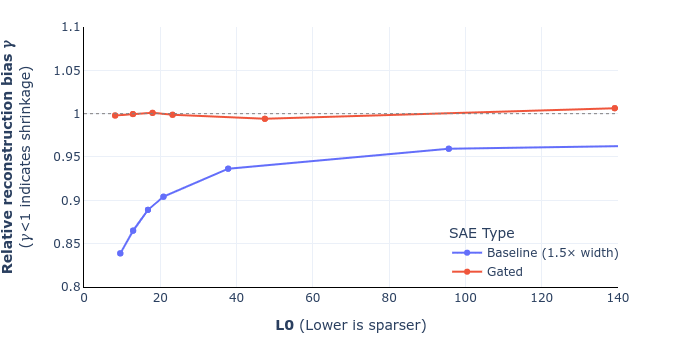
ETA2: In fact, now I'm a bit confused why your figure 6 shows no shrinkage. Based on what I wrote above in this comment, we should generally expect to see shrinkage (according to the definition given in equation (9)) whenever the autoencoder isn't perfect. I guess the answer must somehow be "equation (10) actually is a good measure of shrinkage, in fact a better measure of shrinkage than the 'corrected' version of equation (10)." That's pretty cool and surprising, because I don't really have a great intuition for what equation (10) is actually capturing.